Sample Efficient Reinforcement Learning from Human Feedback via Active Exploration

Preference-based feedback is important for many applications in reinforcement learning where direct evaluation of a reward function is not feasible. A notable recent example arises in reinforcement learning from human feedback (RLHF) on large language models. For many applications of RLHF, the cost of acquiring the human feedback can be substantial. In this work, we take advantage of the fact that one can often choose contexts at which to obtain human feedback in order to most efficiently identify a good policy, and formalize this as an offline contextual dueling bandit problem. We give an upper-confidence-bound style algorithm for this problem and prove a polynomial worst-case regret bound. We then provide empirical confirmation in a synthetic setting that our approach outperforms existing methods. After, we extend the setting and methodology for practical use in RLHF training of large language models. Here, our method is able to reach better performance with fewer samples of human preferences than multiple baselines on three real-world datasets.

REDUCR: Robust Data Downsampling Using Class Priority Reweighting

Modern machine learning models are becoming increasingly expensive to train for real-world image and text classification tasks, where massive web-scale data is collected in a streaming fashion. To reduce the training cost, online batch selection techniques have been developed to choose the most informative datapoints. However, these techniques can suffer from poor worst-class generalization performance due to class imbalance and distributional shifts. This work introduces REDUCR, a robust and efficient data downsampling method that uses class priority reweighting. REDUCR reduces the training data while preserving worst-class generalization performance. REDUCR assigns priority weights to datapoints in a class-aware manner using an online learning algorithm. We demonstrate the data efficiency and robust performance of REDUCR on vision and text classification tasks. On web-scraped datasets with imbalanced class distributions, REDUCR significantly improves worst-class test accuracy (and average accuracy), surpassing state-of-the-art methods by around 15%.

Robust Best-arm Identification in Linear Bandits

We study the robust best-arm identification problem (RBAI) in the case of linear rewards. The primary objective is to identify a near-optimal robust arm, which involves selecting arms at every round and assessing their robustness by exploring potential adversarial actions. This approach is particularly relevant when utilizing a simulator and seeking to identify a robust solution for real-world transfer. To this end, we present an instance-dependent lower bound for the robust best-arm identification problem with linear rewards. Furthermore, we propose both static and adaptive bandit algorithms that achieve sample complexity that matches the lower bound. In synthetic experiments, our algorithms effectively identify the best robust arm and perform similarly to the oracle strategy. As an application, we examine diabetes care and the process of learning insulin dose recommendations that are robust with respect to inaccuracies in standard calculators. Our algorithms prove to be effective in identifying robust dosage values across various age ranges of patients.

Distributionally Robust Model-based Reinforcement Learning with Large State Spaces

Three major challenges in reinforcement learning are the complex dynamical systems with large state spaces, the costly data acquisition processes, and the deviation of real-world dynamics from the training environment deployment. To overcome these issues, we study distributionally robust Markov decision processes with continuous state spaces under the widely used Kullback-Leibler, chi-square, and total variation uncertainty sets. We propose a model-based approach that utilizes Gaussian Processes and the maximum variance reduction algorithm to efficiently learn multi-output nominal transition dynamics, leveraging access to a generative model (i.e., simulator). We further demonstrate the statistical sample complexity of the proposed method for different uncertainty sets. These complexity bounds are independent of the number of states and extend beyond linear dynamics, ensuring the effectiveness of our approach in identifying near-optimal distributionally-robust policies. The proposed method can be further combined with other model-free distributionally robust reinforcement learning methods to obtain a near-optimal robust policy. Experimental results demonstrate the robustness of our algorithm to distributional shifts and its superior performance in terms of the number of samples needed.

Safe Model-Based Multi-Agent Mean-Field Reinforcement Learning

Many applications, e.g., in shared mobility, require coordinating a large number of agents. Mean-field reinforcement learning addresses the resulting scalability challenge by optimizing the policy of a representative agent. In this paper, we address an important generalization where there exist global constraints on the distribution of agents (e.g., requiring capacity constraints or minimum coverage requirements to be met). We propose Safe-$\text{M}^3$-UCRL, the first model-based algorithm that attains safe policies even in the case of unknown transition dynamics. As a key ingredient, it uses epistemic uncertainty in the transition model within a log-barrier approach to ensure pessimistic constraints satisfaction with high probability. We showcase Safe-$\text{M}^3$-UCRL on the vehicle repositioning problem faced by many shared mobility operators and evaluate its performance through simulations built on Shenzhen taxi trajectory data. Our algorithm effectively meets the demand in critical areas while ensuring service accessibility in regions with low demand.

Efficient Planning in Combinatorial Action Spaces with Applications to Cooperative Multi-Agent Reinforcement Learning

A practical challenge in reinforcement learning are combinatorial action spaces that make planning computationally demanding. For example, in cooperative multi-agent reinforcement learning, a potentially large number of agents jointly optimize a global reward function, which leads to a combinatorial blow-up in the action space by the number of agents. As a minimal requirement, we assume access to an argmax oracle that allows to efficiently compute the greedy policy for any Q-function in the model class. Building on recent work in planning with local access to a simulator and linear function approximation, we propose efficient algorithms for this setting that lead to polynomial compute and query complexity in all relevant problem parameters. For the special case where the feature decomposition is additive, we further improve the bounds and extend the results to the kernelized setting with an efficient algorithm.

Near-optimal Policy Identification in Active Reinforcement Learning

Many real-world reinforcement learning tasks require control of complex dynamical systems that involve both costly data acquisition processes and large state spaces. In cases where the transition dynamics can be readily evaluated at specified states (e.g., via a simulator), agents can operate in what is often referred to as planning with a \emph{generative model}. We propose the AE-LSVI algorithm for best-policy identification, a novel variant of the kernelized least-squares value iteration (LSVI) algorithm that combines optimism with pessimism for active exploration (AE). AE-LSVI provably identifies a near-optimal policy \emph{uniformly} over an entire state space and achieves polynomial sample complexity guarantees that are independent of the number of states. When specialized to the recently introduced offline contextual Bayesian optimization setting, our algorithm achieves improved sample complexity bounds. Experimentally, we demonstrate that AE-LSVI outperforms other RL algorithms in a variety of environments when robustness to the initial state is required.

Movement Penalized Bayesian Optimization with Application to Wind Energy Systems

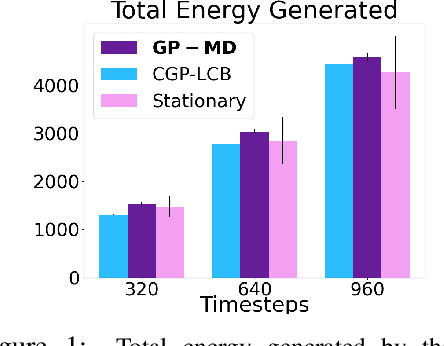
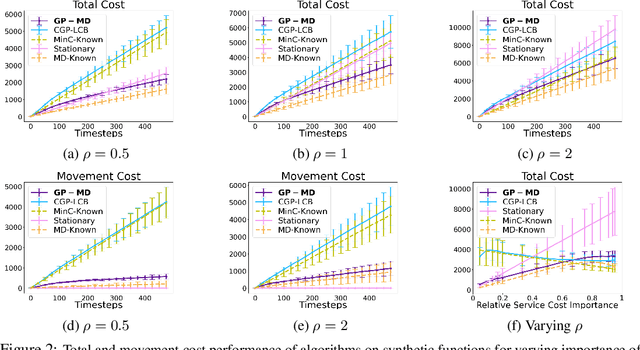
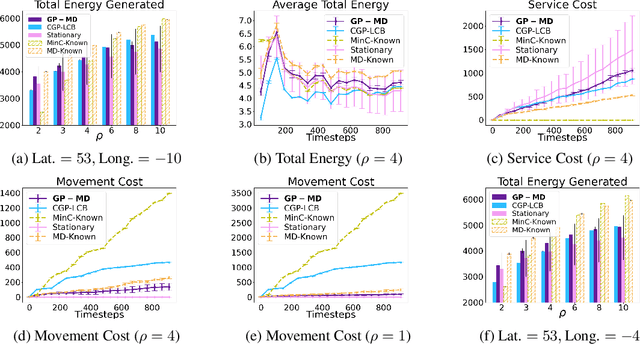
Contextual Bayesian optimization (CBO) is a powerful framework for sequential decision-making given side information, with important applications, e.g., in wind energy systems. In this setting, the learner receives context (e.g., weather conditions) at each round, and has to choose an action (e.g., turbine parameters). Standard algorithms assume no cost for switching their decisions at every round. However, in many practical applications, there is a cost associated with such changes, which should be minimized. We introduce the episodic CBO with movement costs problem and, based on the online learning approach for metrical task systems of Coester and Lee (2019), propose a novel randomized mirror descent algorithm that makes use of Gaussian Process confidence bounds. We compare its performance with the offline optimal sequence for each episode and provide rigorous regret guarantees. We further demonstrate our approach on the important real-world application of altitude optimization for Airborne Wind Energy Systems. In the presence of substantial movement costs, our algorithm consistently outperforms standard CBO algorithms.

Graph Neural Network Bandits

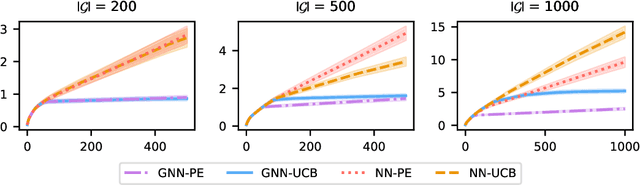
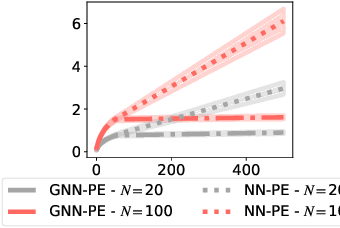
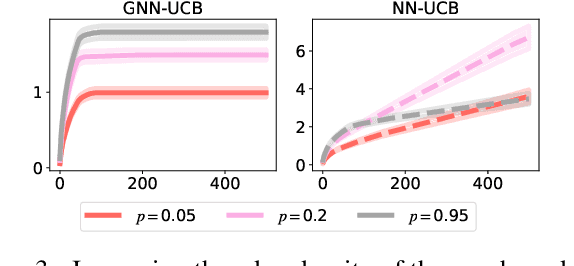
We consider the bandit optimization problem with the reward function defined over graph-structured data. This problem has important applications in molecule design and drug discovery, where the reward is naturally invariant to graph permutations. The key challenges in this setting are scaling to large domains, and to graphs with many nodes. We resolve these challenges by embedding the permutation invariance into our model. In particular, we show that graph neural networks (GNNs) can be used to estimate the reward function, assuming it resides in the Reproducing Kernel Hilbert Space of a permutation-invariant additive kernel. By establishing a novel connection between such kernels and the graph neural tangent kernel (GNTK), we introduce the first GNN confidence bound and use it to design a phased-elimination algorithm with sublinear regret. Our regret bound depends on the GNTK's maximum information gain, which we also provide a bound for. While the reward function depends on all $N$ node features, our guarantees are independent of the number of graph nodes $N$. Empirically, our approach exhibits competitive performance and scales well on graph-structured domains.

A Robust Phased Elimination Algorithm for Corruption-Tolerant Gaussian Process Bandits

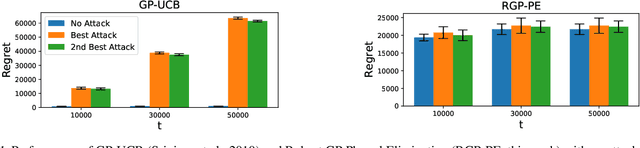
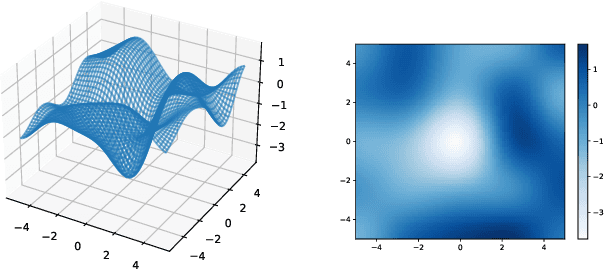
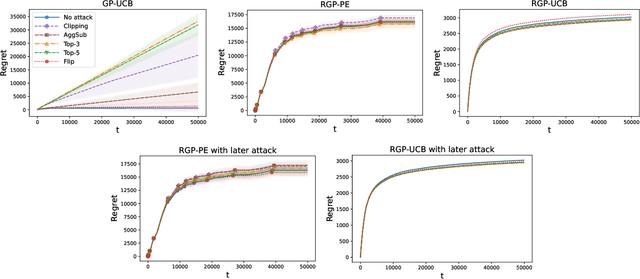
We consider the sequential optimization of an unknown, continuous, and expensive to evaluate reward function, from noisy and adversarially corrupted observed rewards. When the corruption attacks are subject to a suitable budget $C$ and the function lives in a Reproducing Kernel Hilbert Space (RKHS), the problem can be posed as corrupted Gaussian process (GP) bandit optimization. We propose a novel robust elimination-type algorithm that runs in epochs, combines exploration with infrequent switching to select a small subset of actions, and plays each action for multiple time instants. Our algorithm, Robust GP Phased Elimination (RGP-PE), successfully balances robustness to corruptions with exploration and exploitation such that its performance degrades minimally in the presence (or absence) of adversarial corruptions. When $T$ is the number of samples and $\gamma_T$ is the maximal information gain, the corruption-dependent term in our regret bound is $O(C \gamma_T^{3/2})$, which is significantly tighter than the existing $O(C \sqrt{T \gamma_T})$ for several commonly-considered kernels. We perform the first empirical study of robustness in the corrupted GP bandit setting, and show that our algorithm is robust against a variety of adversarial attacks.