Bandits with Preference Feedback: A Stackelberg Game Perspective

Bandits with preference feedback present a powerful tool for optimizing unknown target functions when only pairwise comparisons are allowed instead of direct value queries. This model allows for incorporating human feedback into online inference and optimization and has been employed in systems for fine-tuning large language models. The problem is well understood in simplified settings with linear target functions or over finite small domains that limit practical interest. Taking the next step, we consider infinite domains and nonlinear (kernelized) rewards. In this setting, selecting a pair of actions is quite challenging and requires balancing exploration and exploitation at two levels: within the pair, and along the iterations of the algorithm. We propose MAXMINLCB, which emulates this trade-off as a zero-sum Stackelberg game, and chooses action pairs that are informative and yield favorable rewards. MAXMINLCB consistently outperforms existing algorithms and satisfies an anytime-valid rate-optimal regret guarantee. This is due to our novel preference-based confidence sequences for kernelized logistic estimators.

Progressive Entropic Optimal Transport Solvers

Optimal transport (OT) has profoundly impacted machine learning by providing theoretical and computational tools to realign datasets. In this context, given two large point clouds of sizes $n$ and $m$ in $\mathbb{R}^d$, entropic OT (EOT) solvers have emerged as the most reliable tool to either solve the Kantorovich problem and output a $n\times m$ coupling matrix, or to solve the Monge problem and learn a vector-valued push-forward map. While the robustness of EOT couplings/maps makes them a go-to choice in practical applications, EOT solvers remain difficult to tune because of a small but influential set of hyperparameters, notably the omnipresent entropic regularization strength $\varepsilon$. Setting $\varepsilon$ can be difficult, as it simultaneously impacts various performance metrics, such as compute speed, statistical performance, generalization, and bias. In this work, we propose a new class of EOT solvers (ProgOT), that can estimate both plans and transport maps. We take advantage of several opportunities to optimize the computation of EOT solutions by dividing mass displacement using a time discretization, borrowing inspiration from dynamic OT formulations, and conquering each of these steps using EOT with properly scheduled parameters. We provide experimental evidence demonstrating that ProgOT is a faster and more robust alternative to standard solvers when computing couplings at large scales, even outperforming neural network-based approaches. We also prove statistical consistency of our approach for estimating optimal transport maps.

Anytime Model Selection in Linear Bandits

Model selection in the context of bandit optimization is a challenging problem, as it requires balancing exploration and exploitation not only for action selection, but also for model selection. One natural approach is to rely on online learning algorithms that treat different models as experts. Existing methods, however, scale poorly ($\text{poly}M$) with the number of models $M$ in terms of their regret. Our key insight is that, for model selection in linear bandits, we can emulate full-information feedback to the online learner with a favorable bias-variance trade-off. This allows us to develop ALEXP, which has an exponentially improved ($\log M$) dependence on $M$ for its regret. ALEXP has anytime guarantees on its regret, and neither requires knowledge of the horizon $n$, nor relies on an initial purely exploratory stage. Our approach utilizes a novel time-uniform analysis of the Lasso, establishing a new connection between online learning and high-dimensional statistics.

Hallucinated Adversarial Control for Conservative Offline Policy Evaluation

We study the problem of conservative off-policy evaluation (COPE) where given an offline dataset of environment interactions, collected by other agents, we seek to obtain a (tight) lower bound on a policy's performance. This is crucial when deciding whether a given policy satisfies certain minimal performance/safety criteria before it can be deployed in the real world. To this end, we introduce HAMBO, which builds on an uncertainty-aware learned model of the transition dynamics. To form a conservative estimate of the policy's performance, HAMBO hallucinates worst-case trajectories that the policy may take, within the margin of the models' epistemic confidence regions. We prove that the resulting COPE estimates are valid lower bounds, and, under regularity conditions, show their convergence to the true expected return. Finally, we discuss scalable variants of our approach based on Bayesian Neural Networks and empirically demonstrate that they yield reliable and tight lower bounds in various continuous control environments.

Instance-Dependent Generalization Bounds via Optimal Transport

Existing generalization bounds fail to explain crucial factors that drive generalization of modern neural networks. Since such bounds often hold uniformly over all parameters, they suffer from over-parametrization, and fail to account for the strong inductive bias of initialization and stochastic gradient descent. As an alternative, we propose a novel optimal transport interpretation of the generalization problem. This allows us to derive instance-dependent generalization bounds that depend on the local Lipschitz regularity of the earned prediction function in the data space. Therefore, our bounds are agnostic to the parametrization of the model and work well when the number of training samples is much smaller than the number of parameters. With small modifications, our approach yields accelerated rates for data on low-dimensional manifolds, and guarantees under distribution shifts. We empirically analyze our generalization bounds for neural networks, showing that the bound values are meaningful and capture the effect of popular regularization methods during training.

Lifelong Bandit Optimization: No Prior and No Regret

In practical applications, machine learning algorithms are often repeatedly applied to problems with similar structure over and over again. We focus on solving a sequence of bandit optimization tasks and develop LiBO, an algorithm which adapts to the environment by learning from past experience and becoming more sample-efficient in the process. We assume a kernelized structure where the kernel is unknown but shared across all tasks. LiBO sequentially meta-learns a kernel that approximates the true kernel and simultaneously solves the incoming tasks with the latest kernel estimate. Our algorithm can be paired with any kernelized bandit algorithm and guarantees oracle optimal performance, meaning that as more tasks are solved, the regret of LiBO on each task converges to the regret of the bandit algorithm with oracle knowledge of the true kernel. Naturally, if paired with a sublinear bandit algorithm, LiBO yields a sublinear lifelong regret. We also show that direct access to the data from each task is not necessary for attaining sublinear regret. The lifelong problem can thus be solved in a federated manner, while keeping the data of each task private.

Graph Neural Network Bandits

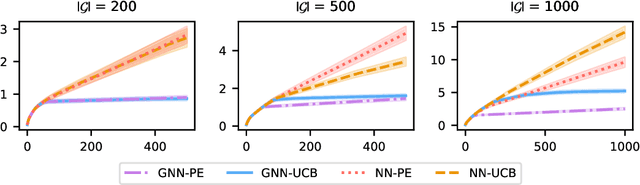
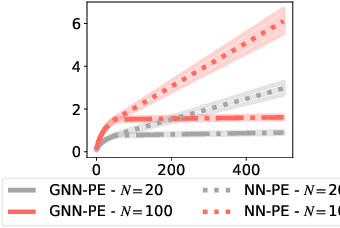
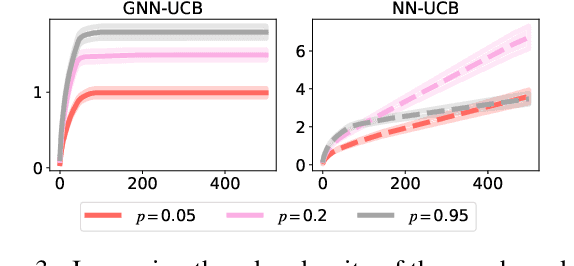
We consider the bandit optimization problem with the reward function defined over graph-structured data. This problem has important applications in molecule design and drug discovery, where the reward is naturally invariant to graph permutations. The key challenges in this setting are scaling to large domains, and to graphs with many nodes. We resolve these challenges by embedding the permutation invariance into our model. In particular, we show that graph neural networks (GNNs) can be used to estimate the reward function, assuming it resides in the Reproducing Kernel Hilbert Space of a permutation-invariant additive kernel. By establishing a novel connection between such kernels and the graph neural tangent kernel (GNTK), we introduce the first GNN confidence bound and use it to design a phased-elimination algorithm with sublinear regret. Our regret bound depends on the GNTK's maximum information gain, which we also provide a bound for. While the reward function depends on all $N$ node features, our guarantees are independent of the number of graph nodes $N$. Empirically, our approach exhibits competitive performance and scales well on graph-structured domains.

Meta-Learning Hypothesis Spaces for Sequential Decision-making

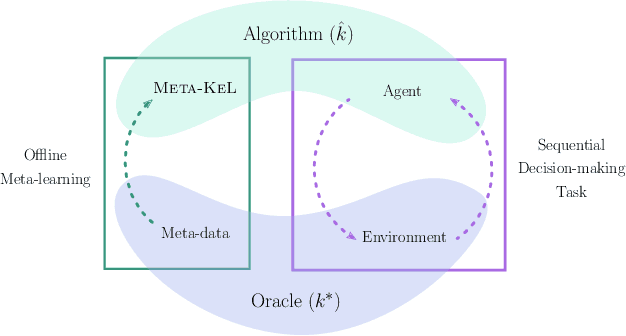
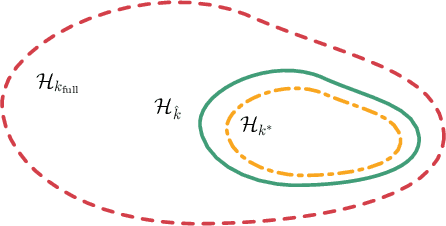
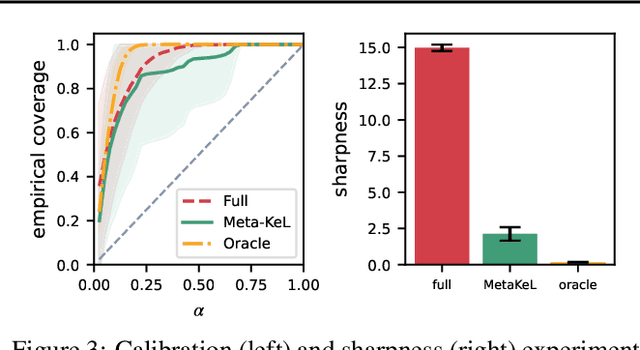
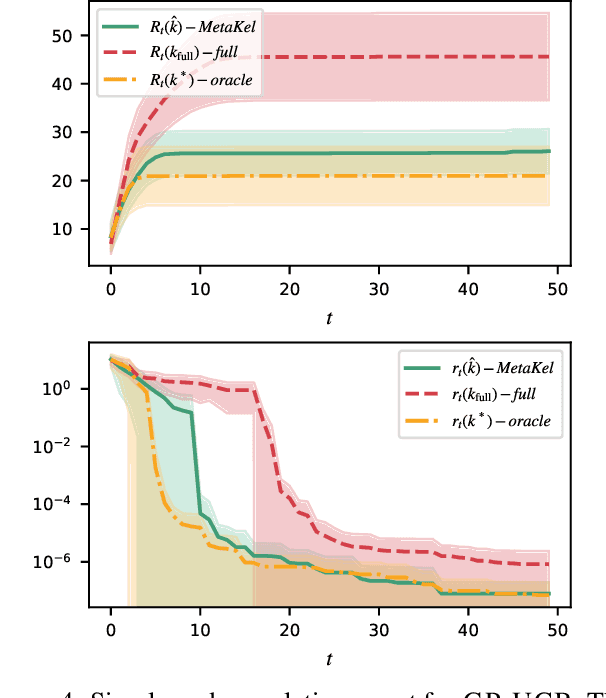
Obtaining reliable, adaptive confidence sets for prediction functions (hypotheses) is a central challenge in sequential decision-making tasks, such as bandits and model-based reinforcement learning. These confidence sets typically rely on prior assumptions on the hypothesis space, e.g., the known kernel of a Reproducing Kernel Hilbert Space (RKHS). Hand-designing such kernels is error prone, and misspecification may lead to poor or unsafe performance. In this work, we propose to meta-learn a kernel from offline data (Meta-KeL). For the case where the unknown kernel is a combination of known base kernels, we develop an estimator based on structured sparsity. Under mild conditions, we guarantee that our estimated RKHS yields valid confidence sets that, with increasing amounts of offline data, become as tight as those given the true unknown kernel. We demonstrate our approach on the kernelized bandit problem (a.k.a.~Bayesian optimization), where we establish regret bounds competitive with those given the true kernel. We also empirically evaluate the effectiveness of our approach on a Bayesian optimization task.

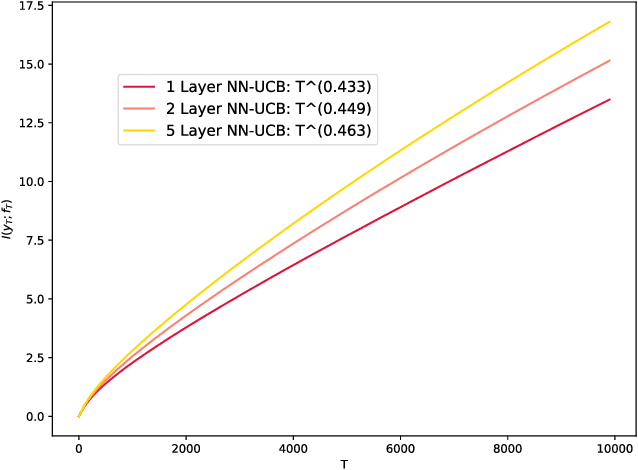
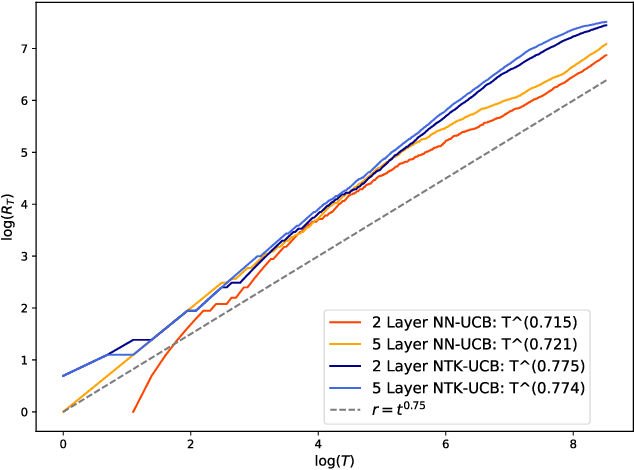
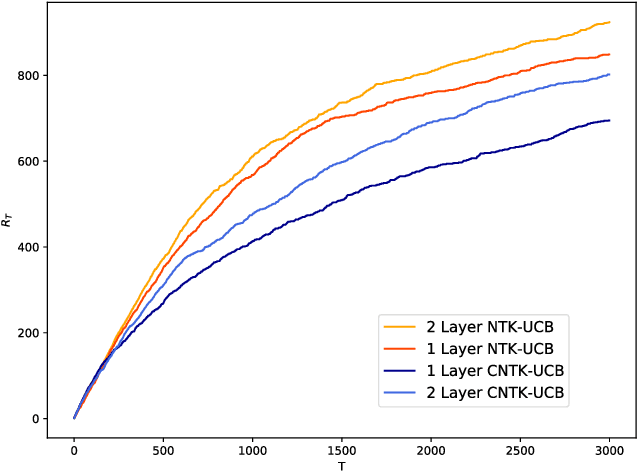
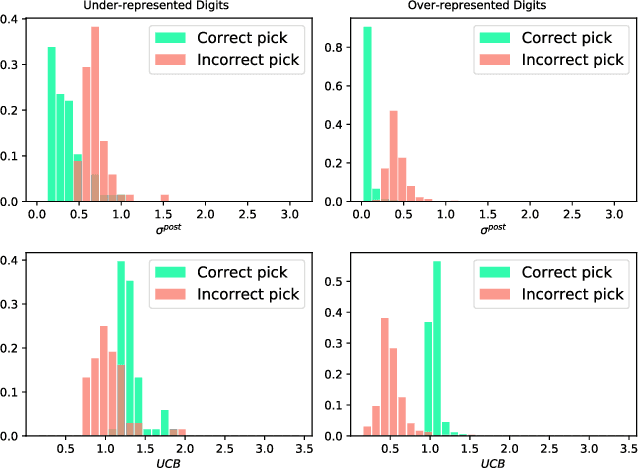
Neural Contextual Bandits without Regret

Contextual bandits are a rich model for sequential decision making given side information, with important applications, e.g., in recommender systems. We propose novel algorithms for contextual bandits harnessing neural networks to approximate the unknown reward function. We resolve the open problem of proving sublinear regret bounds in this setting for general context sequences, considering both fully-connected and convolutional networks. To this end, we first analyze NTK-UCB, a kernelized bandit optimization algorithm employing the Neural Tangent Kernel (NTK), and bound its regret in terms of the NTK maximum information gain $\gamma_T$, a complexity parameter capturing the difficulty of learning. Our bounds on $\gamma_T$ for the NTK may be of independent interest. We then introduce our neural network based algorithm NN-UCB, and show that its regret closely tracks that of NTK-UCB. Under broad non-parametric assumptions about the reward function, our approach converges to the optimal policy at a $\tilde{\mathcal{O}}(T^{-1/2d})$ rate, where $d$ is the dimension of the context.