Puzzle: Distillation-Based NAS for Inference-Optimized LLMs

Large language models (LLMs) have demonstrated remarkable capabilities, but their adoption is limited by high computational costs during inference. While increasing parameter counts enhances accuracy, it also widens the gap between state-of-the-art capabilities and practical deployability. We present Puzzle, a framework to accelerate LLM inference on specific hardware while preserving their capabilities. Through an innovative application of neural architecture search (NAS) at an unprecedented scale, Puzzle systematically optimizes models with tens of billions of parameters under hardware constraints. Our approach utilizes blockwise local knowledge distillation (BLD) for parallel architecture exploration and employs mixed-integer programming for precise constraint optimization. We demonstrate the real-world impact of our framework through Llama-3.1-Nemotron-51B-Instruct (Nemotron-51B), a publicly available model derived from Llama-3.1-70B-Instruct. Nemotron-51B achieves a 2.17x inference throughput speedup, fitting on a single NVIDIA H100 GPU while preserving 98.4% of the original model's capabilities. Nemotron-51B currently stands as the most accurate language model capable of inference on a single GPU with large batch sizes. Remarkably, this transformation required just 45B training tokens, compared to over 15T tokens used for the 70B model it was derived from. This establishes a new paradigm where powerful models can be optimized for efficient deployment with only negligible compromise of their capabilities, demonstrating that inference performance, not parameter count alone, should guide model selection. With the release of Nemotron-51B and the presentation of the Puzzle framework, we provide practitioners immediate access to state-of-the-art language modeling capabilities at significantly reduced computational costs.

D-Flow: Differentiating through Flows for Controlled Generation

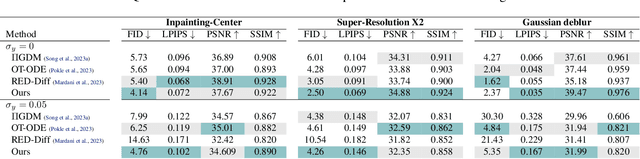
Taming the generation outcome of state of the art Diffusion and Flow-Matching (FM) models without having to re-train a task-specific model unlocks a powerful tool for solving inverse problems, conditional generation, and controlled generation in general. In this work we introduce D-Flow, a simple framework for controlling the generation process by differentiating through the flow, optimizing for the source (noise) point. We motivate this framework by our key observation stating that for Diffusion/FM models trained with Gaussian probability paths, differentiating through the generation process projects gradient on the data manifold, implicitly injecting the prior into the optimization process. We validate our framework on linear and non-linear controlled generation problems including: image and audio inverse problems and conditional molecule generation reaching state of the art performance across all.

Mosaic-SDF for 3D Generative Models

Current diffusion or flow-based generative models for 3D shapes divide to two: distilling pre-trained 2D image diffusion models, and training directly on 3D shapes. When training a diffusion or flow models on 3D shapes a crucial design choice is the shape representation. An effective shape representation needs to adhere three design principles: it should allow an efficient conversion of large 3D datasets to the representation form; it should provide a good tradeoff of approximation power versus number of parameters; and it should have a simple tensorial form that is compatible with existing powerful neural architectures. While standard 3D shape representations such as volumetric grids and point clouds do not adhere to all these principles simultaneously, we advocate in this paper a new representation that does. We introduce Mosaic-SDF (M-SDF): a simple 3D shape representation that approximates the Signed Distance Function (SDF) of a given shape by using a set of local grids spread near the shape's boundary. The M-SDF representation is fast to compute for each shape individually making it readily parallelizable; it is parameter efficient as it only covers the space around the shape's boundary; and it has a simple matrix form, compatible with Transformer-based architectures. We demonstrate the efficacy of the M-SDF representation by using it to train a 3D generative flow model including class-conditioned generation with the 3D Warehouse dataset, and text-to-3D generation using a dataset of about 600k caption-shape pairs.

Equivariant Polynomials for Graph Neural Networks

Graph Neural Networks (GNN) are inherently limited in their expressive power. Recent seminal works (Xu et al., 2019; Morris et al., 2019b) introduced the Weisfeiler-Lehman (WL) hierarchy as a measure of expressive power. Although this hierarchy has propelled significant advances in GNN analysis and architecture developments, it suffers from several significant limitations. These include a complex definition that lacks direct guidance for model improvement and a WL hierarchy that is too coarse to study current GNNs. This paper introduces an alternative expressive power hierarchy based on the ability of GNNs to calculate equivariant polynomials of a certain degree. As a first step, we provide a full characterization of all equivariant graph polynomials by introducing a concrete basis, significantly generalizing previous results. Each basis element corresponds to a specific multi-graph, and its computation over some graph data input corresponds to a tensor contraction problem. Second, we propose algorithmic tools for evaluating the expressiveness of GNNs using tensor contraction sequences, and calculate the expressive power of popular GNNs. Finally, we enhance the expressivity of common GNN architectures by adding polynomial features or additional operations / aggregations inspired by our theory. These enhanced GNNs demonstrate state-of-the-art results in experiments across multiple graph learning benchmarks.

Frame Averaging for Invariant and Equivariant Network Design

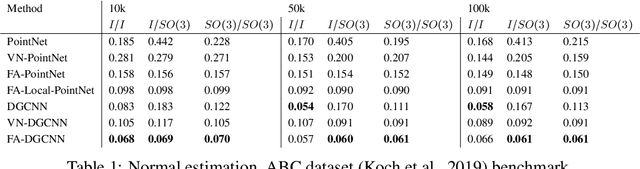
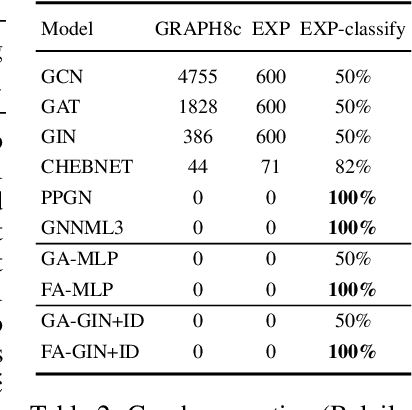
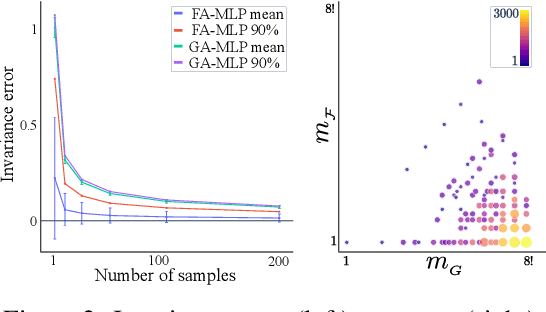
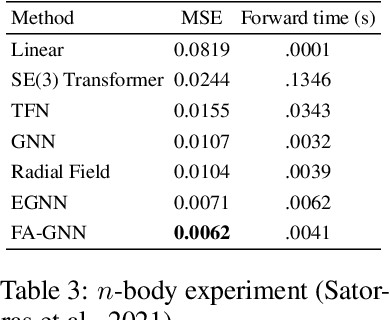
Many machine learning tasks involve learning functions that are known to be invariant or equivariant to certain symmetries of the input data. However, it is often challenging to design neural network architectures that respect these symmetries while being expressive and computationally efficient. For example, Euclidean motion invariant/equivariant graph or point cloud neural networks. We introduce Frame Averaging (FA), a general purpose and systematic framework for adapting known (backbone) architectures to become invariant or equivariant to new symmetry types. Our framework builds on the well known group averaging operator that guarantees invariance or equivariance but is intractable. In contrast, we observe that for many important classes of symmetries, this operator can be replaced with an averaging operator over a small subset of the group elements, called a frame. We show that averaging over a frame guarantees exact invariance or equivariance while often being much simpler to compute than averaging over the entire group. Furthermore, we prove that FA-based models have maximal expressive power in a broad setting and in general preserve the expressive power of their backbone architectures. Using frame averaging, we propose a new class of universal Graph Neural Networks (GNNs), universal Euclidean motion invariant point cloud networks, and Euclidean motion invariant Message Passing (MP) GNNs. We demonstrate the practical effectiveness of FA on several applications including point cloud normal estimation, beyond $2$-WL graph separation, and $n$-body dynamics prediction, achieving state-of-the-art results in all of these benchmarks.

From Graph Low-Rank Global Attention to 2-FWL Approximation

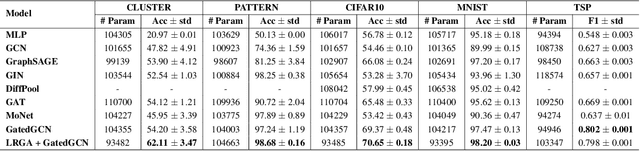
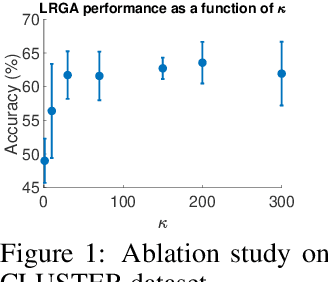
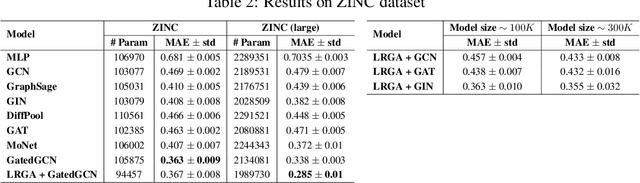
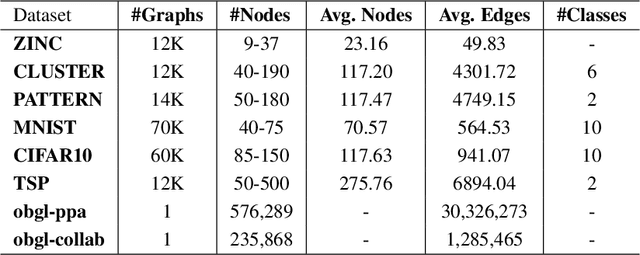
Graph Neural Networks (GNNs) are known to have an expressive power bounded by that of the vertex coloring algorithm (Xu et al., 2019a; Morris et al., 2018). However, for rich node features, such a bound does not exist and GNNs can be shown to be universal, namely, have the theoretical ability to approximate arbitrary graph functions. It is well known, however, that expressive power alone does not imply good generalization. In an effort to improve generalization of GNNs we suggest the Low-Rank Global Attention (LRGA) module, taking advantage of the efficiency of low rank matrix-vector multiplication, that improves the algorithmic alignment (Xu et al., 2019b) of GNNs with the 2-folklore Weisfeiler-Lehman (FWL) algorithm; 2-FWL is a graph isomorphism algorithm that is strictly more powerful than vertex coloring. Concretely, we: (i) formulate 2-FWL using polynomial kernels; (ii) show LRGA aligns with this 2-FWL formulation; and (iii) bound the sample complexity of the kernel's feature map when learned with a randomly initialized two-layer MLP. The latter means the generalization error can be made arbitrarily small when training LRGA to learn the 2-FWL algorithm. From a practical point of view, augmenting existing GNN layers with LRGA produces state of the art results on most datasets in a GNN standard benchmark.