Technical Report: Scalable Active Information Acquisition for Multi-Robot Systems

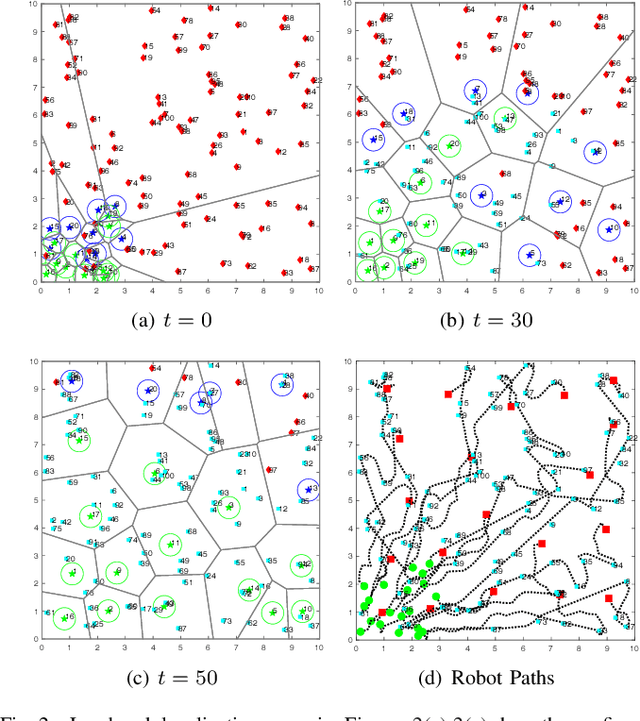
This paper proposes a novel highly scalable non-myopic planning algorithm for multi-robot Active Information Acquisition (AIA) tasks. AIA scenarios include target localization and tracking, active SLAM, surveillance, environmental monitoring and others. The objective is to compute control policies for multiple robots which minimize the accumulated uncertainty of a static hidden state over an a priori unknown horizon. The majority of existing AIA approaches are centralized and, therefore, face scaling challenges. To mitigate this issue, we propose an online algorithm that relies on decomposing the AIA task into local tasks via a dynamic space-partitioning method. The local subtasks are formulated online and require the robots to switch between exploration and active information gathering roles depending on their functionality in the environment. The switching process is tightly integrated with optimizing information gathering giving rise to a hybrid control approach. We show that the proposed decomposition-based algorithm is probabilistically complete for homogeneous sensor teams and under linearity and Gaussian assumptions. We provide extensive simulation results that show that the proposed algorithm can address large-scale estimation tasks that are computationally challenging to solve using existing centralized approaches.

Model-Based Domain Generalization

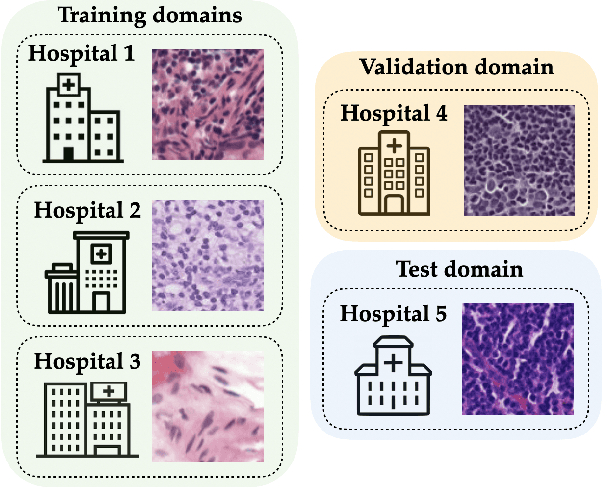
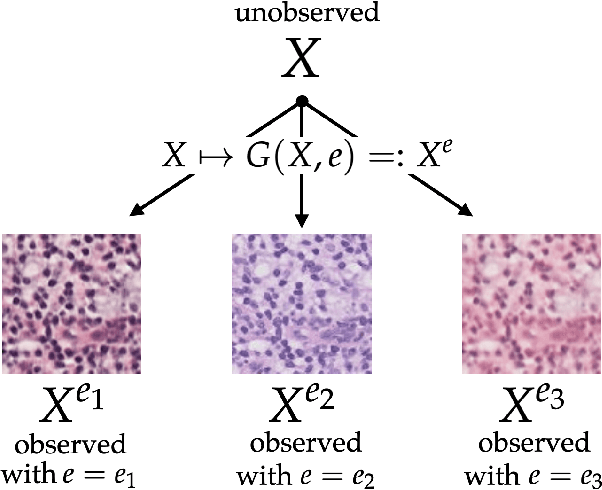
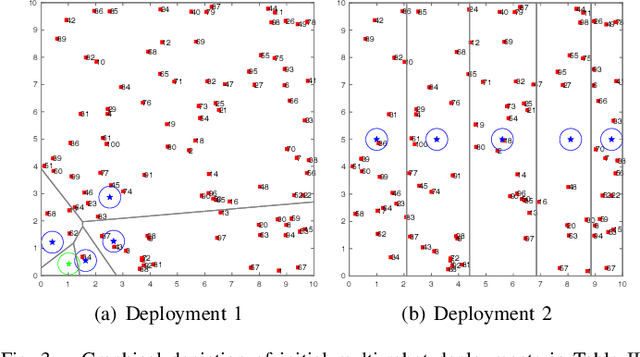
We consider the problem of domain generalization, in which a predictor is trained on data drawn from a family of related training domains and tested on a distinct and unseen test domain. While a variety of approaches have been proposed for this setting, it was recently shown that no existing algorithm can consistently outperform empirical risk minimization (ERM) over the training domains. To this end, in this paper we propose a novel approach for the domain generalization problem called Model-Based Domain Generalization. In our approach, we first use unlabeled data from the training domains to learn multi-modal domain transformation models that map data from one training domain to any other domain. Next, we propose a constrained optimization-based formulation for domain generalization which enforces that a trained predictor be invariant to distributional shifts under the underlying domain transformation model. Finally, we propose a novel algorithmic framework for efficiently solving this constrained optimization problem. In our experiments, we show that this approach outperforms both ERM and domain generalization algorithms on numerous well-known, challenging datasets, including WILDS, PACS, and ImageNet. In particular, our algorithms beat the current state-of-the-art methods on the very-recently-proposed WILDS benchmark by up to 20 percentage points.

Achieving Linear Convergence in Federated Learning under Objective and Systems Heterogeneity

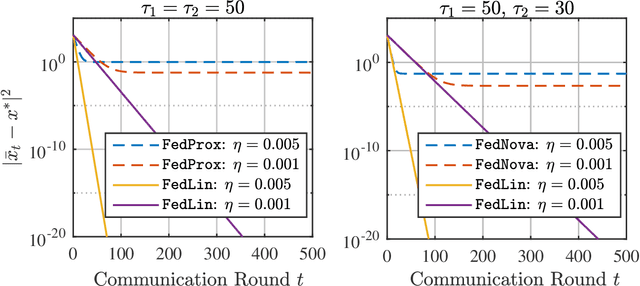
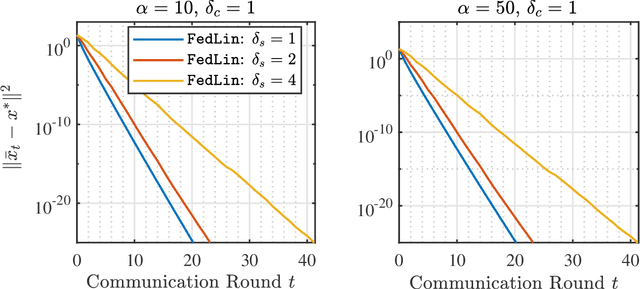
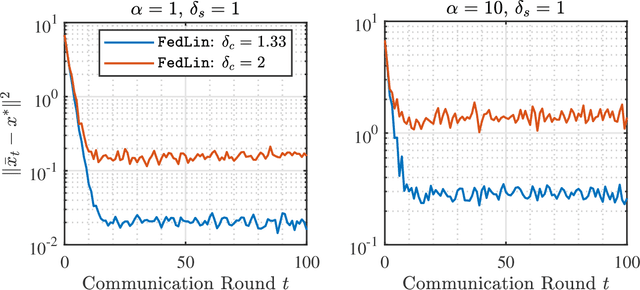
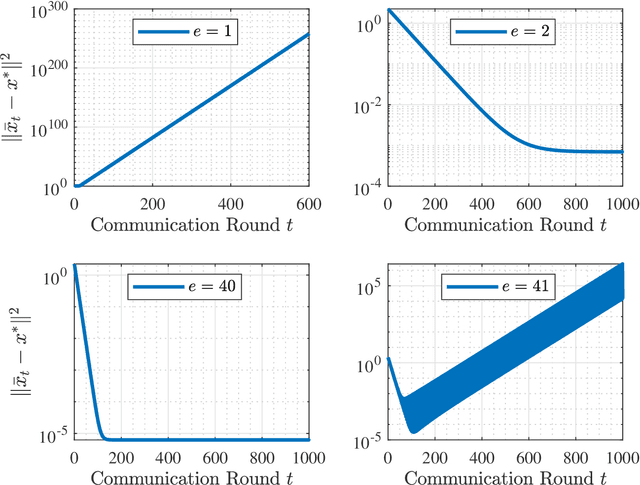
We consider a standard federated learning architecture where a group of clients periodically coordinate with a central server to train a statistical model. We tackle two major challenges in federated learning: (i) objective heterogeneity, which stems from differences in the clients' local loss functions, and (ii) systems heterogeneity, which leads to slow and straggling client devices. Due to such client heterogeneity, we show that existing federated learning algorithms suffer from a fundamental speed-accuracy conflict: they either guarantee linear convergence but to an incorrect point, or convergence to the global minimum but at a sub-linear rate, i.e., fast convergence comes at the expense of accuracy. To address the above limitation, we propose FedLin - a simple, new algorithm that exploits past gradients and employs client-specific learning rates. When the clients' local loss functions are smooth and strongly convex, we show that FedLin guarantees linear convergence to the global minimum. We then establish matching upper and lower bounds on the convergence rate of FedLin that highlight the trade-offs associated with infrequent, periodic communication. Notably, FedLin is the only approach that is able to match centralized convergence rates (up to constants) for smooth strongly convex, convex, and non-convex loss functions despite arbitrary objective and systems heterogeneity. We further show that FedLin preserves linear convergence rates under aggressive gradient sparsification, and quantify the effect of the compression level on the convergence rate.

Non-Monotone Energy-Aware Information Gathering for Heterogeneous Robot Teams

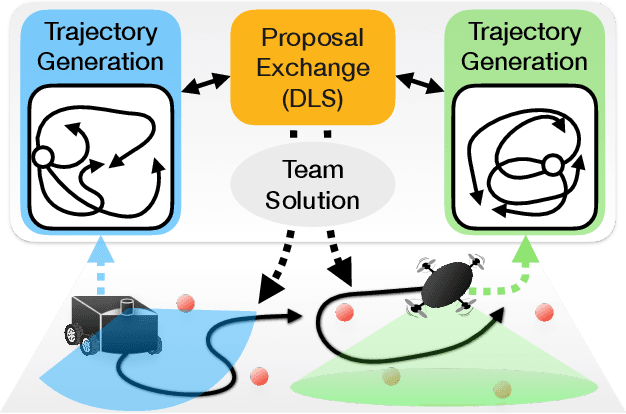
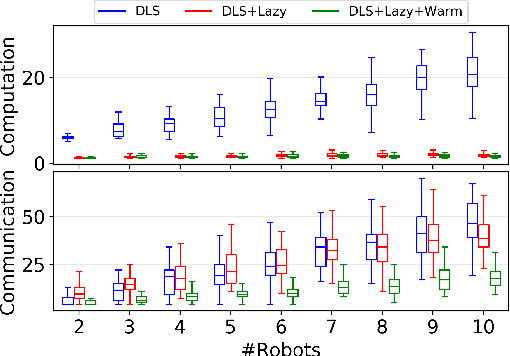
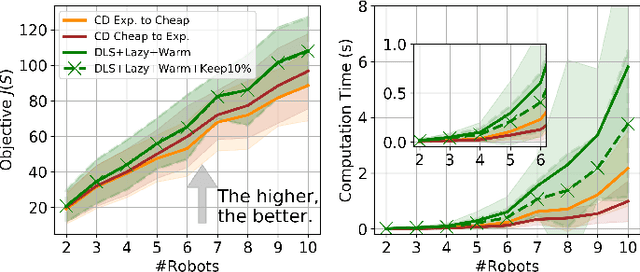
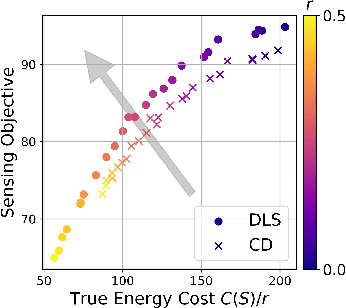
This paper considers the problem of planning trajectories for a team of sensor-equipped robots to reduce uncertainty about a dynamical process. Optimizing the trade-off between information gain and energy cost (e.g., control effort, energy expenditure, distance travelled) is desirable but leads to a non-monotone objective function in the set of robot trajectories. Therefore, common multi-robot planning algorithms based on techniques such as coordinate descent lose their performance guarantees. Methods based on local search provide performance guarantees for optimizing a non-monotone submodular function, but require access to all robots' trajectories, making it not suitable for distributed execution. This work proposes a distributed planning approach based on local search, and shows how to reduce its computation and communication requirements without sacrificing algorithm performance. We demonstrate the efficacy of our proposed method by coordinating robot teams composed of both ground and aerial vehicles with different sensing and control profiles, and evaluate the algorithm's performance in two target tracking scenarios. Our results show up to 60% communication reduction and 80-92% computation reduction on average when coordinating up to 10 robots, while outperforming the coordinate descent based algorithm in achieving a desirable trade-off between sensing and energy expenditure.

Is the brain macroscopically linear? A system identification of resting state dynamics

A central challenge in the computational modeling of neural dynamics is the trade-off between accuracy and simplicity. At the level of individual neurons, nonlinear dynamics are both experimentally established and essential for neuronal functioning. An implicit assumption has thus formed that an accurate computational model of whole-brain dynamics must also be highly nonlinear, whereas linear models may provide a first-order approximation. Here, we provide a rigorous and data-driven investigation of this hypothesis at the level of whole-brain blood-oxygen-level-dependent (BOLD) and macroscopic field potential dynamics by leveraging the theory of system identification. Using functional MRI (fMRI) and intracranial EEG (iEEG), we model the resting state activity of 700 subjects in the Human Connectome Project (HCP) and 122 subjects from the Restoring Active Memory (RAM) project using state-of-the-art linear and nonlinear model families. We assess relative model fit using predictive power, computational complexity, and the extent of residual dynamics unexplained by the model. Contrary to our expectations, linear auto-regressive models achieve the best measures across all three metrics, eliminating the trade-off between accuracy and simplicity. To understand and explain this linearity, we highlight four properties of macroscopic neurodynamics which can counteract or mask microscopic nonlinear dynamics: averaging over space, averaging over time, observation noise, and limited data samples. Whereas the latter two are technological limitations and can improve in the future, the former two are inherent to aggregated macroscopic brain activity. Our results, together with the unparalleled interpretability of linear models, can greatly facilitate our understanding of macroscopic neural dynamics and the principled design of model-based interventions for the treatment of neuropsychiatric disorders.

Sensor-Based Temporal Logic Planning in Uncertain Semantic Maps

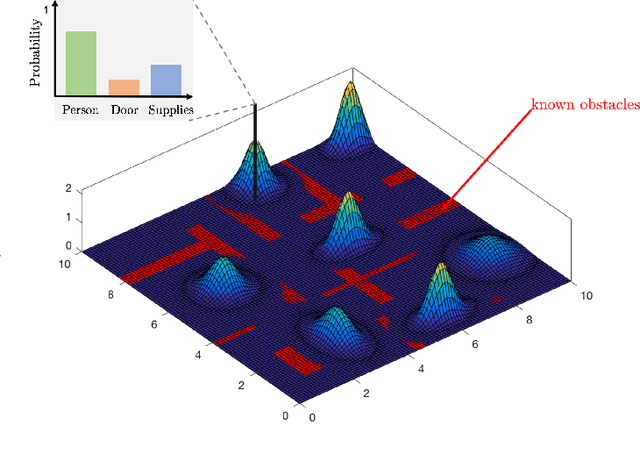
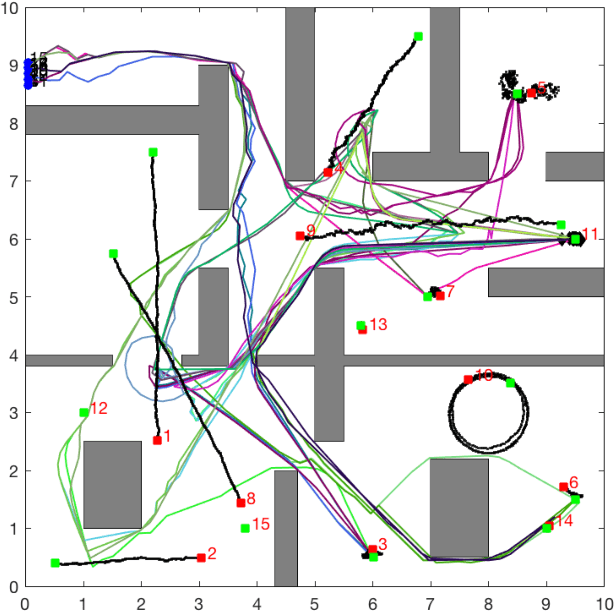
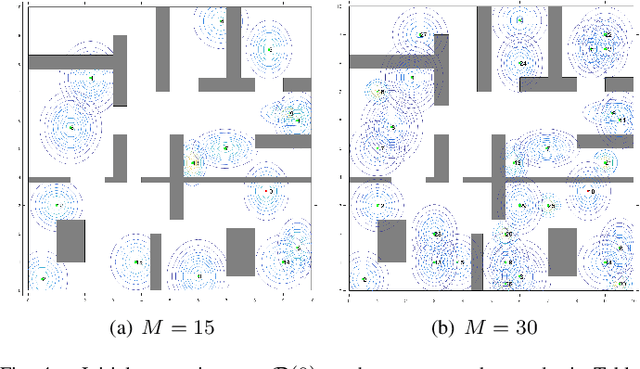
This paper addresses a multi-robot mission planning problem in uncertain semantic environments. The environment is modeled by static labeled landmarks with uncertain positions and classes giving rise to an uncertain semantic map generated by semantic SLAM algorithms. Our goal is to design control policies for sensing robots so that they can accomplish complex collaborative high level tasks captured by global temporal logic specifications. To account for environmental and sensing uncertainty, we extend Linear Temporal Logic (LTL) by including sensor-based predicates allowing us to incorporate uncertainty and probabilistic satisfaction requirements directly into the task specification. The sensor-based LTL planning problem gives rise to an optimal control problem, solved by a novel sampling-based algorithm, that generates open-loop control policies that can be updated online to adapt to the map that is continuously learned by existing semantic SLAM methods. We provide extensive experiments that corroborate the theoretical analysis and show that the proposed algorithm can address large-scale planning tasks in the presence of uncertainty.

Reactive Temporal Logic Planning for Multiple Robots in Unknown Occupancy Grid Maps

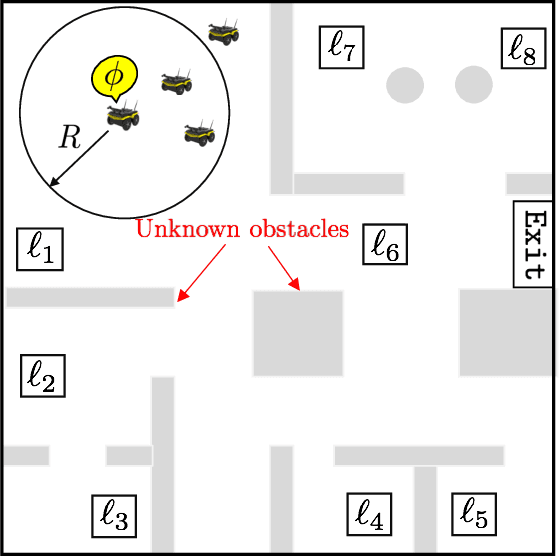
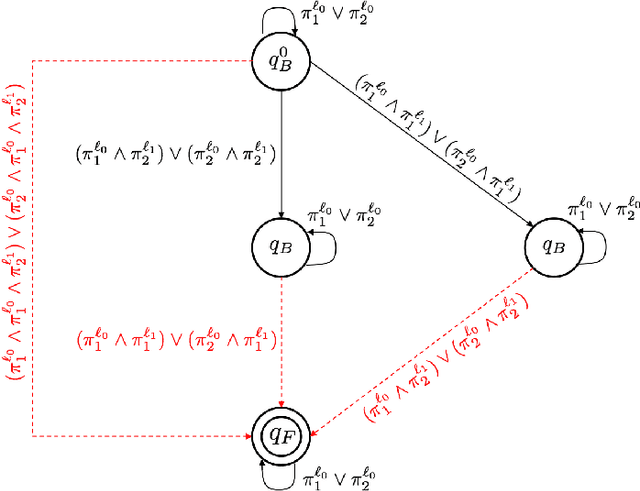
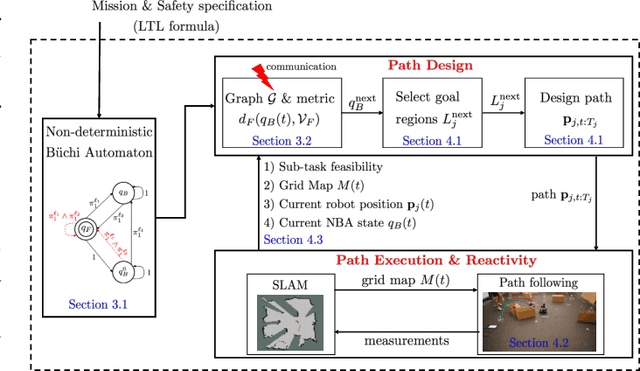
This paper proposes a new reactive temporal logic planning algorithm for multiple robots that operate in environments with unknown geometry modeled using occupancy grid maps. The robots are equipped with individual sensors that allow them to continuously learn a grid map of the unknown environment using existing Simultaneous Localization and Mapping (SLAM) methods. The goal of the robots is to accomplish complex collaborative tasks, captured by global Linear Temporal Logic (LTL) formulas. The majority of existing LTL planning approaches rely on discrete abstractions of the robot dynamics operating in known environments and, as a result, they cannot be applied to the more realistic scenarios where the environment is initially unknown. In this paper, we address this novel challenge by proposing the first reactive, abstraction-free, and distributed LTL planning algorithm that can be applied for complex mission planning of multiple robots operating in unknown environments. The proposed algorithm is reactive, i.e., planning is adapting to the updated environmental map and abstraction-free as it does not rely on designing abstractions of the robot dynamics. Also, our algorithm is distributed in the sense that the global LTL task is decomposed into single-agent reachability problems constructed online based on the continuously learned map. The proposed algorithm is complete under mild assumptions on the structure of the environment and the sensor models. We provide extensive numerical simulations and hardware experiments that illustrate the theoretical analysis and show that the proposed algorithm can address complex planning tasks for large-scale multi-robot systems in unknown environments.

Scalable Reinforcement Learning Policies for Multi-Agent Control

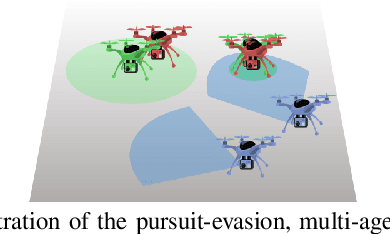
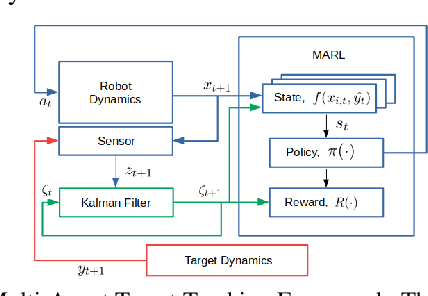
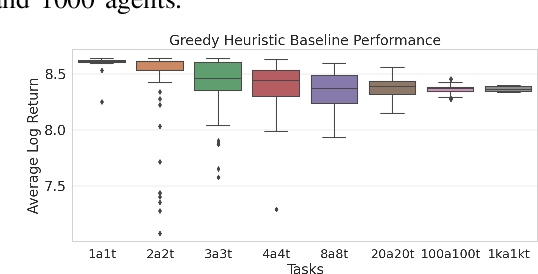
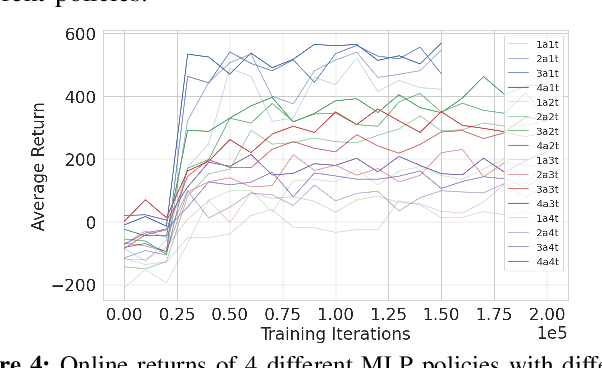
This paper develops a stochastic Multi-Agent Reinforcement Learning (MARL) method to learn control policies that can handle an arbitrary number of external agents; our policies can be executed for tasks consisting of 1000 pursuers and 1000 evaders. We model pursuers as agents with limited on-board sensing and formulate the problem as a decentralized, partially-observable Markov Decision Process. An attention mechanism is used to build a permutation and input-size invariant embedding of the observations for learning a stochastic policy and value function using techniques in entropy-regularized off-policy methods. Simulation experiments on a large number of problems show that our control policies are dramatically scalable and display cooperative behavior in spite of being executed in a decentralized fashion; our methods offer a simple solution to classical multi-agent problems using techniques in reinforcement learning.

Technical Report: Reactive Planning for Mobile Manipulation Tasks in Unexplored Semantic Environments

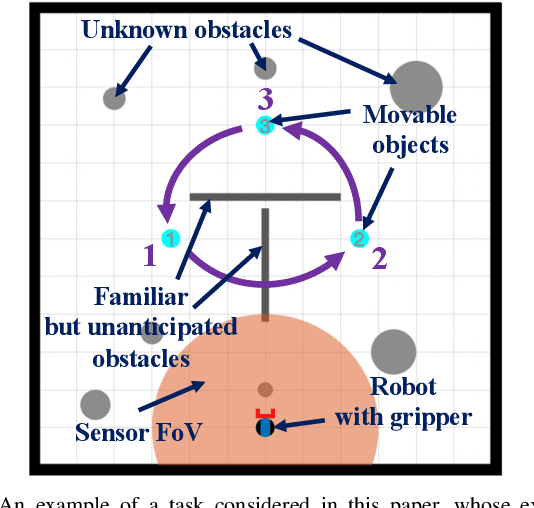
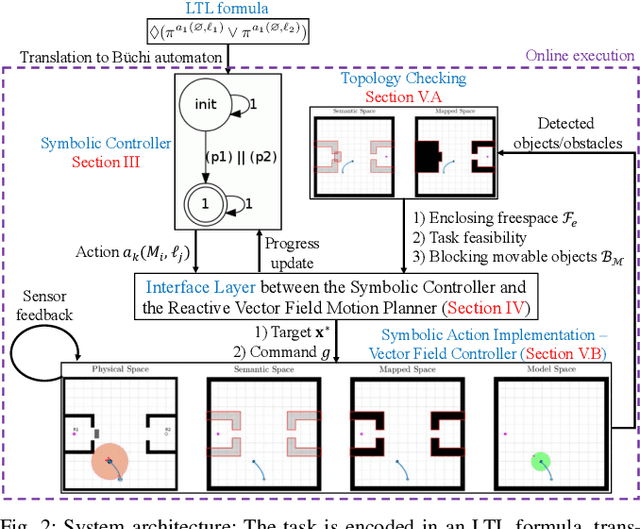
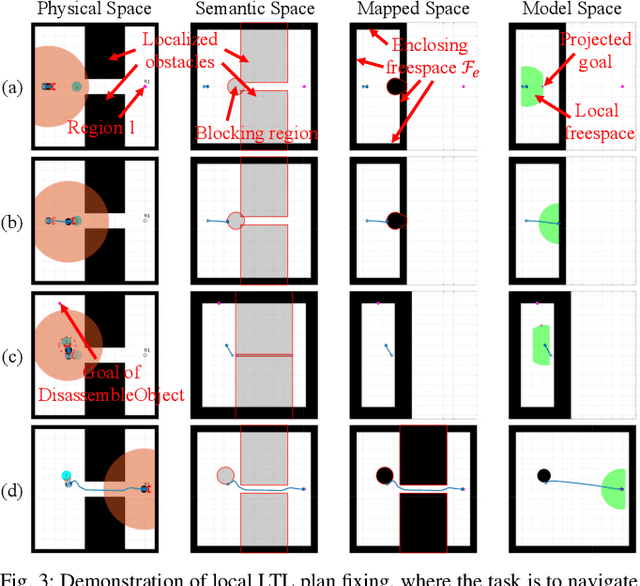
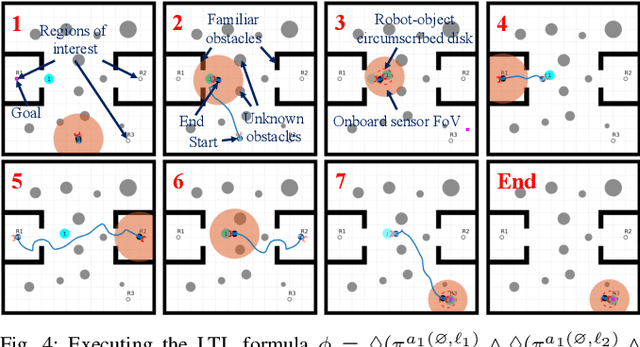
Complex manipulation tasks, such as rearrangement planning of numerous objects, are combinatorially hard problems. Existing algorithms either do not scale well or assume a great deal of prior knowledge about the environment, and few offer any rigorous guarantees. In this paper, we propose a novel hybrid control architecture for achieving such tasks with mobile manipulators. On the discrete side, we enrich a temporal logic specification with mobile manipulation primitives such as moving to a point, and grasping or moving an object. Such specifications are translated to an automaton representation, which orchestrates the physical grounding of the task to mobility or manipulation controllers. The grounding from the discrete to the continuous reactive controller is online and can respond to the discovery of unknown obstacles or decide to push out of the way movable objects that prohibit task accomplishment. Despite the problem complexity, we prove that, under specific conditions, our architecture enjoys provable completeness on the discrete side, provable termination on the continuous side, and avoids all obstacles in the environment. Simulations illustrate the efficiency of our architecture that can handle tasks of increased complexity while also responding to unknown obstacles or unanticipated adverse configurations.

Control Barrier Functions for Unknown Nonlinear Systems using Gaussian Processes

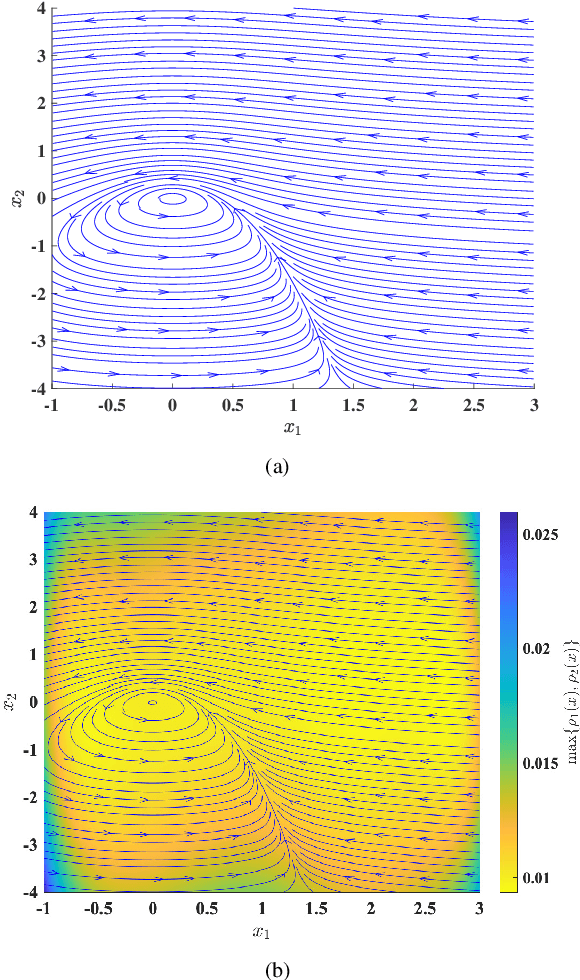
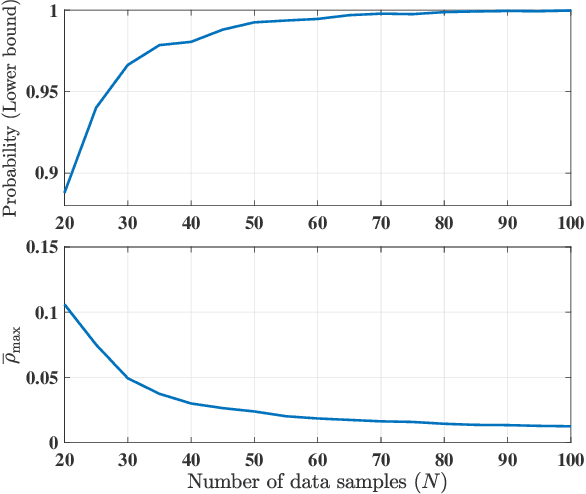
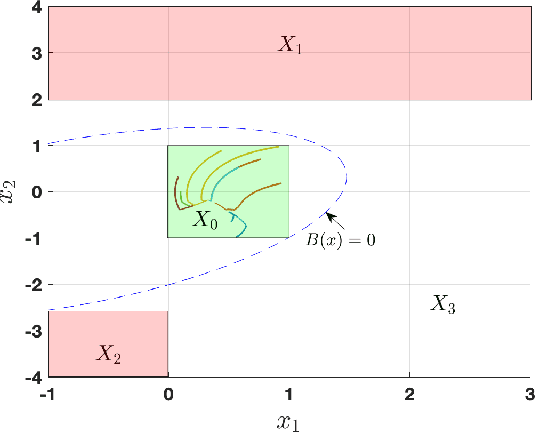
This paper focuses on the controller synthesis for unknown, nonlinear systems while ensuring safety constraints. Our approach consists of two steps, a learning step that uses Gaussian processes and a controller synthesis step that is based on control barrier functions. In the learning step, we use a data-driven approach utilizing Gaussian processes to learn the unknown control affine nonlinear dynamics together with a statistical bound on the accuracy of the learned model. In the second controller synthesis steps, we develop a systematic approach to compute control barrier functions that explicitly take into consideration the uncertainty of the learned model. The control barrier function not only results in a safe controller by construction but also provides a rigorous lower bound on the probability of satisfaction of the safety specification. Finally, we illustrate the effectiveness of the proposed results by synthesizing a safety controller for a jet engine example.