Doubly Stochastic Models: Learning with Unbiased Label Noises and Inference Stability

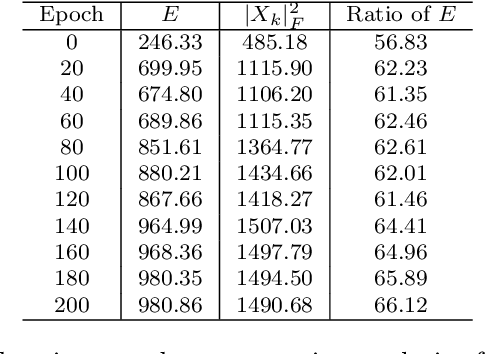
Random label noises (or observational noises) widely exist in practical machine learning settings. While previous studies primarily focus on the affects of label noises to the performance of learning, our work intends to investigate the implicit regularization effects of the label noises, under mini-batch sampling settings of stochastic gradient descent (SGD), with assumptions that label noises are unbiased. Specifically, we analyze the learning dynamics of SGD over the quadratic loss with unbiased label noises, where we model the dynamics of SGD as a stochastic differentiable equation (SDE) with two diffusion terms (namely a Doubly Stochastic Model). While the first diffusion term is caused by mini-batch sampling over the (label-noiseless) loss gradients as many other works on SGD, our model investigates the second noise term of SGD dynamics, which is caused by mini-batch sampling over the label noises, as an implicit regularizer. Our theoretical analysis finds such implicit regularizer would favor some convergence points that could stabilize model outputs against perturbation of parameters (namely inference stability). Though similar phenomenon have been investigated, our work doesn't assume SGD as an Ornstein-Uhlenbeck like process and achieve a more generalizable result with convergence of approximation proved. To validate our analysis, we design two sets of empirical studies to analyze the implicit regularizer of SGD with unbiased random label noises for deep neural networks training and linear regression.

Adversarial Artifact Detection in EEG-Based Brain-Computer Interfaces

Machine learning has achieved great success in electroencephalogram (EEG) based brain-computer interfaces (BCIs). Most existing BCI research focused on improving its accuracy, but few had considered its security. Recent studies, however, have shown that EEG-based BCIs are vulnerable to adversarial attacks, where small perturbations added to the input can cause misclassification. Detection of adversarial examples is crucial to both the understanding of this phenomenon and the defense. This paper, for the first time, explores adversarial detection in EEG-based BCIs. Experiments on two EEG datasets using three convolutional neural networks were performed to verify the performances of multiple detection approaches. We showed that both white-box and black-box attacks can be detected, and the former are easier to detect.

Facial Affect Analysis: Learning from Synthetic Data & Multi-Task Learning Challenges

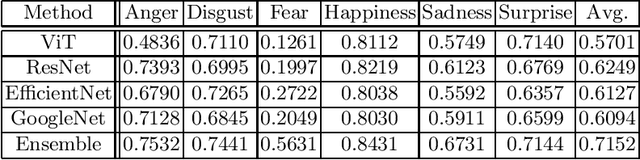
Facial affect analysis remains a challenging task with its setting transitioned from lab-controlled to in-the-wild situations. In this paper, we present novel frameworks to handle the two challenges in the 4th Affective Behavior Analysis In-The-Wild (ABAW) competition: i) Multi-Task-Learning (MTL) Challenge and ii) Learning from Synthetic Data (LSD) Challenge. For MTL challenge, we adopt the SMM-EmotionNet with a better ensemble strategy of feature vectors. For LSD challenge, we propose respective methods to combat the problems of single labels, imbalanced distribution, fine-tuning limitations, and choice of model architectures. Experimental results on the official validation sets from the competition demonstrated that our proposed approaches outperformed baselines by a large margin. The code is available at https://github.com/sylyoung/ABAW4-HUST-ANT.

PyTSK: A Python Toolbox for TSK Fuzzy Systems

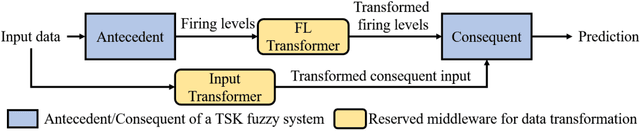
This paper presents PyTSK, a Python toolbox for developing Takagi-Sugeno-Kang (TSK) fuzzy systems. Based on scikit-learn and PyTorch, PyTSK allows users to optimize TSK fuzzy systems using fuzzy clustering or mini-batch gradient descent (MBGD) based algorithms. Several state-of-the-art MBGD-based optimization algorithms are implemented in the toolbox, which can improve the generalization performance of TSK fuzzy systems, especially for big data applications. PyTSK can also be easily extended and customized for more complicated algorithms, such as modifying the structure of TSK fuzzy systems, developing more sophisticated training algorithms, and combining TSK fuzzy systems with neural networks. The code of PyTSK can be found at https://github.com/YuqiCui/pytsk.

AgFlow: Fast Model Selection of Penalized PCA via Implicit Regularization Effects of Gradient Flow

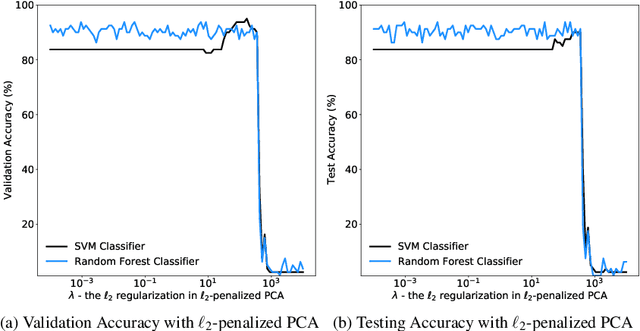
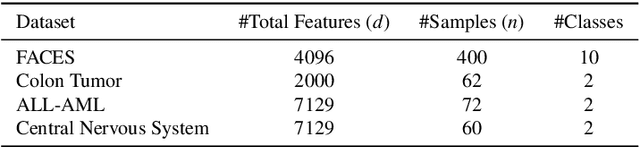
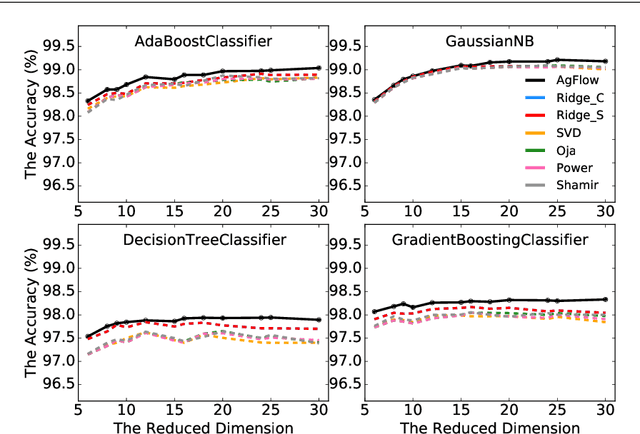
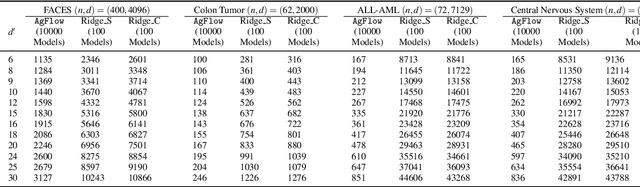
Principal component analysis (PCA) has been widely used as an effective technique for feature extraction and dimension reduction. In the High Dimension Low Sample Size (HDLSS) setting, one may prefer modified principal components, with penalized loadings, and automated penalty selection by implementing model selection among these different models with varying penalties. The earlier work [1, 2] has proposed penalized PCA, indicating the feasibility of model selection in $L_2$- penalized PCA through the solution path of Ridge regression, however, it is extremely time-consuming because of the intensive calculation of matrix inverse. In this paper, we propose a fast model selection method for penalized PCA, named Approximated Gradient Flow (AgFlow), which lowers the computation complexity through incorporating the implicit regularization effect introduced by (stochastic) gradient flow [3, 4] and obtains the complete solution path of $L_2$-penalized PCA under varying $L_2$-regularization. We perform extensive experiments on real-world datasets. AgFlow outperforms existing methods (Oja [5], Power [6], and Shamir [7] and the vanilla Ridge estimators) in terms of computation costs.

Exploring the Common Principal Subspace of Deep Features in Neural Networks

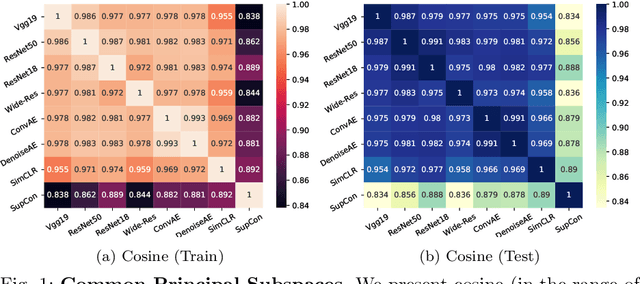
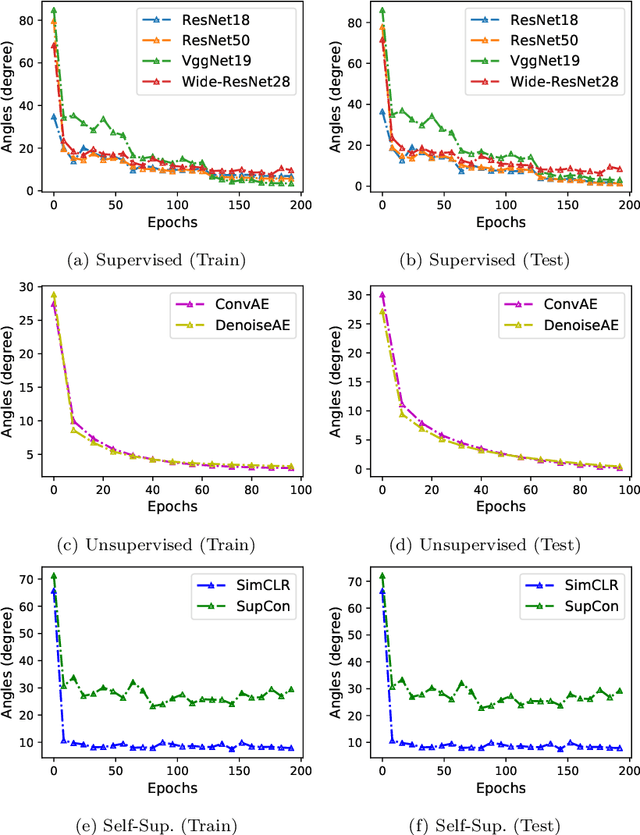
We find that different Deep Neural Networks (DNNs) trained with the same dataset share a common principal subspace in latent spaces, no matter in which architectures (e.g., Convolutional Neural Networks (CNNs), Multi-Layer Preceptors (MLPs) and Autoencoders (AEs)) the DNNs were built or even whether labels have been used in training (e.g., supervised, unsupervised, and self-supervised learning). Specifically, we design a new metric $\mathcal{P}$-vector to represent the principal subspace of deep features learned in a DNN, and propose to measure angles between the principal subspaces using $\mathcal{P}$-vectors. Small angles (with cosine close to $1.0$) have been found in the comparisons between any two DNNs trained with different algorithms/architectures. Furthermore, during the training procedure from random scratch, the angle decrease from a larger one ($70^\circ-80^\circ$ usually) to the small one, which coincides the progress of feature space learning from scratch to convergence. Then, we carry out case studies to measure the angle between the $\mathcal{P}$-vector and the principal subspace of training dataset, and connect such angle with generalization performance. Extensive experiments with practically-used Multi-Layer Perceptron (MLPs), AEs and CNNs for classification, image reconstruction, and self-supervised learning tasks on MNIST, CIFAR-10 and CIFAR-100 datasets have been done to support our claims with solid evidences. Interpretability of Deep Learning, Feature Learning, and Subspaces of Deep Features

Optimization Variance: Exploring Generalization Properties of DNNs

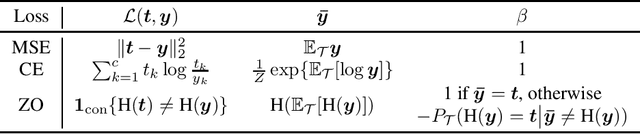
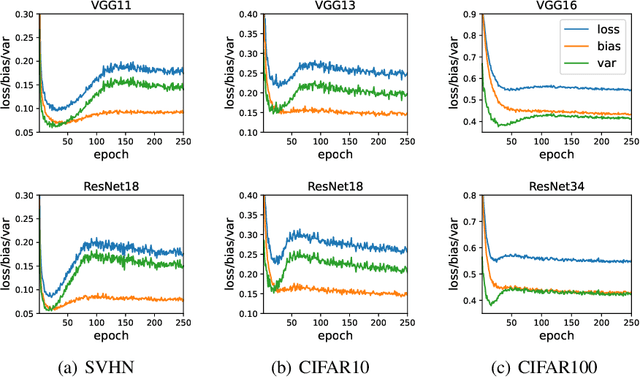
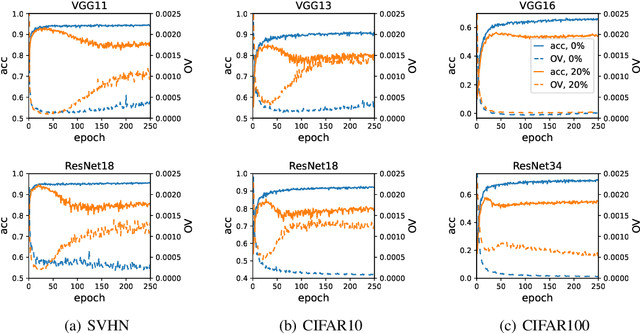
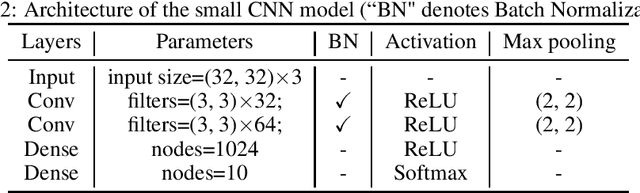
Unlike the conventional wisdom in statistical learning theory, the test error of a deep neural network (DNN) often demonstrates double descent: as the model complexity increases, it first follows a classical U-shaped curve and then shows a second descent. Through bias-variance decomposition, recent studies revealed that the bell-shaped variance is the major cause of model-wise double descent (when the DNN is widened gradually). This paper investigates epoch-wise double descent, i.e., the test error of a DNN also shows double descent as the number of training epoches increases. By extending the bias-variance analysis to epoch-wise double descent of the zero-one loss, we surprisingly find that the variance itself, without the bias, varies consistently with the test error. Inspired by this result, we propose a novel metric, optimization variance (OV), to measure the diversity of model updates caused by the stochastic gradients of random training batches drawn in the same iteration. OV can be estimated using samples from the training set only but correlates well with the (unknown) \emph{test} error, and hence early stopping may be achieved without using a validation set.

Adversarial Attacks and Defenses in Physiological Computing: A Systematic Review

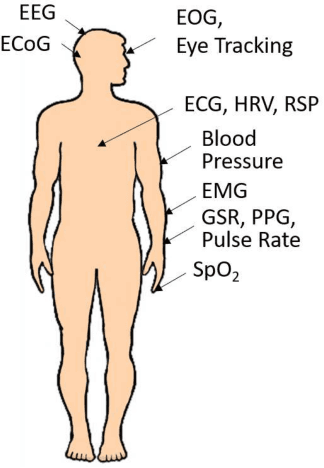
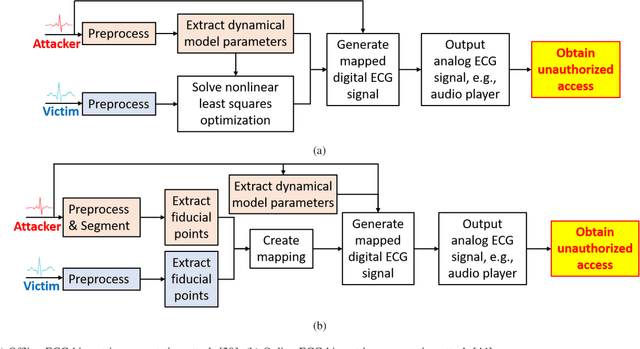
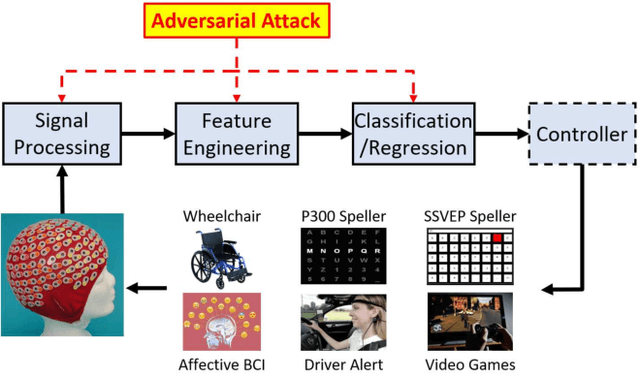
Physiological computing uses human physiological data as system inputs in real time. It includes, or significantly overlaps with, brain-computer interfaces, affective computing, adaptive automation, health informatics, and physiological signal based biometrics. Physiological computing increases the communication bandwidth from the user to the computer, but is also subject to various types of adversarial attacks, in which the attacker deliberately manipulates the training and/or test examples to hijack the machine learning algorithm output, leading to possibly user confusion, frustration, injury, or even death. However, the vulnerability of physiological computing systems has not been paid enough attention to, and there does not exist a comprehensive review on adversarial attacks to it. This paper fills this gap, by providing a systematic review on the main research areas of physiological computing, different types of adversarial attacks and their applications to physiological computing, and the corresponding defense strategies. We hope this review will attract more research interests on the vulnerability of physiological computing systems, and more importantly, defense strategies to make them more secure.

Curse of Dimensionality for TSK Fuzzy Neural Networks: Explanation and Solutions

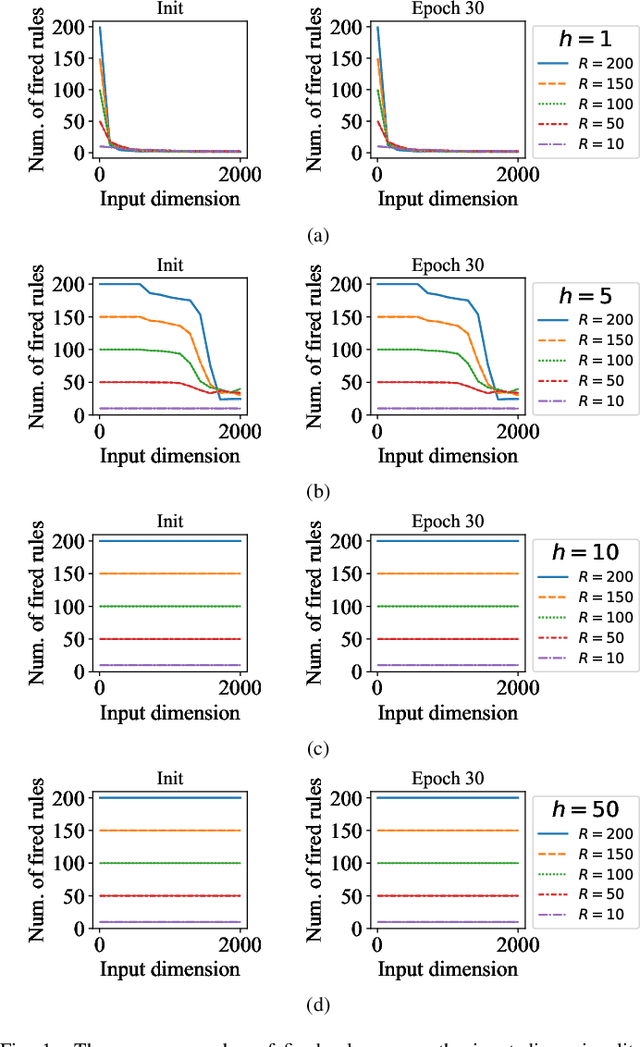
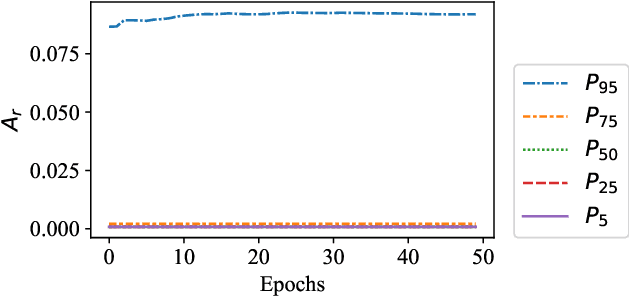
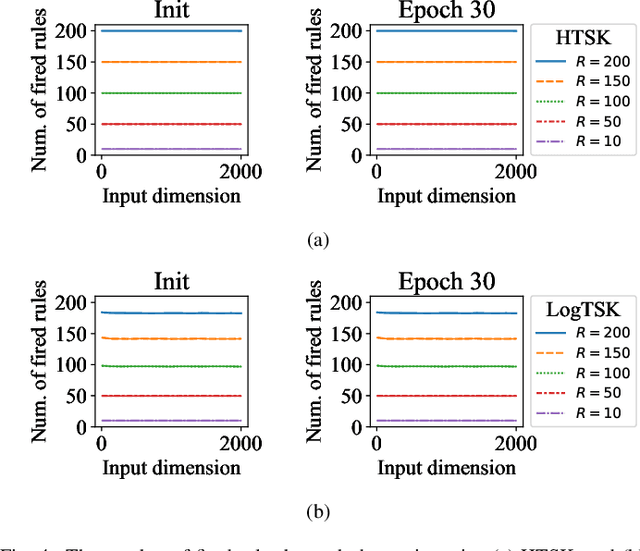
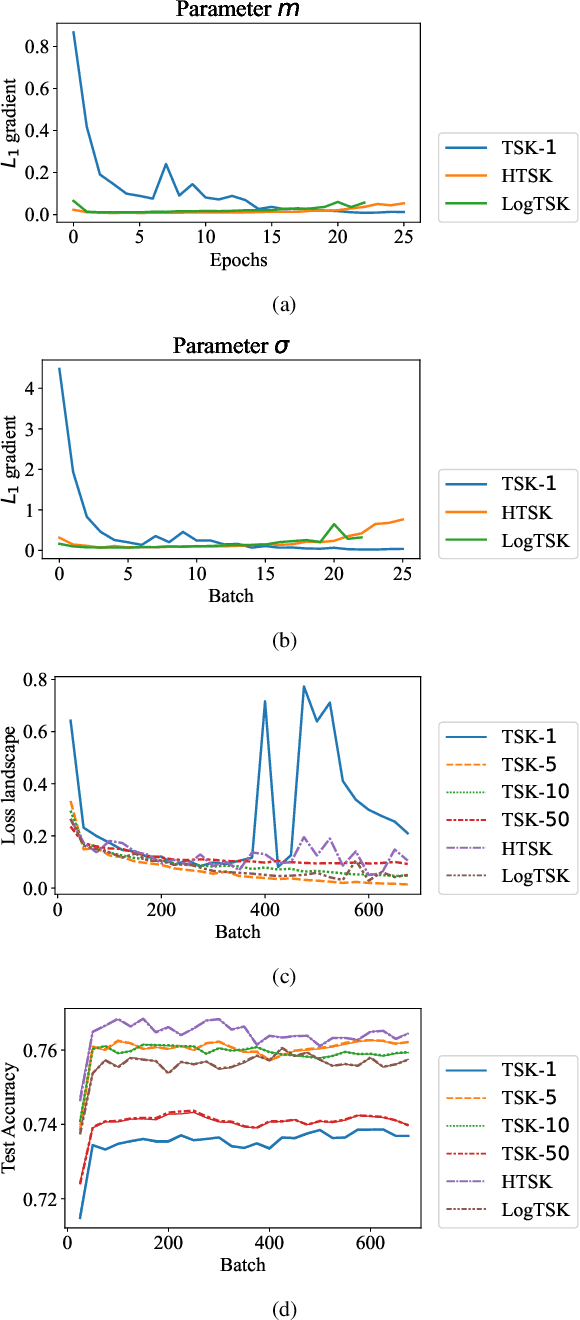
Takagi-Sugeno-Kang (TSK) fuzzy system with Gaussian membership functions (MFs) is one of the most widely used fuzzy systems in machine learning. However, it usually has difficulty handling high-dimensional datasets. This paper explores why TSK fuzzy systems with Gaussian MFs may fail on high-dimensional inputs. After transforming defuzzification to an equivalent form of softmax function, we find that the poor performance is due to the saturation of softmax. We show that two defuzzification operations, LogTSK and HTSK, the latter of which is first proposed in this paper, can avoid the saturation. Experimental results on datasets with various dimensionalities validated our analysis and demonstrated the effectiveness of LogTSK and HTSK.

FCM-RDpA: TSK Fuzzy Regression Model Construction Using Fuzzy C-Means Clustering, Regularization, DropRule, and Powerball AdaBelief

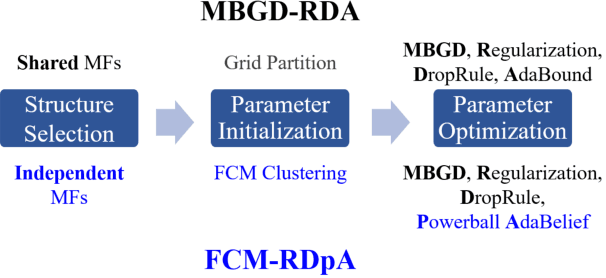
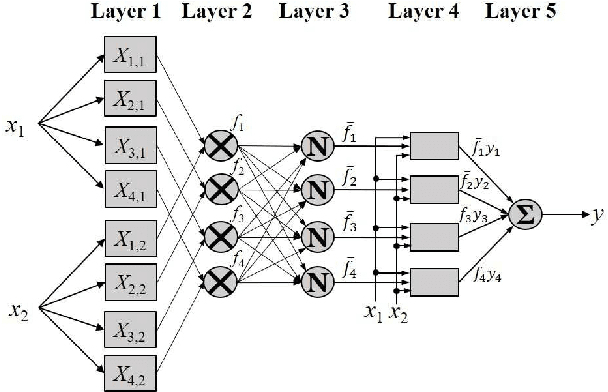
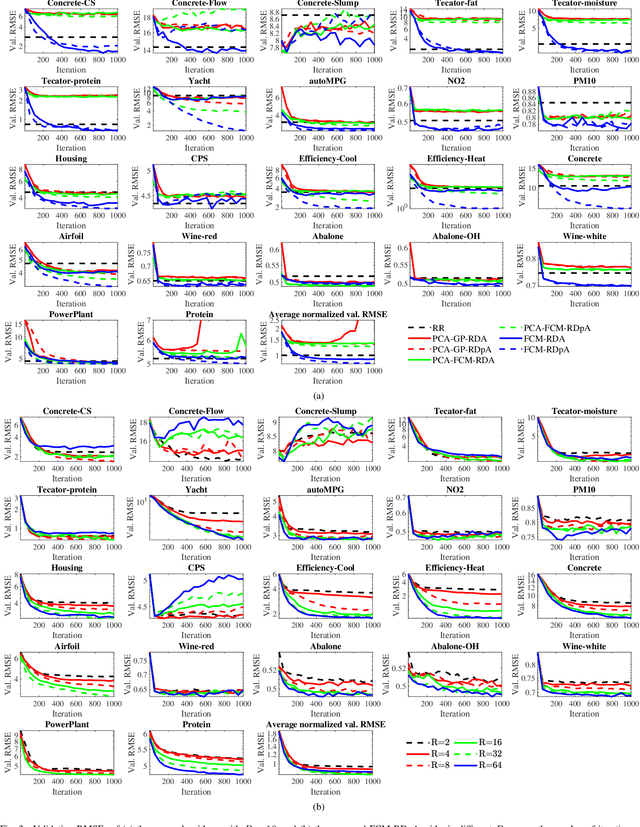
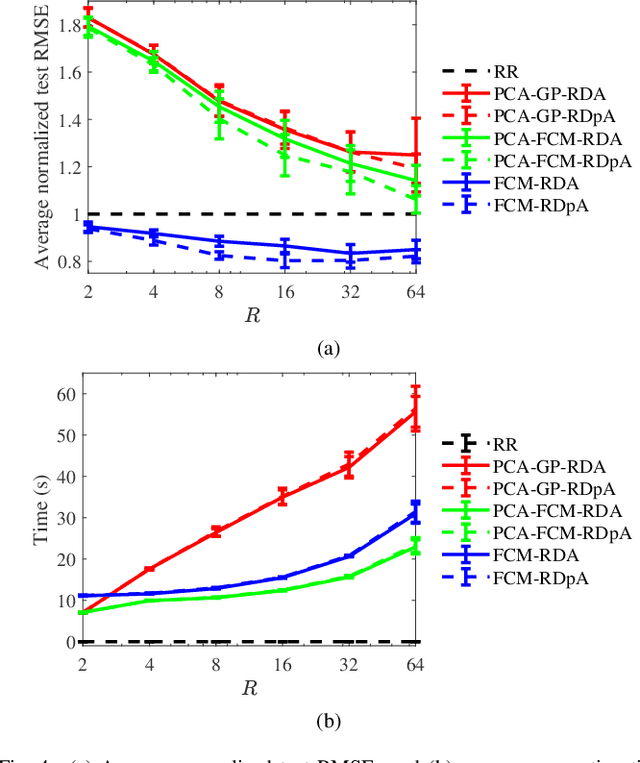
To effectively optimize Takagi-Sugeno-Kang (TSK) fuzzy systems for regression problems, a mini-batch gradient descent with regularization, DropRule, and AdaBound (MBGD-RDA) algorithm was recently proposed. This paper further proposes FCM-RDpA, which improves MBGD-RDA by replacing the grid partition approach in rule initialization by fuzzy c-means clustering, and AdaBound by Powerball AdaBelief, which integrates recently proposed Powerball gradient and AdaBelief to further expedite and stabilize parameter optimization. Extensive experiments on 22 regression datasets with various sizes and dimensionalities validated the superiority of FCM-RDpA over MBGD-RDA, especially when the feature dimensionality is higher. We also propose an additional approach, FCM-RDpAx, that further improves FCM-RDpA by using augmented features in both the antecedents and consequents of the rules.