Machine Learning for Mechanical Ventilation Control

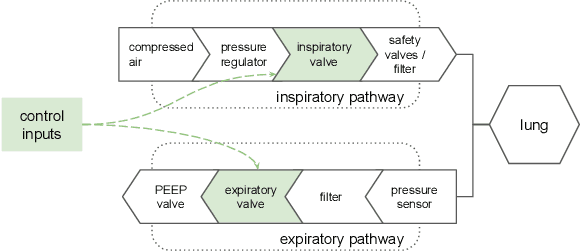
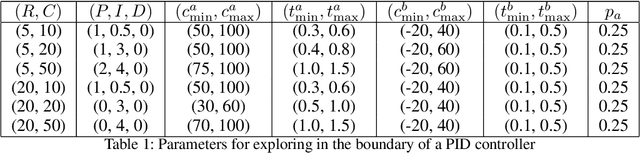
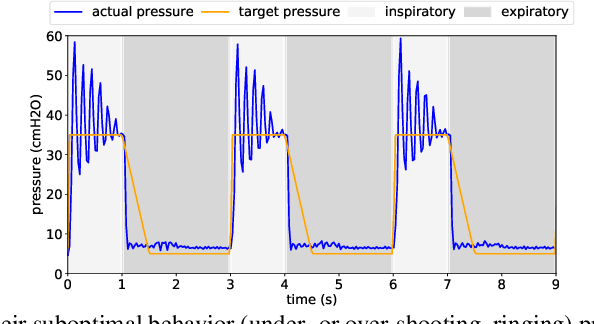
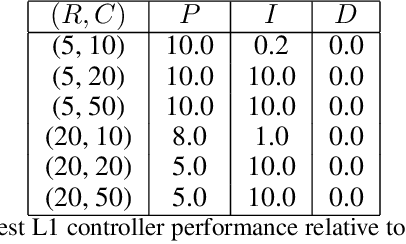
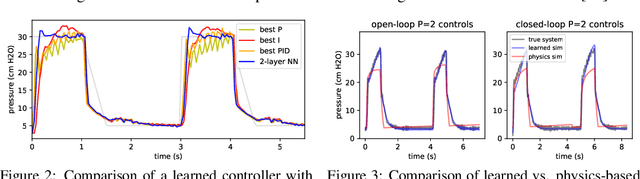
We consider the problem of controlling an invasive mechanical ventilator for pressure-controlled ventilation: a controller must let air in and out of a sedated patient's lungs according to a trajectory of airway pressures specified by a clinician. Hand-tuned PID controllers and similar variants have comprised the industry standard for decades, yet can behave poorly by over- or under-shooting their target or oscillating rapidly. We consider a data-driven machine learning approach: First, we train a simulator based on data we collect from an artificial lung. Then, we train deep neural network controllers on these simulators.We show that our controllers are able to track target pressure waveforms significantly better than PID controllers. We further show that a learned controller generalizes across lungs with varying characteristics much more readily than PID controllers do.

Deluca -- A Differentiable Control Library: Environments, Methods, and Benchmarking

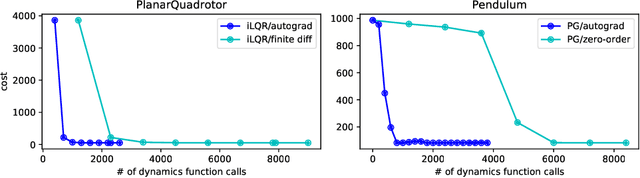
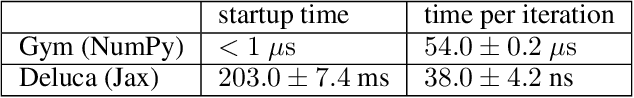
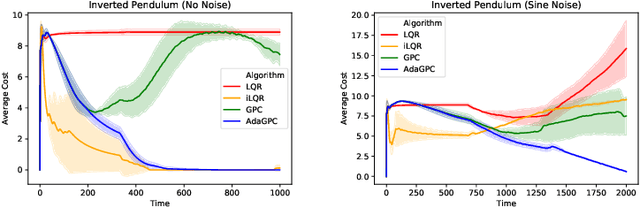
We present an open-source library of natively differentiable physics and robotics environments, accompanied by gradient-based control methods and a benchmark-ing suite. The introduced environments allow auto-differentiation through the simulation dynamics, and thereby permit fast training of controllers. The library features several popular environments, including classical control settings from OpenAI Gym. We also provide a novel differentiable environment, based on deep neural networks, that simulates medical ventilation. We give several use-cases of new scientific results obtained using the library. This includes a medical ventilator simulator and controller, an adaptive control method for time-varying linear dynamical systems, and new gradient-based methods for control of linear dynamical systems with adversarial perturbations.

Stochastic Optimization with Laggard Data Pipelines

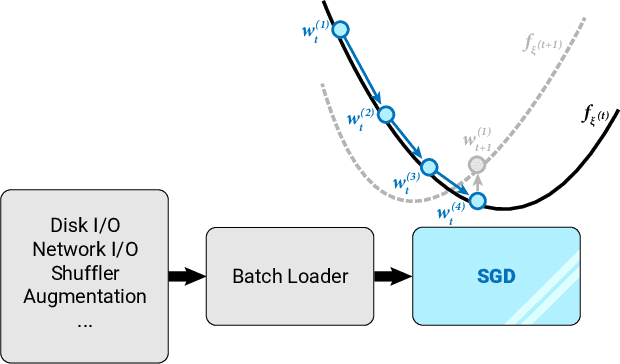
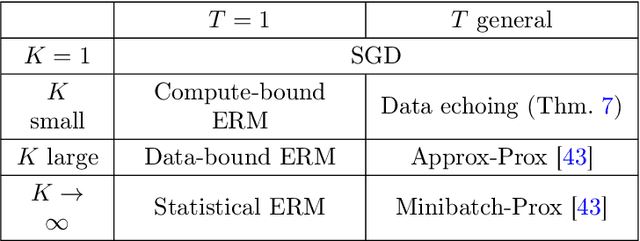
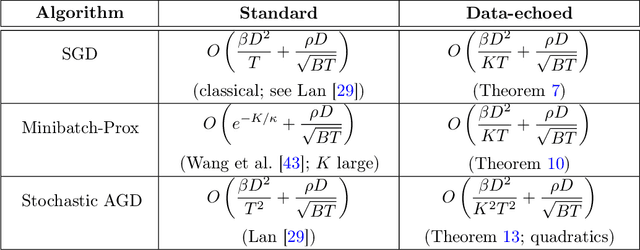
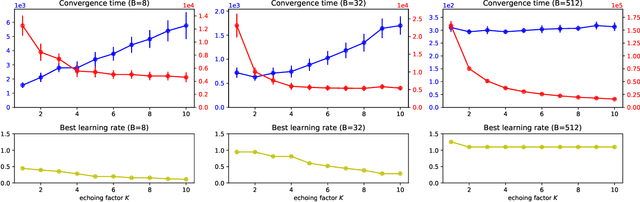
State-of-the-art optimization is steadily shifting towards massively parallel pipelines with extremely large batch sizes. As a consequence, CPU-bound preprocessing and disk/memory/network operations have emerged as new performance bottlenecks, as opposed to hardware-accelerated gradient computations. In this regime, a recently proposed approach is data echoing (Choi et al., 2019), which takes repeated gradient steps on the same batch while waiting for fresh data to arrive from upstream. We provide the first convergence analyses of "data-echoed" extensions of common optimization methods, showing that they exhibit provable improvements over their synchronous counterparts. Specifically, we show that in convex optimization with stochastic minibatches, data echoing affords speedups on the curvature-dominated part of the convergence rate, while maintaining the optimal statistical rate.

Disentangling Adaptive Gradient Methods from Learning Rates

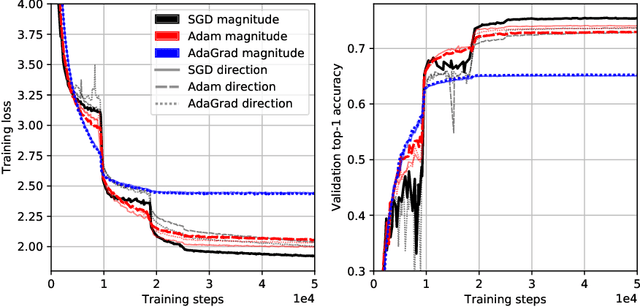
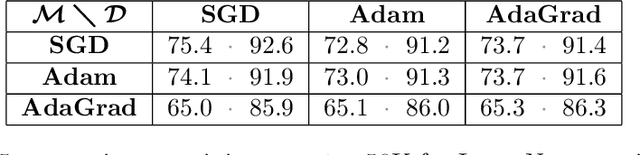
We investigate several confounding factors in the evaluation of optimization algorithms for deep learning. Primarily, we take a deeper look at how adaptive gradient methods interact with the learning rate schedule, a notoriously difficult-to-tune hyperparameter which has dramatic effects on the convergence and generalization of neural network training. We introduce a "grafting" experiment which decouples an update's magnitude from its direction, finding that many existing beliefs in the literature may have arisen from insufficient isolation of the implicit schedule of step sizes. Alongside this contribution, we present some empirical and theoretical retrospectives on the generalization of adaptive gradient methods, aimed at bringing more clarity to this space.

No-Regret Prediction in Marginally Stable Systems

We consider the problem of online prediction in a marginally stable linear dynamical system subject to bounded adversarial or (non-isotropic) stochastic perturbations. This poses two challenges. Firstly, the system is in general unidentifiable, so recent and classical results on parameter recovery do not apply. Secondly, because we allow the system to be marginally stable, the state can grow polynomially with time; this causes standard regret bounds in online convex optimization to be vacuous. In spite of these challenges, we show that the online least-squares algorithm achieves sublinear regret (improvable to polylogarithmic in the stochastic setting), with polynomial dependence on the system's parameters. This requires a refined regret analysis, including a structural lemma showing the current state of the system to be a small linear combination of past states, even if the state grows polynomially. By applying our techniques to learning an autoregressive filter, we also achieve logarithmic regret in the partially observed setting under Gaussian noise, with polynomial dependence on the memory of the associated Kalman filter.

Calibration, Entropy Rates, and Memory in Language Models

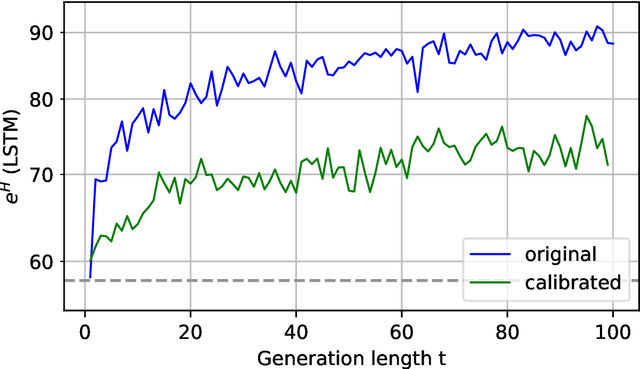
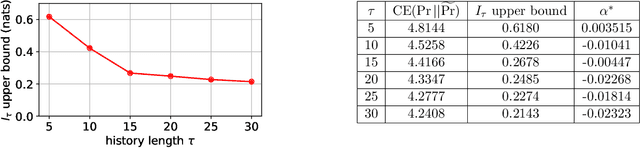
Building accurate language models that capture meaningful long-term dependencies is a core challenge in natural language processing. Towards this end, we present a calibration-based approach to measure long-term discrepancies between a generative sequence model and the true distribution, and use these discrepancies to improve the model. Empirically, we show that state-of-the-art language models, including LSTMs and Transformers, are \emph{miscalibrated}: the entropy rates of their generations drift dramatically upward over time. We then provide provable methods to mitigate this phenomenon. Furthermore, we show how this calibration-based approach can also be used to measure the amount of memory that language models use for prediction.

Robust guarantees for learning an autoregressive filter

The optimal predictor for a linear dynamical system (with hidden state and Gaussian noise) takes the form of an autoregressive linear filter, namely the Kalman filter. However, a fundamental problem in reinforcement learning and control theory is to make optimal predictions in an unknown dynamical system. To this end, we take the approach of directly learning an autoregressive filter for time-series prediction under unknown dynamics. Our analysis differs from previous statistical analyses in that we regress not only on the inputs to the dynamical system, but also the outputs, which is essential to dealing with process noise. The main challenge is to estimate the filter under worst case input (in $\mathcal H_\infty$ norm), for which we use an $L^\infty$-based objective rather than ordinary least-squares. For learning an autoregressive model, our algorithm has optimal sample complexity in terms of the rollout length, which does not seem to be attained by naive least-squares.

Extreme Tensoring for Low-Memory Preconditioning

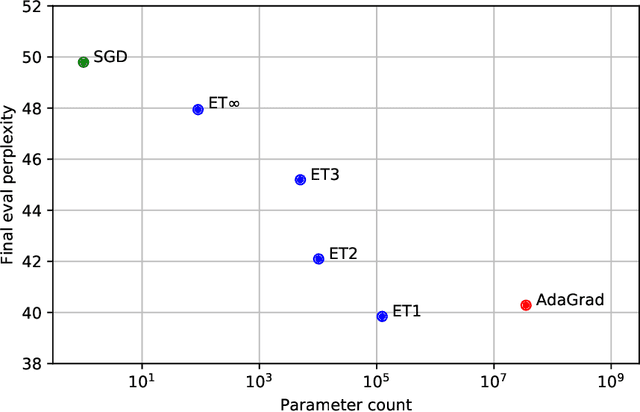
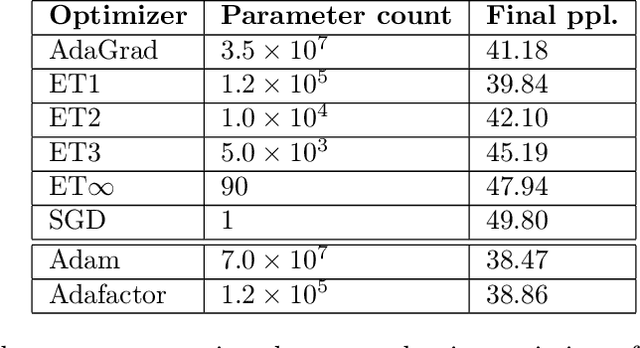
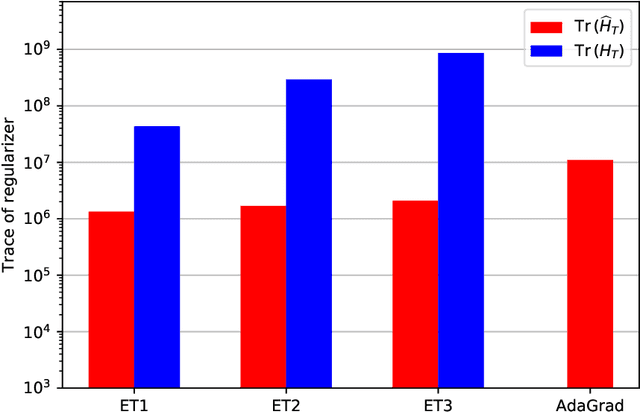
State-of-the-art models are now trained with billions of parameters, reaching hardware limits in terms of memory consumption. This has created a recent demand for memory-efficient optimizers. To this end, we investigate the limits and performance tradeoffs of memory-efficient adaptively preconditioned gradient methods. We propose extreme tensoring for high-dimensional stochastic optimization, showing that an optimizer needs very little memory to benefit from adaptive preconditioning. Our technique applies to arbitrary models (not necessarily with tensor-shaped parameters), and is accompanied by regret and convergence guarantees, which shed light on the tradeoffs between preconditioner quality and expressivity. On a large-scale NLP model, we reduce the optimizer memory overhead by three orders of magnitude, without degrading performance.

The Case for Full-Matrix Adaptive Regularization

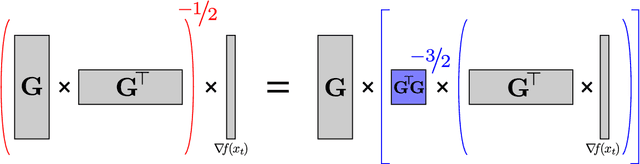
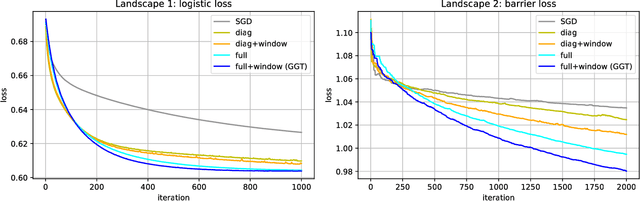
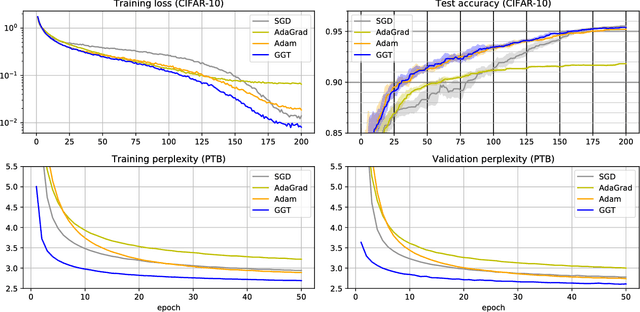
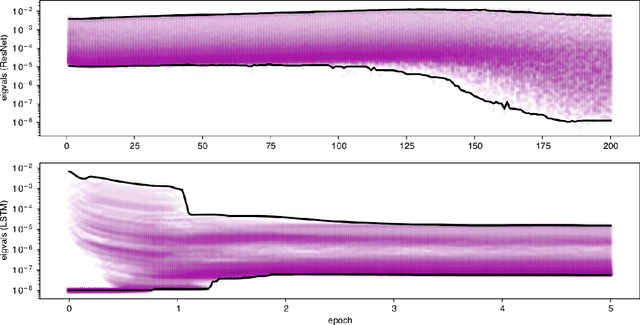
Adaptive regularization methods come in diagonal and full-matrix variants. However, only the former have enjoyed widespread adoption in training large-scale deep models. This is due to the computational overhead of manipulating a full matrix in high dimension. In this paper, we show how to make full-matrix adaptive regularization practical and useful. We present GGT, a truly scalable full-matrix adaptive optimizer. At the heart of our algorithm is an efficient method for computing the inverse square root of a low-rank matrix. We show that GGT converges to first-order local minima, providing the first rigorous theoretical analysis of adaptive regularization in non-convex optimization. In preliminary experiments, GGT trains faster across a variety of synthetic tasks and standard deep learning benchmarks.

Not-So-Random Features

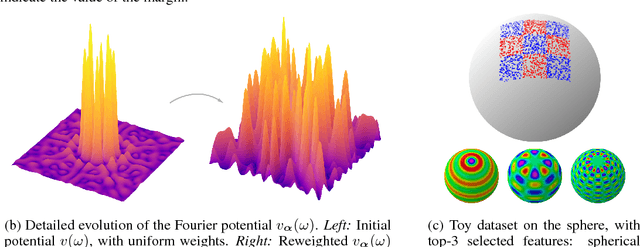
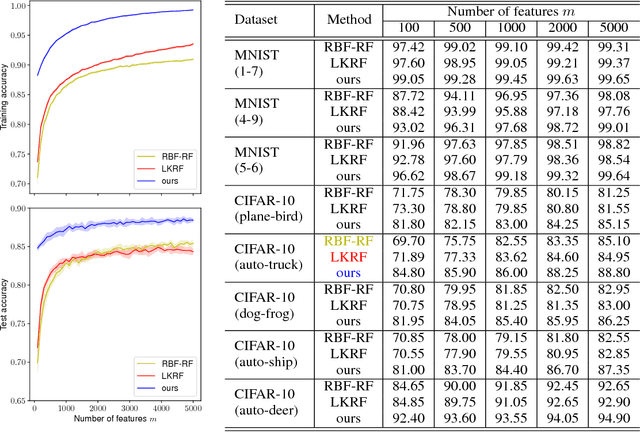
We propose a principled method for kernel learning, which relies on a Fourier-analytic characterization of translation-invariant or rotation-invariant kernels. Our method produces a sequence of feature maps, iteratively refining the SVM margin. We provide rigorous guarantees for optimality and generalization, interpreting our algorithm as online equilibrium-finding dynamics in a certain two-player min-max game. Evaluations on synthetic and real-world datasets demonstrate scalability and consistent improvements over related random features-based methods.