sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

All-in-one simulation-based inference

Amortized Bayesian inference trains neural networks to solve stochastic inference problems using model simulations, thereby making it possible to rapidly perform Bayesian inference for any newly observed data. However, current simulation-based amortized inference methods are simulation-hungry and inflexible: They require the specification of a fixed parametric prior, simulator, and inference tasks ahead of time. Here, we present a new amortized inference method -- the Simformer -- which overcomes these limitations. By training a probabilistic diffusion model with transformer architectures, the Simformer outperforms current state-of-the-art amortized inference approaches on benchmark tasks and is substantially more flexible: It can be applied to models with function-valued parameters, it can handle inference scenarios with missing or unstructured data, and it can sample arbitrary conditionals of the joint distribution of parameters and data, including both posterior and likelihood. We showcase the performance and flexibility of the Simformer on simulators from ecology, epidemiology, and neuroscience, and demonstrate that it opens up new possibilities and application domains for amortized Bayesian inference on simulation-based models.

A Practical Guide to Statistical Distances for Evaluating Generative Models in Science

Generative models are invaluable in many fields of science because of their ability to capture high-dimensional and complicated distributions, such as photo-realistic images, protein structures, and connectomes. How do we evaluate the samples these models generate? This work aims to provide an accessible entry point to understanding popular notions of statistical distances, requiring only foundational knowledge in mathematics and statistics. We focus on four commonly used notions of statistical distances representing different methodologies: Using low-dimensional projections (Sliced-Wasserstein; SW), obtaining a distance using classifiers (Classifier Two-Sample Tests; C2ST), using embeddings through kernels (Maximum Mean Discrepancy; MMD), or neural networks (Fr\'echet Inception Distance; FID). We highlight the intuition behind each distance and explain their merits, scalability, complexity, and pitfalls. To demonstrate how these distances are used in practice, we evaluate generative models from different scientific domains, namely a model of decision making and a model generating medical images. We showcase that distinct distances can give different results on similar data. Through this guide, we aim to help researchers to use, interpret, and evaluate statistical distances for generative models in science.

Diffusion Tempering Improves Parameter Estimation with Probabilistic Integrators for Ordinary Differential Equations

Ordinary differential equations (ODEs) are widely used to describe dynamical systems in science, but identifying parameters that explain experimental measurements is challenging. In particular, although ODEs are differentiable and would allow for gradient-based parameter optimization, the nonlinear dynamics of ODEs often lead to many local minima and extreme sensitivity to initial conditions. We therefore propose diffusion tempering, a novel regularization technique for probabilistic numerical methods which improves convergence of gradient-based parameter optimization in ODEs. By iteratively reducing a noise parameter of the probabilistic integrator, the proposed method converges more reliably to the true parameters. We demonstrate that our method is effective for dynamical systems of different complexity and show that it obtains reliable parameter estimates for a Hodgkin-Huxley model with a practically relevant number of parameters.

Amortized Bayesian Decision Making for simulation-based models

Simulation-based inference (SBI) provides a powerful framework for inferring posterior distributions of stochastic simulators in a wide range of domains. In many settings, however, the posterior distribution is not the end goal itself -- rather, the derived parameter values and their uncertainties are used as a basis for deciding what actions to take. Unfortunately, because posterior distributions provided by SBI are (potentially crude) approximations of the true posterior, the resulting decisions can be suboptimal. Here, we address the question of how to perform Bayesian decision making on stochastic simulators, and how one can circumvent the need to compute an explicit approximation to the posterior. Our method trains a neural network on simulated data and can predict the expected cost given any data and action, and can, thus, be directly used to infer the action with lowest cost. We apply our method to several benchmark problems and demonstrate that it induces similar cost as the true posterior distribution. We then apply the method to infer optimal actions in a real-world simulator in the medical neurosciences, the Bayesian Virtual Epileptic Patient, and demonstrate that it allows to infer actions associated with low cost after few simulations.

Generalized Bayesian Inference for Scientific Simulators via Amortized Cost Estimation

Simulation-based inference (SBI) enables amortized Bayesian inference for simulators with implicit likelihoods. But when we are primarily interested in the quality of predictive simulations, or when the model cannot exactly reproduce the observed data (i.e., is misspecified), targeting the Bayesian posterior may be overly restrictive. Generalized Bayesian Inference (GBI) aims to robustify inference for (misspecified) simulator models, replacing the likelihood-function with a cost function that evaluates the goodness of parameters relative to data. However, GBI methods generally require running multiple simulations to estimate the cost function at each parameter value during inference, making the approach computationally infeasible for even moderately complex simulators. Here, we propose amortized cost estimation (ACE) for GBI to address this challenge: We train a neural network to approximate the cost function, which we define as the expected distance between simulations produced by a parameter and observed data. The trained network can then be used with MCMC to infer GBI posteriors for any observation without running additional simulations. We show that, on several benchmark tasks, ACE accurately predicts cost and provides predictive simulations that are closer to synthetic observations than other SBI methods, especially for misspecified simulators. Finally, we apply ACE to infer parameters of the Hodgkin-Huxley model given real intracellular recordings from the Allen Cell Types Database. ACE identifies better data-matching parameters while being an order of magnitude more simulation-efficient than a standard SBI method. In summary, ACE combines the strengths of SBI methods and GBI to perform robust and simulation-amortized inference for scientific simulators.

Adversarial robustness of amortized Bayesian inference

Bayesian inference usually requires running potentially costly inference procedures separately for every new observation. In contrast, the idea of amortized Bayesian inference is to initially invest computational cost in training an inference network on simulated data, which can subsequently be used to rapidly perform inference (i.e., to return estimates of posterior distributions) for new observations. This approach has been applied to many real-world models in the sciences and engineering, but it is unclear how robust the approach is to adversarial perturbations in the observed data. Here, we study the adversarial robustness of amortized Bayesian inference, focusing on simulation-based estimation of multi-dimensional posterior distributions. We show that almost unrecognizable, targeted perturbations of the observations can lead to drastic changes in the predicted posterior and highly unrealistic posterior predictive samples, across several benchmark tasks and a real-world example from neuroscience. We propose a computationally efficient regularization scheme based on penalizing the Fisher information of the conditional density estimator, and show how it improves the adversarial robustness of amortized Bayesian inference.

Truncated proposals for scalable and hassle-free simulation-based inference

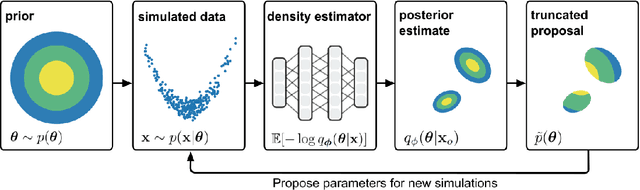
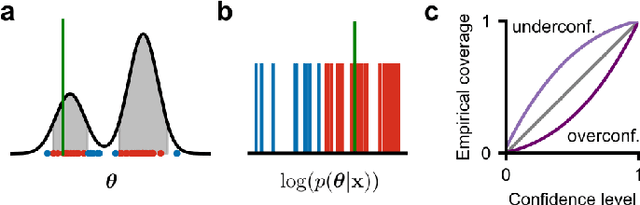
Simulation-based inference (SBI) solves statistical inverse problems by repeatedly running a stochastic simulator and inferring posterior distributions from model-simulations. To improve simulation efficiency, several inference methods take a sequential approach and iteratively adapt the proposal distributions from which model simulations are generated. However, many of these sequential methods are difficult to use in practice, both because the resulting optimisation problems can be challenging and efficient diagnostic tools are lacking. To overcome these issues, we present Truncated Sequential Neural Posterior Estimation (TSNPE). TSNPE performs sequential inference with truncated proposals, sidestepping the optimisation issues of alternative approaches. In addition, TSNPE allows to efficiently perform coverage tests that can scale to complex models with many parameters. We demonstrate that TSNPE performs on par with previous methods on established benchmark tasks. We then apply TSNPE to two challenging problems from neuroscience and show that TSNPE can successfully obtain the posterior distributions, whereas previous methods fail. Overall, our results demonstrate that TSNPE is an efficient, accurate, and robust inference method that can scale to challenging scientific models.

Variational methods for simulation-based inference

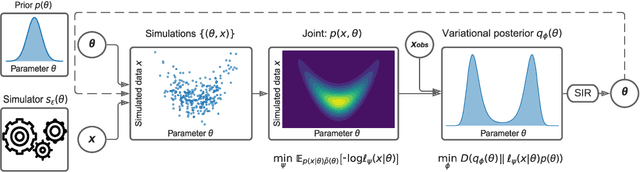
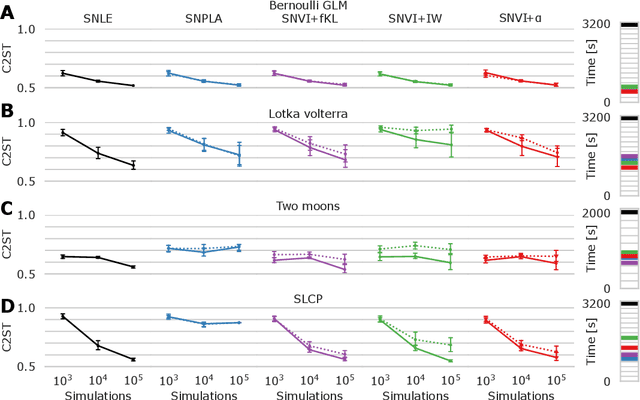
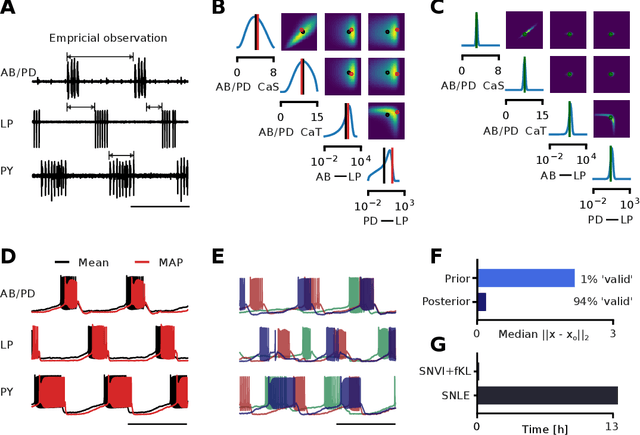
We present Sequential Neural Variational Inference (SNVI), an approach to perform Bayesian inference in models with intractable likelihoods. SNVI combines likelihood-estimation (or likelihood-ratio-estimation) with variational inference to achieve a scalable simulation-based inference approach. SNVI maintains the flexibility of likelihood(-ratio) estimation to allow arbitrary proposals for simulations, while simultaneously providing a functional estimate of the posterior distribution without requiring MCMC sampling. We present several variants of SNVI and demonstrate that they are substantially more computationally efficient than previous algorithms, without loss of accuracy on benchmark tasks. We apply SNVI to a neuroscience model of the pyloric network in the crab and demonstrate that it can infer the posterior distribution with one order of magnitude fewer simulations than previously reported. SNVI vastly reduces the computational cost of simulation-based inference while maintaining accuracy and flexibility, making it possible to tackle problems that were previously inaccessible.

Group equivariant neural posterior estimation

Simulation-based inference with conditional neural density estimators is a powerful approach to solving inverse problems in science. However, these methods typically treat the underlying forward model as a black box, with no way to exploit geometric properties such as equivariances. Equivariances are common in scientific models, however integrating them directly into expressive inference networks (such as normalizing flows) is not straightforward. We here describe an alternative method to incorporate equivariances under joint transformations of parameters and data. Our method -- called group equivariant neural posterior estimation (GNPE) -- is based on self-consistently standardizing the "pose" of the data while estimating the posterior over parameters. It is architecture-independent, and applies both to exact and approximate equivariances. As a real-world application, we use GNPE for amortized inference of astrophysical binary black hole systems from gravitational-wave observations. We show that GNPE achieves state-of-the-art accuracy while reducing inference times by three orders of magnitude.