Learning Curves of Stochastic Gradient Descent in Kernel Regression

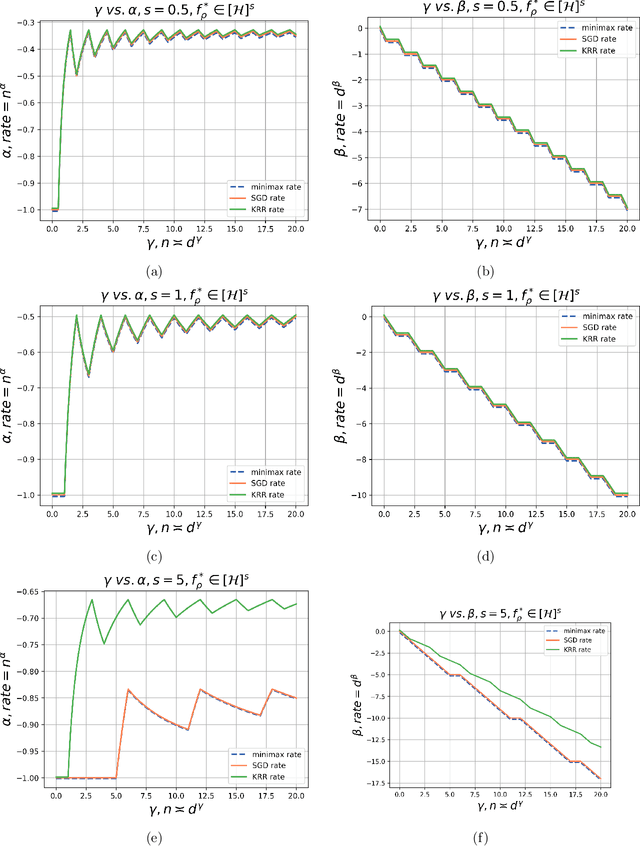
This paper considers a canonical problem in kernel regression: how good are the model performances when it is trained by the popular online first-order algorithms, compared to the offline ones, such as ridge and ridgeless regression? In this paper, we analyze the foundational single-pass Stochastic Gradient Descent (SGD) in kernel regression under source condition where the optimal predictor can even not belong to the RKHS, i.e. the model is misspecified. Specifically, we focus on the inner product kernel over the sphere and characterize the exact orders of the excess risk curves under different scales of sample sizes $n$ concerning the input dimension $d$. Surprisingly, we show that SGD achieves min-max optimal rates up to constants among all the scales, without suffering the saturation, a prevalent phenomenon observed in (ridge) regression, except when the model is highly misspecified and the learning is in a final stage where $n\gg d^{\gamma}$ with any constant $\gamma >0$. The main reason for SGD to overcome the curse of saturation is the exponentially decaying step size schedule, a common practice in deep neural network training. As a byproduct, we provide the \emph{first} provable advantage of the scheme over the iterative averaging method in the common setting.

Scaling Law for Stochastic Gradient Descent in Quadratically Parameterized Linear Regression

In machine learning, the scaling law describes how the model performance improves with the model and data size scaling up. From a learning theory perspective, this class of results establishes upper and lower generalization bounds for a specific learning algorithm. Here, the exact algorithm running using a specific model parameterization often offers a crucial implicit regularization effect, leading to good generalization. To characterize the scaling law, previous theoretical studies mainly focus on linear models, whereas, feature learning, a notable process that contributes to the remarkable empirical success of neural networks, is regretfully vacant. This paper studies the scaling law over a linear regression with the model being quadratically parameterized. We consider infinitely dimensional data and slope ground truth, both signals exhibiting certain power-law decay rates. We study convergence rates for Stochastic Gradient Descent and demonstrate the learning rates for variables will automatically adapt to the ground truth. As a result, in the canonical linear regression, we provide explicit separations for generalization curves between SGD with and without feature learning, and the information-theoretical lower bound that is agnostic to parametrization method and the algorithm. Our analysis for decaying ground truth provides a new characterization for the learning dynamic of the model.

Optimal Algorithms in Linear Regression under Covariate Shift: On the Importance of Precondition

A common pursuit in modern statistical learning is to attain satisfactory generalization out of the source data distribution (OOD). In theory, the challenge remains unsolved even under the canonical setting of covariate shift for the linear model. This paper studies the foundational (high-dimensional) linear regression where the ground truth variables are confined to an ellipse-shape constraint and addresses two fundamental questions in this regime: (i) given the target covariate matrix, what is the min-max \emph{optimal} algorithm under covariate shift? (ii) for what kinds of target classes, the commonly-used SGD-type algorithms achieve optimality? Our analysis starts with establishing a tight lower generalization bound via a Bayesian Cramer-Rao inequality. For (i), we prove that the optimal estimator can be simply a certain linear transformation of the best estimator for the source distribution. Given the source and target matrices, we show that the transformation can be efficiently computed via a convex program. The min-max optimal analysis for SGD leverages the idea that we recognize both the accumulated updates of the applied algorithms and the ideal transformation as preconditions on the learning variables. We provide sufficient conditions when SGD with its acceleration variants attain optimality.

Fundamental Computational Limits in Pursuing Invariant Causal Prediction and Invariance-Guided Regularization

Pursuing invariant prediction from heterogeneous environments opens the door to learning causality in a purely data-driven way and has several applications in causal discovery and robust transfer learning. However, existing methods such as ICP [Peters et al., 2016] and EILLS [Fan et al., 2024] that can attain sample-efficient estimation are based on exponential time algorithms. In this paper, we show that such a problem is intrinsically hard in computation: the decision problem, testing whether a non-trivial prediction-invariant solution exists across two environments, is NP-hard even for the linear causal relationship. In the world where P$\neq$NP, our results imply that the estimation error rate can be arbitrarily slow using any computationally efficient algorithm. This suggests that pursuing causality is fundamentally harder than detecting associations when no prior assumption is pre-offered. Given there is almost no hope of computational improvement under the worst case, this paper proposes a method capable of attaining both computationally and statistically efficient estimation under additional conditions. Furthermore, our estimator is a distributionally robust estimator with an ellipse-shaped uncertain set where more uncertainty is placed on spurious directions than invariant directions, resulting in a smooth interpolation between the most predictive solution and the causal solution by varying the invariance hyper-parameter. Non-asymptotic results and empirical applications support the claim.

The Optimality of (Accelerated) SGD for High-Dimensional Quadratic Optimization

Stochastic gradient descent (SGD) is a widely used algorithm in machine learning, particularly for neural network training. Recent studies on SGD for canonical quadratic optimization or linear regression show it attains well generalization under suitable high-dimensional settings. However, a fundamental question -- for what kinds of high-dimensional learning problems SGD and its accelerated variants can achieve optimality has yet to be well studied. This paper investigates SGD with two essential components in practice: exponentially decaying step size schedule and momentum. We establish the convergence upper bound for momentum accelerated SGD (ASGD) and propose concrete classes of learning problems under which SGD or ASGD achieves min-max optimal convergence rates. The characterization of the target function is based on standard power-law decays in (functional) linear regression. Our results unveil new insights for understanding the learning bias of SGD: (i) SGD is efficient in learning ``dense'' features where the corresponding weights are subject to an infinity norm constraint; (ii) SGD is efficient for easy problem without suffering from the saturation effect; (iii) momentum can accelerate the convergence rate by order when the learning problem is relatively hard. To our knowledge, this is the first work to clearly identify the optimal boundary of SGD versus ASGD for the problem under mild settings.

Relational Learning in Pre-Trained Models: A Theory from Hypergraph Recovery Perspective

Foundation Models (FMs) have demonstrated remarkable insights into the relational dynamics of the world, leading to the crucial question: how do these models acquire an understanding of world hybrid relations? Traditional statistical learning, particularly for prediction problems, may overlook the rich and inherently structured information from the data, especially regarding the relationships between objects. We introduce a mathematical model that formalizes relational learning as hypergraph recovery to study pre-training of FMs. In our framework, the world is represented as a hypergraph, with data abstracted as random samples from hyperedges. We theoretically examine the feasibility of a Pre-Trained Model (PTM) to recover this hypergraph and analyze the data efficiency in a minimax near-optimal style. By integrating rich graph theories into the realm of PTMs, our mathematical framework offers powerful tools for an in-depth understanding of pre-training from a unique perspective and can be used under various scenarios. As an example, we extend the framework to entity alignment in multimodal learning.

On the Algorithmic Bias of Aligning Large Language Models with RLHF: Preference Collapse and Matching Regularization

Accurately aligning large language models (LLMs) with human preferences is crucial for informing fair, economically sound, and statistically efficient decision-making processes. However, we argue that reinforcement learning from human feedback (RLHF) -- the predominant approach for aligning LLMs with human preferences through a reward model -- suffers from an inherent algorithmic bias due to its Kullback--Leibler-based regularization in optimization. In extreme cases, this bias could lead to a phenomenon we term preference collapse, where minority preferences are virtually disregarded. To mitigate this algorithmic bias, we introduce preference matching (PM) RLHF, a novel approach that provably aligns LLMs with the preference distribution of the reward model under the Bradley--Terry--Luce/Plackett--Luce model. Central to our approach is a PM regularizer that takes the form of the negative logarithm of the LLM's policy probability distribution over responses, which helps the LLM balance response diversification and reward maximization. Notably, we obtain this regularizer by solving an ordinary differential equation that is necessary for the PM property. For practical implementation, we introduce a conditional variant of PM RLHF that is tailored to natural language generation. Finally, we empirically validate the effectiveness of conditional PM RLHF through experiments on the OPT-1.3B and Llama-2-7B models, demonstrating a 29% to 41% improvement in alignment with human preferences, as measured by a certain metric, compared to standard RLHF.

Causality Pursuit from Heterogeneous Environments via Neural Adversarial Invariance Learning

Statistics suffers from a fundamental problem, "the curse of endogeneity" -- the regression function, or more broadly the prediction risk minimizer with infinite data, may not be the target we wish to pursue. This is because when complex data are collected from multiple sources, the biases deviated from the interested (causal) association inherited in individuals or sub-populations are not expected to be canceled. Traditional remedies are of hindsight and restrictive in being tailored to prior knowledge like untestable cause-effect structures, resulting in methods that risk model misspecification and lack scalable applicability. This paper seeks to offer a purely data-driven and universally applicable method that only uses the heterogeneity of the biases in the data rather than following pre-offered commandments. Such an idea is formulated as a nonparametric invariance pursuit problem, whose goal is to unveil the invariant conditional expectation $m^\star(x)\equiv \mathbb{E}[Y^{(e)}|X_{S^\star}^{(e)}=x_{S^\star}]$ with unknown important variable set $S^\star$ across heterogeneous environments $e\in \mathcal{E}$. Under the structural causal model framework, $m^\star$ can be interpreted as certain data-driven causality in general. The paper contributes to proposing a novel framework, called Focused Adversarial Invariance Regularization (FAIR), formulated as a single minimax optimization program that can solve the general invariance pursuit problem. As illustrated by the unified non-asymptotic analysis, our adversarial estimation framework can attain provable sample-efficient estimation akin to standard regression under a minimal identification condition for various tasks and models. As an application, the FAIR-NN estimator realized by two Neural Network classes is highlighted as the first approach to attain statistically efficient estimation in general nonparametric invariance learning.

INSIGHT: End-to-End Neuro-Symbolic Visual Reinforcement Learning with Language Explanations

Neuro-symbolic reinforcement learning (NS-RL) has emerged as a promising paradigm for explainable decision-making, characterized by the interpretability of symbolic policies. For tasks with visual observations, NS-RL entails structured representations for states, but previous algorithms are unable to refine the structured states with reward signals due to a lack of efficiency. Accessibility is also an issue, as extensive domain knowledge is required to interpret current symbolic policies. In this paper, we present a framework that is capable of learning structured states and symbolic policies simultaneously, whose key idea is to overcome the efficiency bottleneck by distilling vision foundation models into a scalable perception module. Moreover, we design a pipeline that uses large language models to generate concise and readable language explanations for policies and decisions. In experiments on nine Atari tasks, our approach demonstrates substantial performance gains over existing NSRL methods. We also showcase explanations for policies and decisions.

The Implicit Bias of Heterogeneity towards Invariance and Causality

It is observed empirically that the large language models (LLM), trained with a variant of regression loss using numerous corpus from the Internet, can unveil causal associations to some extent. This is contrary to the traditional wisdom that ``association is not causation'' and the paradigm of traditional causal inference in which prior causal knowledge should be carefully incorporated into the design of methods. It is a mystery why causality, in a higher layer of understanding, can emerge from the regression task that pursues associations. In this paper, we claim the emergence of causality from association-oriented training can be attributed to the coupling effects from the heterogeneity of the source data, stochasticity of training algorithms, and over-parameterization of the learning models. We illustrate such an intuition using a simple but insightful model that learns invariance, a quasi-causality, using regression loss. To be specific, we consider multi-environment low-rank matrix sensing problems where the unknown r-rank ground-truth d*d matrices diverge across the environments but contain a lower-rank invariant, causal part. In this case, running pooled gradient descent will result in biased solutions that only learn associations in general. We show that running large-batch Stochastic Gradient Descent, whose each batch being linear measurement samples randomly selected from a certain environment, can successfully drive the solution towards the invariant, causal solution under certain conditions. This step is related to the relatively strong heterogeneity of the environments, the large step size and noises in the optimization algorithm, and the over-parameterization of the model. In summary, we unveil another implicit bias that is a result of the symbiosis between the heterogeneity of data and modern algorithms, which is, to the best of our knowledge, first in the literature.