Feature Projection Learning for Better Vision-Language Reasoning

Vision-Language Pre-Trained models, notably CLIP, that utilize contrastive learning have proven highly adept at extracting generalizable visual features. To inherit the well-learned knowledge of VLP models for downstream tasks, several approaches aim to adapt them efficiently with limited supervision. However, these methods either suffer from limited performance, excessive learnable parameters, or extended training times, all of which hinder their effectiveness in adapting the CLIP model to downstream tasks. In this work, we propose a simple yet efficient and effective method called \textit{\textbf{F}eature \textbf{P}rojection \textbf{L}earning(FPL)} to address these problems. Specifically, we develop a projection model that projects class prototype features into the query image feature space and reconstructs the query image feature map. The negative average squared reconstruction error is used as the class score. In this way, we transform the classification problem into a feature projection problem. The final output of this method is a combination of the prediction from the projection model and the original pre-trained CLIP. Comprehensive empirical evaluations confirm that FPL delivers superior accuracy, surpassing the current state-of-the-art methods by a substantial margin.

Learning Curves of Stochastic Gradient Descent in Kernel Regression

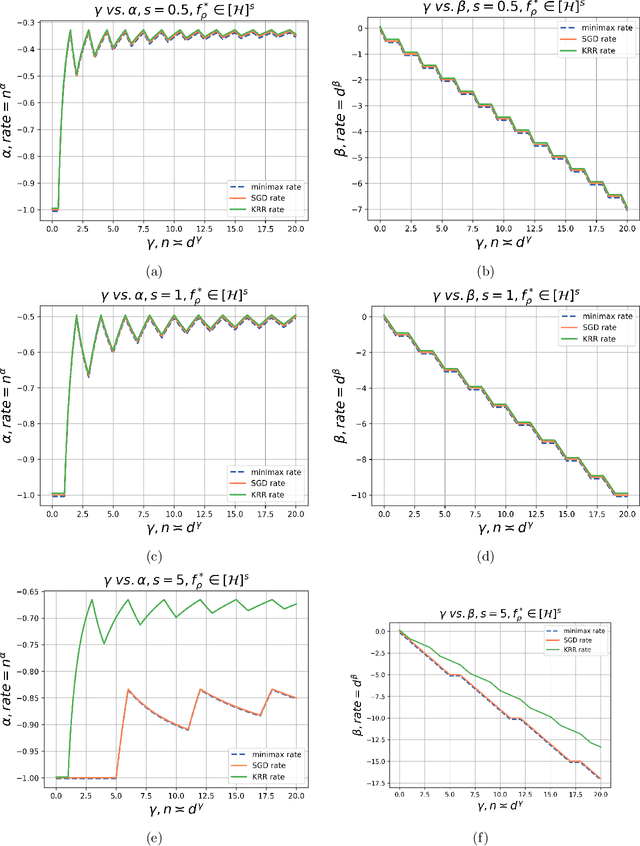
This paper considers a canonical problem in kernel regression: how good are the model performances when it is trained by the popular online first-order algorithms, compared to the offline ones, such as ridge and ridgeless regression? In this paper, we analyze the foundational single-pass Stochastic Gradient Descent (SGD) in kernel regression under source condition where the optimal predictor can even not belong to the RKHS, i.e. the model is misspecified. Specifically, we focus on the inner product kernel over the sphere and characterize the exact orders of the excess risk curves under different scales of sample sizes $n$ concerning the input dimension $d$. Surprisingly, we show that SGD achieves min-max optimal rates up to constants among all the scales, without suffering the saturation, a prevalent phenomenon observed in (ridge) regression, except when the model is highly misspecified and the learning is in a final stage where $n\gg d^{\gamma}$ with any constant $\gamma >0$. The main reason for SGD to overcome the curse of saturation is the exponentially decaying step size schedule, a common practice in deep neural network training. As a byproduct, we provide the \emph{first} provable advantage of the scheme over the iterative averaging method in the common setting.