Learning Curves of Stochastic Gradient Descent in Kernel Regression

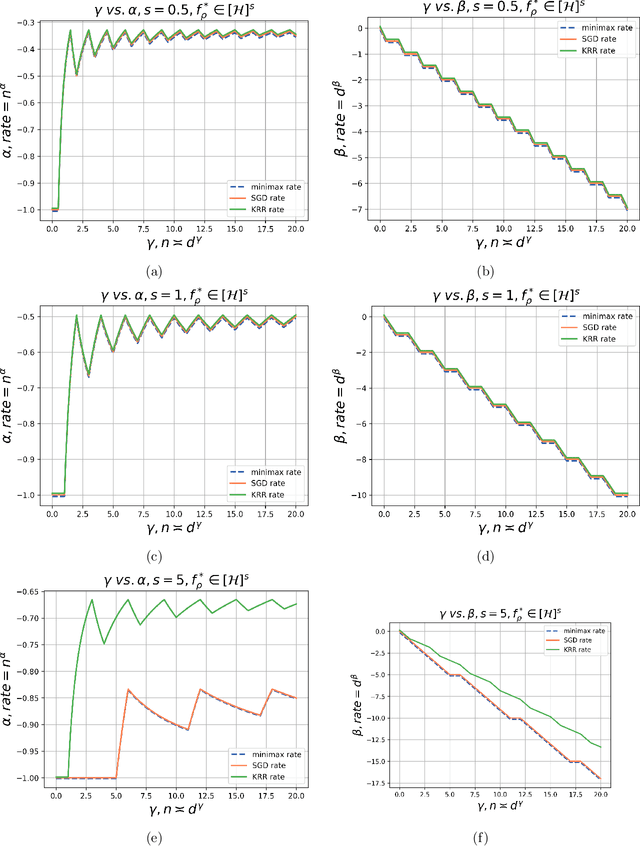
This paper considers a canonical problem in kernel regression: how good are the model performances when it is trained by the popular online first-order algorithms, compared to the offline ones, such as ridge and ridgeless regression? In this paper, we analyze the foundational single-pass Stochastic Gradient Descent (SGD) in kernel regression under source condition where the optimal predictor can even not belong to the RKHS, i.e. the model is misspecified. Specifically, we focus on the inner product kernel over the sphere and characterize the exact orders of the excess risk curves under different scales of sample sizes $n$ concerning the input dimension $d$. Surprisingly, we show that SGD achieves min-max optimal rates up to constants among all the scales, without suffering the saturation, a prevalent phenomenon observed in (ridge) regression, except when the model is highly misspecified and the learning is in a final stage where $n\gg d^{\gamma}$ with any constant $\gamma >0$. The main reason for SGD to overcome the curse of saturation is the exponentially decaying step size schedule, a common practice in deep neural network training. As a byproduct, we provide the \emph{first} provable advantage of the scheme over the iterative averaging method in the common setting.

Scaling Law for Stochastic Gradient Descent in Quadratically Parameterized Linear Regression

In machine learning, the scaling law describes how the model performance improves with the model and data size scaling up. From a learning theory perspective, this class of results establishes upper and lower generalization bounds for a specific learning algorithm. Here, the exact algorithm running using a specific model parameterization often offers a crucial implicit regularization effect, leading to good generalization. To characterize the scaling law, previous theoretical studies mainly focus on linear models, whereas, feature learning, a notable process that contributes to the remarkable empirical success of neural networks, is regretfully vacant. This paper studies the scaling law over a linear regression with the model being quadratically parameterized. We consider infinitely dimensional data and slope ground truth, both signals exhibiting certain power-law decay rates. We study convergence rates for Stochastic Gradient Descent and demonstrate the learning rates for variables will automatically adapt to the ground truth. As a result, in the canonical linear regression, we provide explicit separations for generalization curves between SGD with and without feature learning, and the information-theoretical lower bound that is agnostic to parametrization method and the algorithm. Our analysis for decaying ground truth provides a new characterization for the learning dynamic of the model.

Optimal Algorithms in Linear Regression under Covariate Shift: On the Importance of Precondition

A common pursuit in modern statistical learning is to attain satisfactory generalization out of the source data distribution (OOD). In theory, the challenge remains unsolved even under the canonical setting of covariate shift for the linear model. This paper studies the foundational (high-dimensional) linear regression where the ground truth variables are confined to an ellipse-shape constraint and addresses two fundamental questions in this regime: (i) given the target covariate matrix, what is the min-max \emph{optimal} algorithm under covariate shift? (ii) for what kinds of target classes, the commonly-used SGD-type algorithms achieve optimality? Our analysis starts with establishing a tight lower generalization bound via a Bayesian Cramer-Rao inequality. For (i), we prove that the optimal estimator can be simply a certain linear transformation of the best estimator for the source distribution. Given the source and target matrices, we show that the transformation can be efficiently computed via a convex program. The min-max optimal analysis for SGD leverages the idea that we recognize both the accumulated updates of the applied algorithms and the ideal transformation as preconditions on the learning variables. We provide sufficient conditions when SGD with its acceleration variants attain optimality.

The Optimality of (Accelerated) SGD for High-Dimensional Quadratic Optimization

Stochastic gradient descent (SGD) is a widely used algorithm in machine learning, particularly for neural network training. Recent studies on SGD for canonical quadratic optimization or linear regression show it attains well generalization under suitable high-dimensional settings. However, a fundamental question -- for what kinds of high-dimensional learning problems SGD and its accelerated variants can achieve optimality has yet to be well studied. This paper investigates SGD with two essential components in practice: exponentially decaying step size schedule and momentum. We establish the convergence upper bound for momentum accelerated SGD (ASGD) and propose concrete classes of learning problems under which SGD or ASGD achieves min-max optimal convergence rates. The characterization of the target function is based on standard power-law decays in (functional) linear regression. Our results unveil new insights for understanding the learning bias of SGD: (i) SGD is efficient in learning ``dense'' features where the corresponding weights are subject to an infinity norm constraint; (ii) SGD is efficient for easy problem without suffering from the saturation effect; (iii) momentum can accelerate the convergence rate by order when the learning problem is relatively hard. To our knowledge, this is the first work to clearly identify the optimal boundary of SGD versus ASGD for the problem under mild settings.