A Unifying View of Linear Function Approximation in Off-Policy RL Through Matrix Splitting and Preconditioning

Traditionally, TD and FQI are viewed as differing in the number of updates toward the target value function: TD makes one update, FQI makes an infinite number, and Partial Fitted Q-Iteration (PFQI) performs a finite number, such as the use of a target network in Deep Q-Networks (DQN) in the OPE setting. This perspective, however, fails to capture the convergence connections between these algorithms and may lead to incorrect conclusions, for example, that the convergence of TD implies the convergence of FQI. In this paper, we focus on linear value function approximation and offer a new perspective, unifying TD, FQI, and PFQI as the same iterative method for solving the Least Squares Temporal Difference (LSTD) system, but using different preconditioners and matrix splitting schemes. TD uses a constant preconditioner, FQI employs a data-feature adaptive preconditioner, and PFQI transitions between the two. Then, we reveal that in the context of linear function approximation, increasing the number of updates under the same target value function essentially represents a transition from using a constant preconditioner to data-feature adaptive preconditioner. This unifying perspective also simplifies the analyses of the convergence conditions for these algorithms and clarifies many issues. Consequently, we fully characterize the convergence of each algorithm without assuming specific properties of the chosen features (e.g., linear independence). We also examine how common assumptions about feature representations affect convergence, and discover new conditions on features that are important for convergence. These convergence conditions allow us to establish the convergence connections between these algorithms and to address important questions.

Amazing Things Come From Having Many Good Models

The Rashomon Effect, coined by Leo Breiman, describes the phenomenon that there exist many equally good predictive models for the same dataset. This phenomenon happens for many real datasets and when it does, it sparks both magic and consternation, but mostly magic. In light of the Rashomon Effect, this perspective piece proposes reshaping the way we think about machine learning, particularly for tabular data problems in the nondeterministic (noisy) setting. We address how the Rashomon Effect impacts (1) the existence of simple-yet-accurate models, (2) flexibility to address user preferences, such as fairness and monotonicity, without losing performance, (3) uncertainty in predictions, fairness, and explanations, (4) reliable variable importance, (5) algorithm choice, specifically, providing advanced knowledge of which algorithms might be suitable for a given problem, and (6) public policy. We also discuss a theory of when the Rashomon Effect occurs and why. Our goal is to illustrate how the Rashomon Effect can have a massive impact on the use of machine learning for complex problems in society.

Mitigating Partial Observability in Sequential Decision Processes via the Lambda Discrepancy

Reinforcement learning algorithms typically rely on the assumption that the environment dynamics and value function can be expressed in terms of a Markovian state representation. However, when state information is only partially observable, how can an agent learn such a state representation, and how can it detect when it has found one? We introduce a metric that can accomplish both objectives, without requiring access to--or knowledge of--an underlying, unobservable state space. Our metric, the $\lambda$-discrepancy, is the difference between two distinct temporal difference (TD) value estimates, each computed using TD($\lambda$) with a different value of $\lambda$. Since TD($\lambda$=0) makes an implicit Markov assumption and TD($\lambda$=1) does not, a discrepancy between these estimates is a potential indicator of a non-Markovian state representation. Indeed, we prove that the $\lambda$-discrepancy is exactly zero for all Markov decision processes and almost always non-zero for a broad class of partially observable environments. We also demonstrate empirically that, once detected, minimizing the $\lambda$-discrepancy can help with learning a memory function to mitigate the corresponding partial observability. We then train a reinforcement learning agent that simultaneously constructs two recurrent value networks with different $\lambda$ parameters and minimizes the difference between them as an auxiliary loss. The approach scales to challenging partially observable domains, where the resulting agent frequently performs significantly better (and never performs worse) than a baseline recurrent agent with only a single value network.

An Optimal Tightness Bound for the Simulation Lemma

We present a bound for value-prediction error with respect to model misspecification that is tight, including constant factors. This is a direct improvement of the "simulation lemma," a foundational result in reinforcement learning. We demonstrate that existing bounds are quite loose, becoming vacuous for large discount factors, due to the suboptimal treatment of compounding probability errors. By carefully considering this quantity on its own, instead of as a subcomponent of value error, we derive a bound that is sub-linear with respect to transition function misspecification. We then demonstrate broader applicability of this technique, improving a similar bound in the related subfield of hierarchical abstraction.

A Path to Simpler Models Starts With Noise

The Rashomon set is the set of models that perform approximately equally well on a given dataset, and the Rashomon ratio is the fraction of all models in a given hypothesis space that are in the Rashomon set. Rashomon ratios are often large for tabular datasets in criminal justice, healthcare, lending, education, and in other areas, which has practical implications about whether simpler models can attain the same level of accuracy as more complex models. An open question is why Rashomon ratios often tend to be large. In this work, we propose and study a mechanism of the data generation process, coupled with choices usually made by the analyst during the learning process, that determines the size of the Rashomon ratio. Specifically, we demonstrate that noisier datasets lead to larger Rashomon ratios through the way that practitioners train models. Additionally, we introduce a measure called pattern diversity, which captures the average difference in predictions between distinct classification patterns in the Rashomon set, and motivate why it tends to increase with label noise. Our results explain a key aspect of why simpler models often tend to perform as well as black box models on complex, noisier datasets.

Fitted Q-Learning for Relational Domains

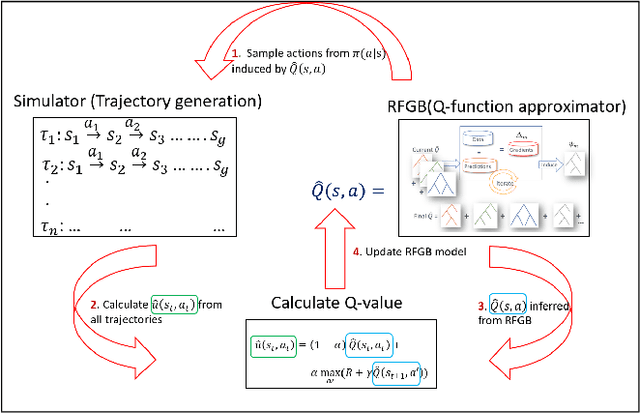
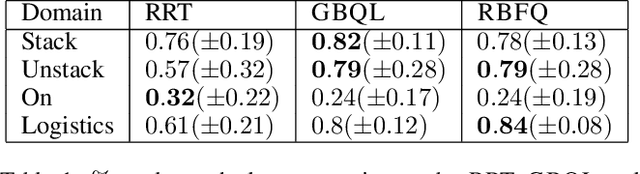
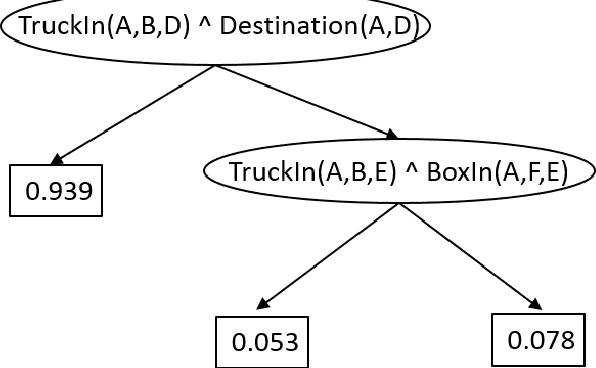
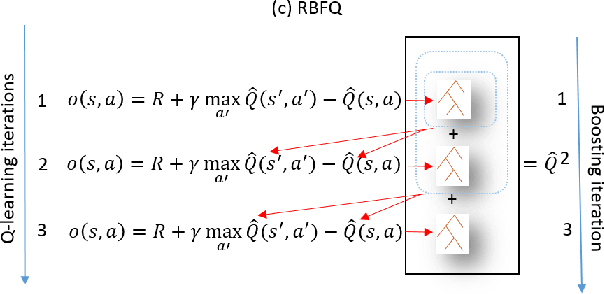
We consider the problem of Approximate Dynamic Programming in relational domains. Inspired by the success of fitted Q-learning methods in propositional settings, we develop the first relational fitted Q-learning algorithms by representing the value function and Bellman residuals. When we fit the Q-functions, we show how the two steps of Bellman operator; application and projection steps can be performed using a gradient-boosting technique. Our proposed framework performs reasonably well on standard domains without using domain models and using fewer training trajectories.

Proceedings of the Twenty-Third Conference on Uncertainty in Artificial Intelligence

This is the Proceedings of the Twenty-Third Conference on Uncertainty in Artificial Intelligence, which was held in Vancouver, British Columbia, July 19 - 22 2007.

Greedy Algorithms for Sparse Reinforcement Learning

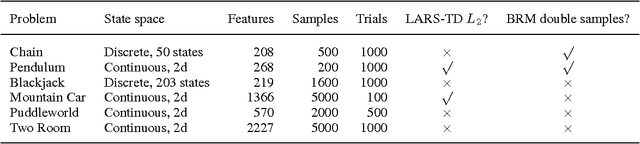
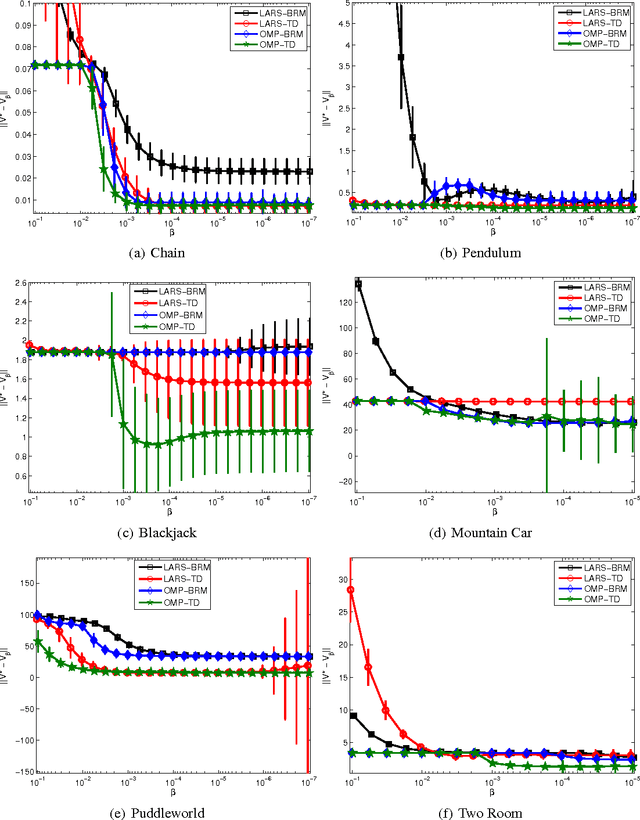
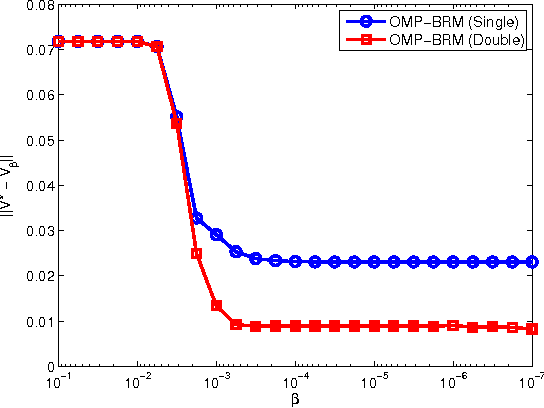
Feature selection and regularization are becoming increasingly prominent tools in the efforts of the reinforcement learning (RL) community to expand the reach and applicability of RL. One approach to the problem of feature selection is to impose a sparsity-inducing form of regularization on the learning method. Recent work on $L_1$ regularization has adapted techniques from the supervised learning literature for use with RL. Another approach that has received renewed attention in the supervised learning community is that of using a simple algorithm that greedily adds new features. Such algorithms have many of the good properties of the $L_1$ regularization methods, while also being extremely efficient and, in some cases, allowing theoretical guarantees on recovery of the true form of a sparse target function from sampled data. This paper considers variants of orthogonal matching pursuit (OMP) applied to reinforcement learning. The resulting algorithms are analyzed and compared experimentally with existing $L_1$ regularized approaches. We demonstrate that perhaps the most natural scenario in which one might hope to achieve sparse recovery fails; however, one variant, OMP-BRM, provides promising theoretical guarantees under certain assumptions on the feature dictionary. Another variant, OMP-TD, empirically outperforms prior methods both in approximation accuracy and efficiency on several benchmark problems.