Mitigating Partial Observability in Sequential Decision Processes via the Lambda Discrepancy

Reinforcement learning algorithms typically rely on the assumption that the environment dynamics and value function can be expressed in terms of a Markovian state representation. However, when state information is only partially observable, how can an agent learn such a state representation, and how can it detect when it has found one? We introduce a metric that can accomplish both objectives, without requiring access to--or knowledge of--an underlying, unobservable state space. Our metric, the $\lambda$-discrepancy, is the difference between two distinct temporal difference (TD) value estimates, each computed using TD($\lambda$) with a different value of $\lambda$. Since TD($\lambda$=0) makes an implicit Markov assumption and TD($\lambda$=1) does not, a discrepancy between these estimates is a potential indicator of a non-Markovian state representation. Indeed, we prove that the $\lambda$-discrepancy is exactly zero for all Markov decision processes and almost always non-zero for a broad class of partially observable environments. We also demonstrate empirically that, once detected, minimizing the $\lambda$-discrepancy can help with learning a memory function to mitigate the corresponding partial observability. We then train a reinforcement learning agent that simultaneously constructs two recurrent value networks with different $\lambda$ parameters and minimizes the difference between them as an auxiliary loss. The approach scales to challenging partially observable domains, where the resulting agent frequently performs significantly better (and never performs worse) than a baseline recurrent agent with only a single value network.

An Optimal Tightness Bound for the Simulation Lemma

We present a bound for value-prediction error with respect to model misspecification that is tight, including constant factors. This is a direct improvement of the "simulation lemma," a foundational result in reinforcement learning. We demonstrate that existing bounds are quite loose, becoming vacuous for large discount factors, due to the suboptimal treatment of compounding probability errors. By carefully considering this quantity on its own, instead of as a subcomponent of value error, we derive a bound that is sub-linear with respect to transition function misspecification. We then demonstrate broader applicability of this technique, improving a similar bound in the related subfield of hierarchical abstraction.

Flipping Coins to Estimate Pseudocounts for Exploration in Reinforcement Learning

We propose a new method for count-based exploration in high-dimensional state spaces. Unlike previous work which relies on density models, we show that counts can be derived by averaging samples from the Rademacher distribution (or coin flips). This insight is used to set up a simple supervised learning objective which, when optimized, yields a state's visitation count. We show that our method is significantly more effective at deducing ground-truth visitation counts than previous work; when used as an exploration bonus for a model-free reinforcement learning algorithm, it outperforms existing approaches on most of 9 challenging exploration tasks, including the Atari game Montezuma's Revenge.

Coarse-Grained Smoothness for RL in Metric Spaces

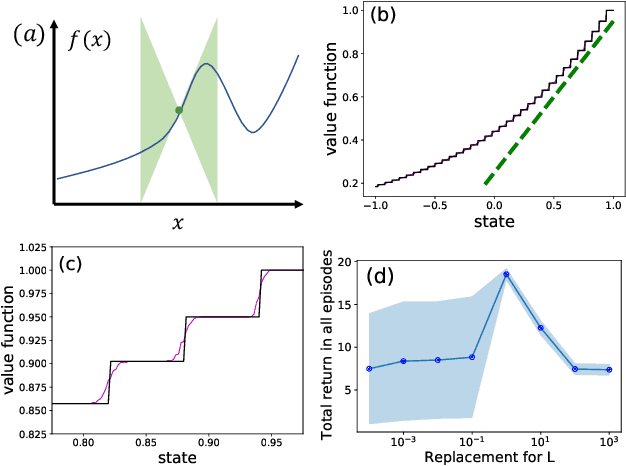
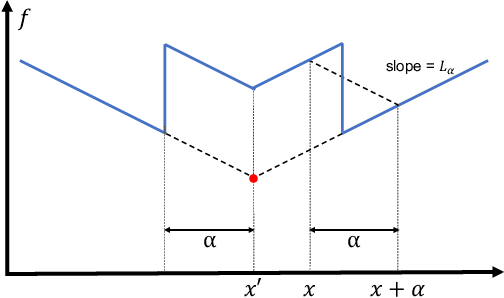
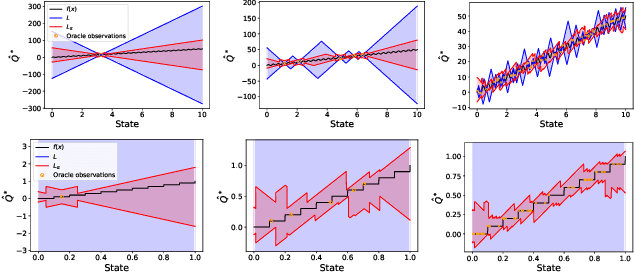
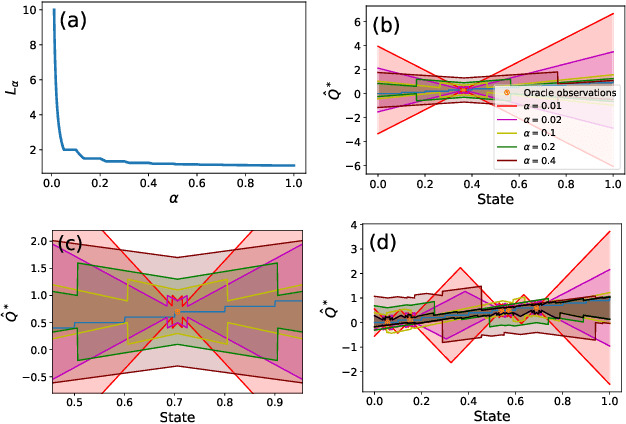
Principled decision-making in continuous state--action spaces is impossible without some assumptions. A common approach is to assume Lipschitz continuity of the Q-function. We show that, unfortunately, this property fails to hold in many typical domains. We propose a new coarse-grained smoothness definition that generalizes the notion of Lipschitz continuity, is more widely applicable, and allows us to compute significantly tighter bounds on Q-functions, leading to improved learning. We provide a theoretical analysis of our new smoothness definition, and discuss its implications and impact on control and exploration in continuous domains.

Towards Amortized Ranking-Critical Training for Collaborative Filtering

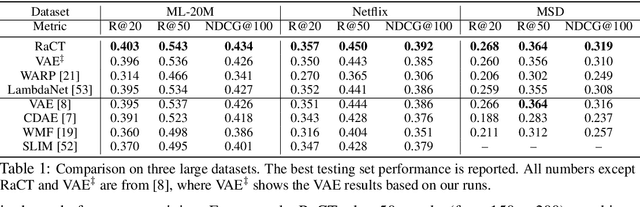
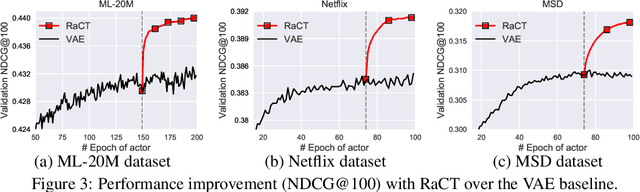
Collaborative filtering is widely used in modern recommender systems. Recent research shows that variational autoencoders (VAEs) yield state-of-the-art performance by integrating flexible representations from deep neural networks into latent variable models, mitigating limitations of traditional linear factor models. VAEs are typically trained by maximizing the likelihood (MLE) of users interacting with ground-truth items. While simple and often effective, MLE-based training does not directly maximize the recommendation-quality metrics one typically cares about, such as top-N ranking. In this paper we investigate new methods for training collaborative filtering models based on actor-critic reinforcement learning, to directly optimize the non-differentiable quality metrics of interest. Specifically, we train a critic network to approximate ranking-based metrics, and then update the actor network (represented here by a VAE) to directly optimize against the learned metrics. In contrast to traditional learning-to-rank methods that require to re-run the optimization procedure for new lists, our critic-based method amortizes the scoring process with a neural network, and can directly provide the (approximate) ranking scores for new lists. Empirically, we show that the proposed methods outperform several state-of-the-art baselines, including recently-proposed deep learning approaches, on three large-scale real-world datasets. The code to reproduce the experimental results and figure plots is on Github: https://github.com/samlobel/RaCT_CF