Explaining black box text modules in natural language with language models

Large language models (LLMs) have demonstrated remarkable prediction performance for a growing array of tasks. However, their rapid proliferation and increasing opaqueness have created a growing need for interpretability. Here, we ask whether we can automatically obtain natural language explanations for black box text modules. A "text module" is any function that maps text to a scalar continuous value, such as a submodule within an LLM or a fitted model of a brain region. "Black box" indicates that we only have access to the module's inputs/outputs. We introduce Summarize and Score (SASC), a method that takes in a text module and returns a natural language explanation of the module's selectivity along with a score for how reliable the explanation is. We study SASC in 3 contexts. First, we evaluate SASC on synthetic modules and find that it often recovers ground truth explanations. Second, we use SASC to explain modules found within a pre-trained BERT model, enabling inspection of the model's internals. Finally, we show that SASC can generate explanations for the response of individual fMRI voxels to language stimuli, with potential applications to fine-grained brain mapping. All code for using SASC and reproducing results is made available on Github.

Bridging Discrete and Backpropagation: Straight-Through and Beyond

Backpropagation, the cornerstone of deep learning, is limited to computing gradients solely for continuous variables. This limitation hinders various research on problems involving discrete latent variables. To address this issue, we propose a novel approach for approximating the gradient of parameters involved in generating discrete latent variables. First, we examine the widely used Straight-Through (ST) heuristic and demonstrate that it works as a first-order approximation of the gradient. Guided by our findings, we propose a novel method called ReinMax, which integrates Heun's Method, a second-order numerical method for solving ODEs, to approximate the gradient. Our method achieves second-order accuracy without requiring Hessian or other second-order derivatives. We conduct experiments on structured output prediction and unsupervised generative modeling tasks. Our results show that \ours brings consistent improvements over the state of the art, including ST and Straight-Through Gumbel-Softmax. Implementations are released at https://github.com/microsoft/ReinMax.

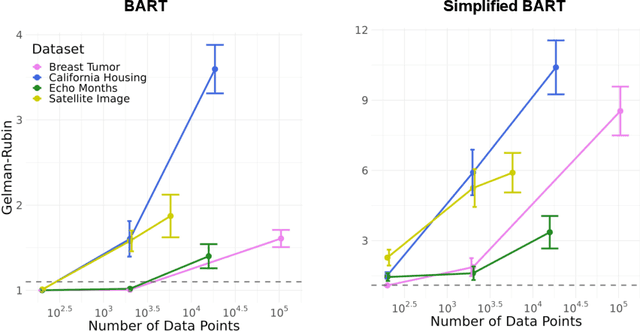
A Mixing Time Lower Bound for a Simplified Version of BART

Bayesian Additive Regression Trees (BART) is a popular Bayesian non-parametric regression algorithm. The posterior is a distribution over sums of decision trees, and predictions are made by averaging approximate samples from the posterior. The combination of strong predictive performance and the ability to provide uncertainty measures has led BART to be commonly used in the social sciences, biostatistics, and causal inference. BART uses Markov Chain Monte Carlo (MCMC) to obtain approximate posterior samples over a parameterized space of sums of trees, but it has often been observed that the chains are slow to mix. In this paper, we provide the first lower bound on the mixing time for a simplified version of BART in which we reduce the sum to a single tree and use a subset of the possible moves for the MCMC proposal distribution. Our lower bound for the mixing time grows exponentially with the number of data points. Inspired by this new connection between the mixing time and the number of data points, we perform rigorous simulations on BART. We show qualitatively that BART's mixing time increases with the number of data points. The slow mixing time of the simplified BART suggests a large variation between different runs of the simplified BART algorithm and a similar large variation is known for BART in the literature. This large variation could result in a lack of stability in the models, predictions, and posterior intervals obtained from the BART MCMC samples. Our lower bound and simulations suggest increasing the number of chains with the number of data points.

SOFFLFM: Super-resolution optical fluctuation Fourier light-field microscopy

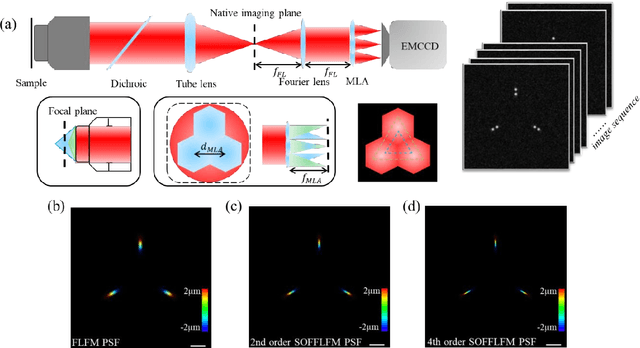
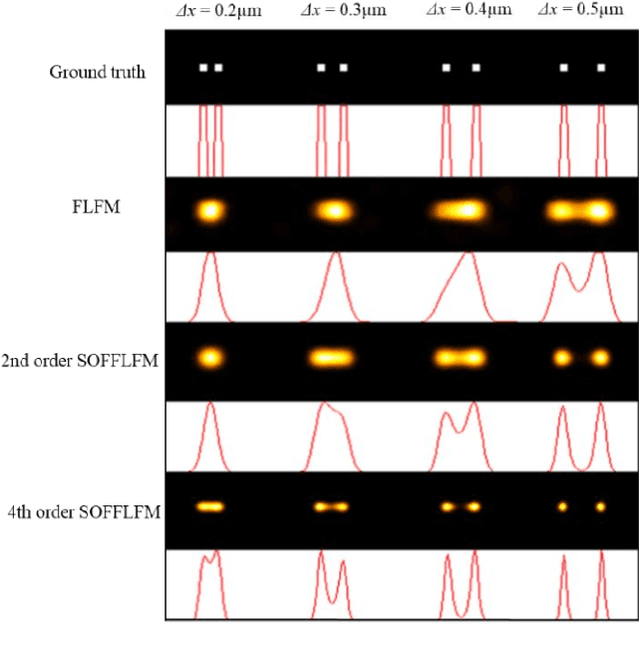
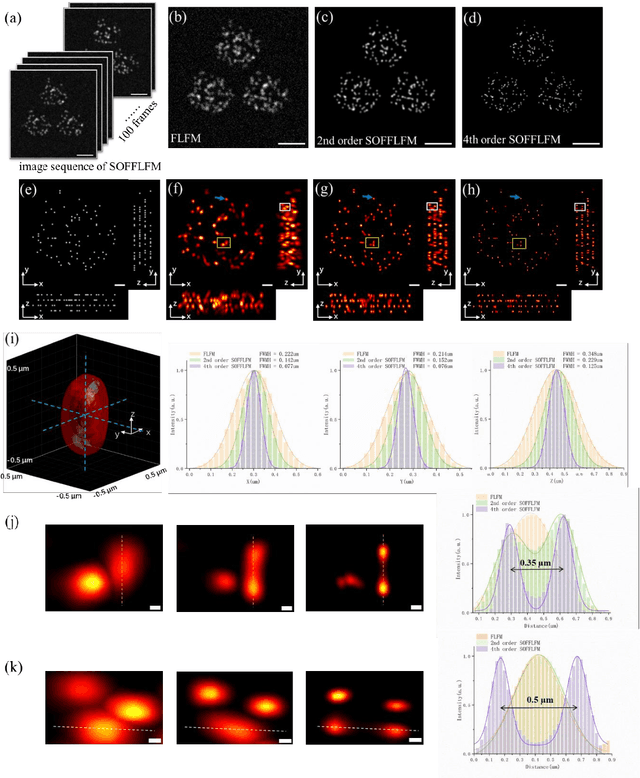
Fourier light-field microscopy (FLFM) uses a micro-lens array (MLA) to segment the Fourier Plane of the microscopic objective lens to generate multiple two-dimensional perspective views, thereby reconstructing the three-dimensional(3D) structure of the sample using 3D deconvolution calculation without scanning. However, the resolution of FLFM is still limited by diffraction, and furthermore, dependent on the aperture division. In order to improve its resolution, a Super-resolution optical fluctuation Fourier light field microscopy (SOFFLFM) was proposed here, in which the Sofi method with ability of super-resolution was introduced into FLFM. SOFFLFM uses higher-order cumulants statistical analysis on an image sequence collected by FLFM, and then carries out 3D deconvolution calculation to reconstruct the 3D structure of the sample. Theoretical basis of SOFFLFM on improving resolution was explained and then verified with simulations. Simulation results demonstrated that SOFFLFM improved lateral and axial resolution by more than sqrt(2) and 2 times in the 2nd and 4th order accumulations, compared with that of FLFM.

Learning Using Privileged Information for Zero-Shot Action Recognition

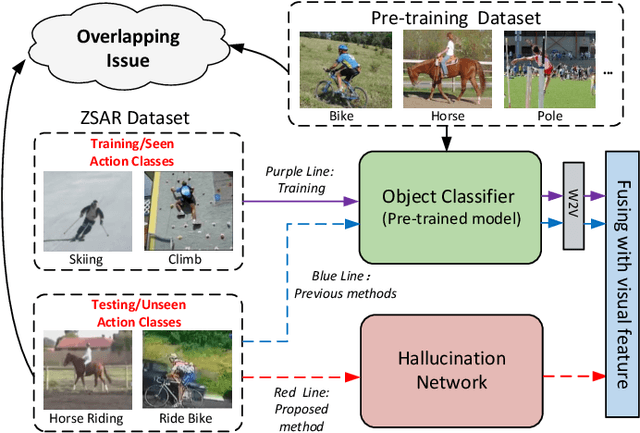
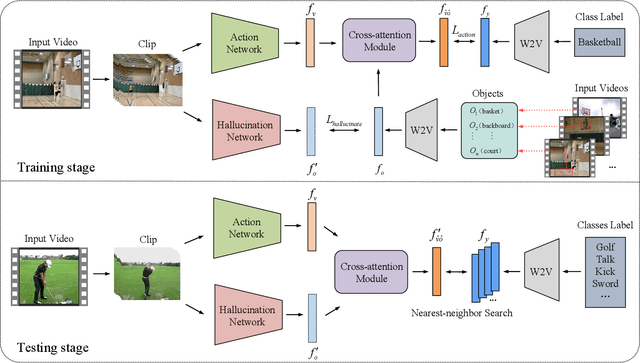
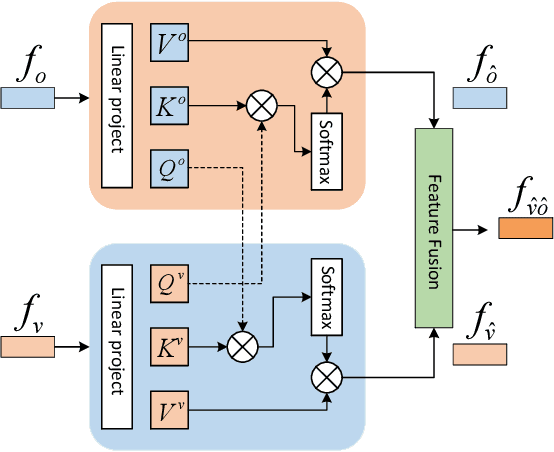
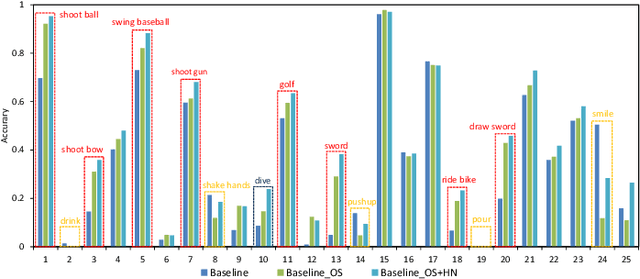
Zero-Shot Action Recognition (ZSAR) aims to recognize video actions that have never been seen during training. Most existing methods assume a shared semantic space between seen and unseen actions and intend to directly learn a mapping from a visual space to the semantic space. This approach has been challenged by the semantic gap between the visual space and semantic space. This paper presents a novel method that uses object semantics as privileged information to narrow the semantic gap and, hence, effectively, assist the learning. In particular, a simple hallucination network is proposed to implicitly extract object semantics during testing without explicitly extracting objects and a cross-attention module is developed to augment visual feature with the object semantics. Experiments on the Olympic Sports, HMDB51 and UCF101 datasets have shown that the proposed method outperforms the state-of-the-art methods by a large margin.

Group Probability-Weighted Tree Sums for Interpretable Modeling of Heterogeneous Data

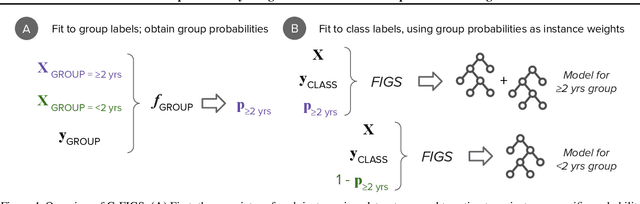
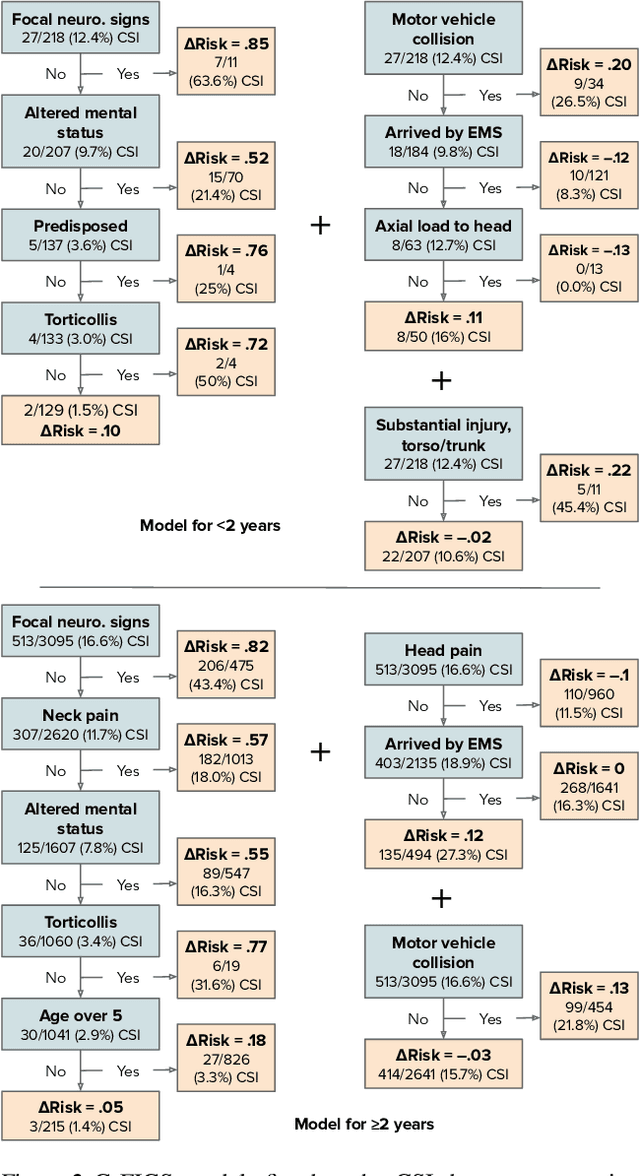
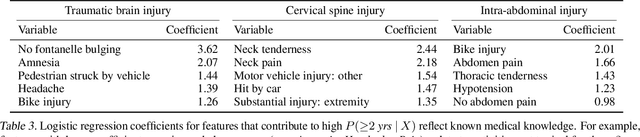
Machine learning in high-stakes domains, such as healthcare, faces two critical challenges: (1) generalizing to diverse data distributions given limited training data while (2) maintaining interpretability. To address these challenges, we propose an instance-weighted tree-sum method that effectively pools data across diverse groups to output a concise, rule-based model. Given distinct groups of instances in a dataset (e.g., medical patients grouped by age or treatment site), our method first estimates group membership probabilities for each instance. Then, it uses these estimates as instance weights in FIGS (Tan et al. 2022), to grow a set of decision trees whose values sum to the final prediction. We call this new method Group Probability-Weighted Tree Sums (G-FIGS). G-FIGS achieves state-of-the-art prediction performance on important clinical datasets; e.g., holding the level of sensitivity fixed at 92%, G-FIGS increases specificity for identifying cervical spine injury by up to 10% over CART and up to 3% over FIGS alone, with larger gains at higher sensitivity levels. By keeping the total number of rules below 16 in FIGS, the final models remain interpretable, and we find that their rules match medical domain expertise. All code, data, and models are released on Github.

Fast Interpretable Greedy-Tree Sums (FIGS)

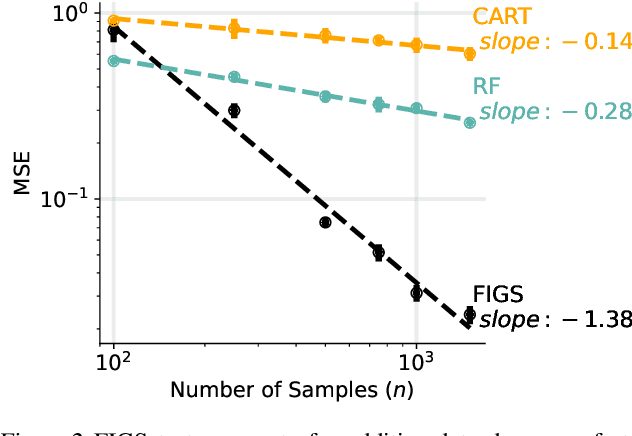
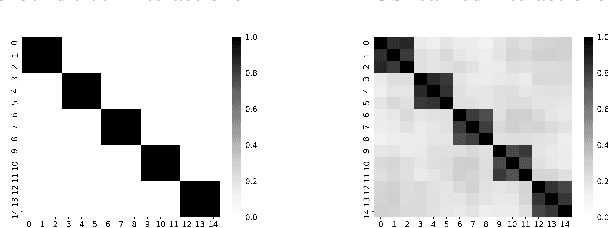
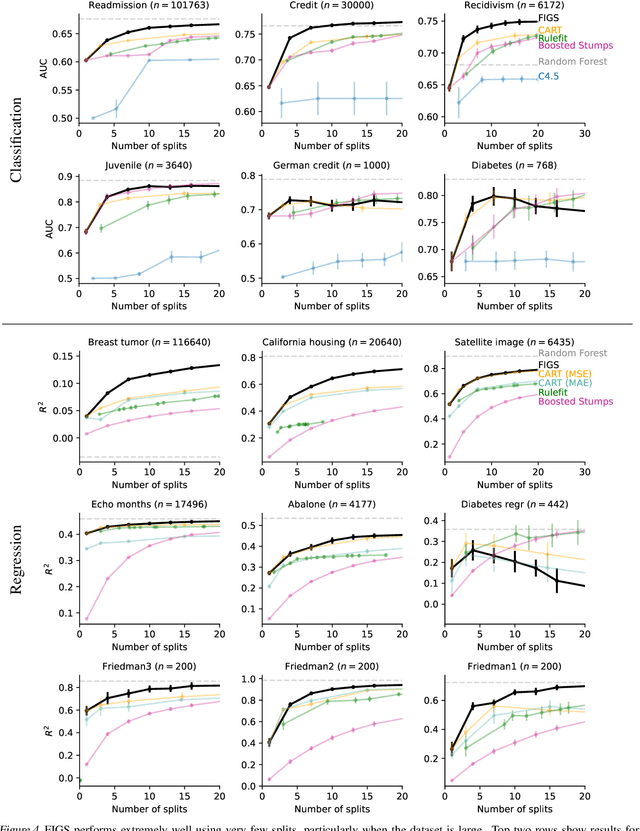
Modern machine learning has achieved impressive prediction performance, but often sacrifices interpretability, a critical consideration in many problems. Here, we propose Fast Interpretable Greedy-Tree Sums (FIGS), an algorithm for fitting concise rule-based models. Specifically, FIGS generalizes the CART algorithm to simultaneously grow a flexible number of trees in a summation. The total number of splits across all the trees can be restricted by a pre-specified threshold, thereby keeping both the size and number of its trees under control. When both are small, the fitted tree-sum can be easily visualized and written out by hand, making it highly interpretable. A partially oracle theoretical result hints at the potential for FIGS to overcome a key weakness of single-tree models by disentangling additive components of generative additive models, thereby reducing redundancy from repeated splits on the same feature. Furthermore, given oracle access to optimal tree structures, we obtain L2 generalization bounds for such generative models in the case of C1 component functions, matching known minimax rates in some cases. Extensive experiments across a wide array of real-world datasets show that FIGS achieves state-of-the-art prediction performance (among all popular rule-based methods) when restricted to just a few splits (e.g. less than 20). We find empirically that FIGS is able to avoid repeated splits, and often provides more concise decision rules than fitted decision trees, without sacrificing predictive performance. All code and models are released in a full-fledged package on Github \url{https://github.com/csinva/imodels}.

Hierarchical Shrinkage: improving the accuracy and interpretability of tree-based methods

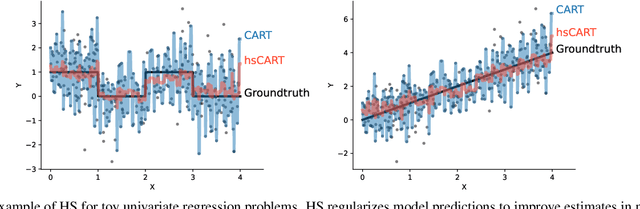
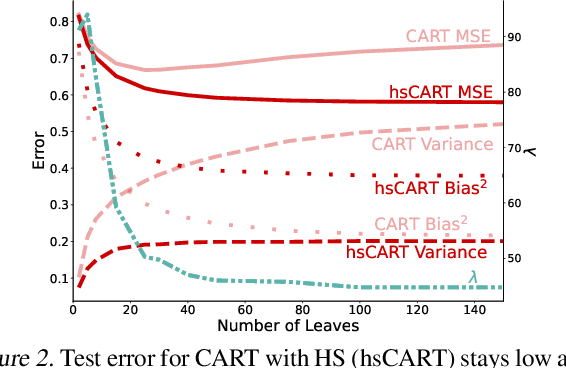
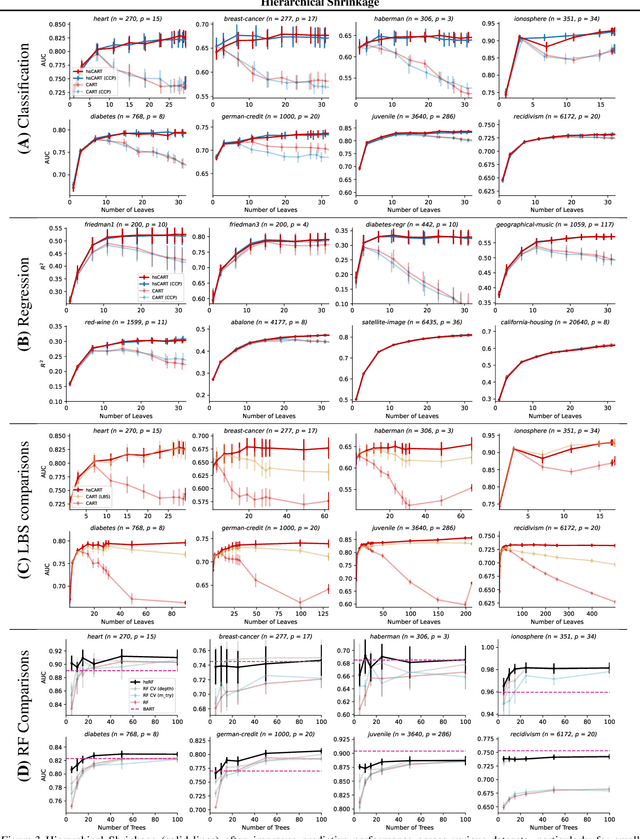
Tree-based models such as decision trees and random forests (RF) are a cornerstone of modern machine-learning practice. To mitigate overfitting, trees are typically regularized by a variety of techniques that modify their structure (e.g. pruning). We introduce Hierarchical Shrinkage (HS), a post-hoc algorithm that does not modify the tree structure, and instead regularizes the tree by shrinking the prediction over each node towards the sample means of its ancestors. The amount of shrinkage is controlled by a single regularization parameter and the number of data points in each ancestor. Since HS is a post-hoc method, it is extremely fast, compatible with any tree growing algorithm, and can be used synergistically with other regularization techniques. Extensive experiments over a wide variety of real-world datasets show that HS substantially increases the predictive performance of decision trees, even when used in conjunction with other regularization techniques. Moreover, we find that applying HS to each tree in an RF often improves accuracy, as well as its interpretability by simplifying and stabilizing its decision boundaries and SHAP values. We further explain the success of HS in improving prediction performance by showing its equivalence to ridge regression on a (supervised) basis constructed of decision stumps associated with the internal nodes of a tree. All code and models are released in a full-fledged package available on Github (github.com/csinva/imodels)

The Three Stages of Learning Dynamics in High-Dimensional Kernel Methods

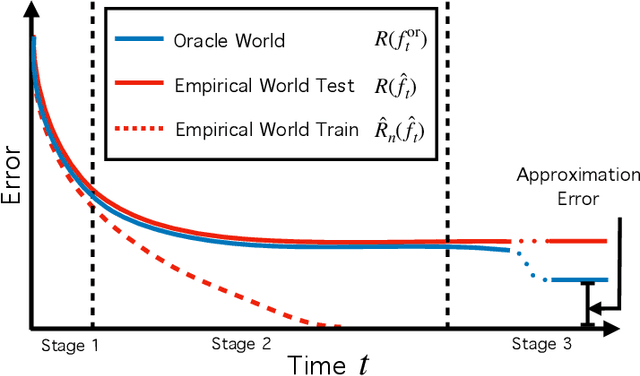
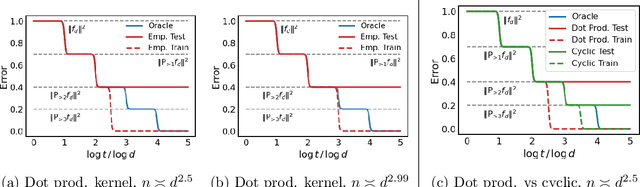
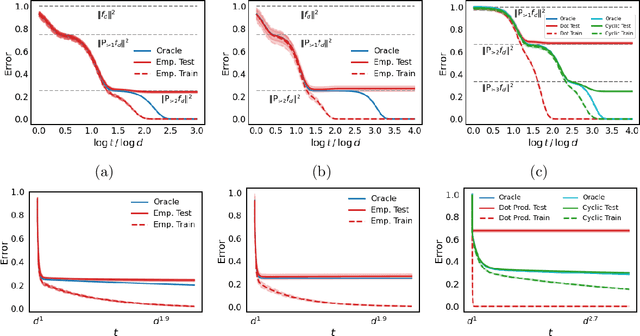
To understand how deep learning works, it is crucial to understand the training dynamics of neural networks. Several interesting hypotheses about these dynamics have been made based on empirically observed phenomena, but there exists a limited theoretical understanding of when and why such phenomena occur. In this paper, we consider the training dynamics of gradient flow on kernel least-squares objectives, which is a limiting dynamics of SGD trained neural networks. Using precise high-dimensional asymptotics, we characterize the dynamics of the fitted model in two "worlds": in the Oracle World the model is trained on the population distribution and in the Empirical World the model is trained on a sampled dataset. We show that under mild conditions on the kernel and $L^2$ target regression function the training dynamics undergo three stages characterized by the behaviors of the models in the two worlds. Our theoretical results also mathematically formalize some interesting deep learning phenomena. Specifically, in our setting we show that SGD progressively learns more complex functions and that there is a "deep bootstrap" phenomenon: during the second stage, the test error of both worlds remain close despite the empirical training error being much smaller. Finally, we give a concrete example comparing the dynamics of two different kernels which shows that faster training is not necessary for better generalization.

A cautionary tale on fitting decision trees to data from additive models: generalization lower bounds

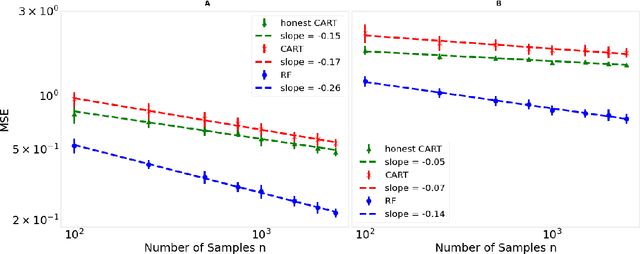
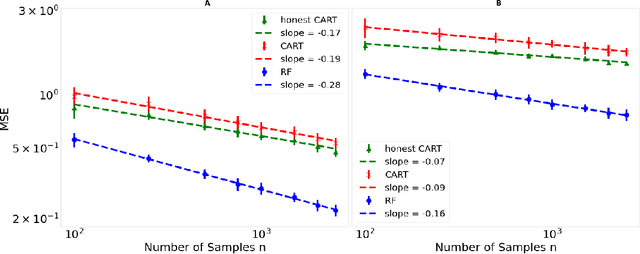
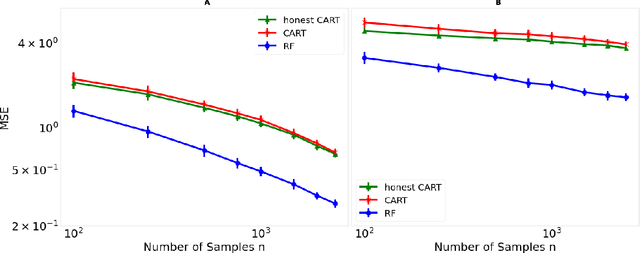
Decision trees are important both as interpretable models amenable to high-stakes decision-making, and as building blocks of ensemble methods such as random forests and gradient boosting. Their statistical properties, however, are not well understood. The most cited prior works have focused on deriving pointwise consistency guarantees for CART in a classical nonparametric regression setting. We take a different approach, and advocate studying the generalization performance of decision trees with respect to different generative regression models. This allows us to elicit their inductive bias, that is, the assumptions the algorithms make (or do not make) to generalize to new data, thereby guiding practitioners on when and how to apply these methods. In this paper, we focus on sparse additive generative models, which have both low statistical complexity and some nonparametric flexibility. We prove a sharp squared error generalization lower bound for a large class of decision tree algorithms fitted to sparse additive models with $C^1$ component functions. This bound is surprisingly much worse than the minimax rate for estimating such sparse additive models. The inefficiency is due not to greediness, but to the loss in power for detecting global structure when we average responses solely over each leaf, an observation that suggests opportunities to improve tree-based algorithms, for example, by hierarchical shrinkage. To prove these bounds, we develop new technical machinery, establishing a novel connection between decision tree estimation and rate-distortion theory, a sub-field of information theory.