Understanding the Mechanisms of Fast Hyperparameter Transfer

The growing scale of deep learning models has rendered standard hyperparameter (HP) optimization prohibitively expensive. A promising solution is the use of scale-aware hyperparameters, which can enable direct transfer of optimal HPs from small-scale grid searches to large models with minimal performance loss. To understand the principles governing such transfer strategy, we develop a general conceptual framework for reasoning about HP transfer across scale, characterizing transfer as fast when the suboptimality it induces vanishes asymptotically faster than the finite-scale performance gap. We show formally that fast transfer is equivalent to useful transfer for compute-optimal grid search, meaning that transfer is asymptotically more compute-efficient than direct tuning. While empirical work has found that the Maximal Update Parameterization ($μ$P) exhibits fast transfer when scaling model width, the mechanisms remain poorly understood. We show that this property depends critically on problem structure by presenting synthetic settings where transfer either offers provable computational advantage or fails to outperform direct tuning even under $μ$P. To explain the fast transfer observed in practice, we conjecture that decomposing the optimization trajectory reveals two contributions to loss reduction: (1) a width-stable component that determines the optimal HPs, and (2) a width-sensitive component that improves with width but weakly perturbs the HP optimum. We present empirical evidence for this hypothesis across various settings, including large language model pretraining.

GSM-Agent: Understanding Agentic Reasoning Using Controllable Environments

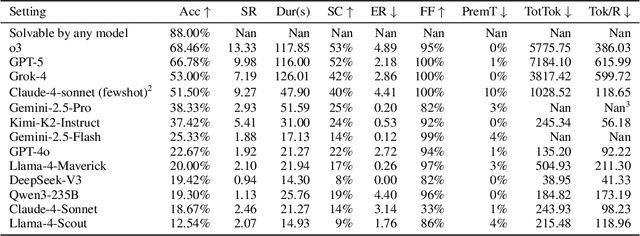
As LLMs are increasingly deployed as agents, agentic reasoning - the ability to combine tool use, especially search, and reasoning - becomes a critical skill. However, it is hard to disentangle agentic reasoning when evaluated in complex environments and tasks. Current agent benchmarks often mix agentic reasoning with challenging math reasoning, expert-level knowledge, and other advanced capabilities. To fill this gap, we build a novel benchmark, GSM-Agent, where an LLM agent is required to solve grade-school-level reasoning problems, but is only presented with the question in the prompt without the premises that contain the necessary information to solve the task, and needs to proactively collect that information using tools. Although the original tasks are grade-school math problems, we observe that even frontier models like GPT-5 only achieve 67% accuracy. To understand and analyze the agentic reasoning patterns, we propose the concept of agentic reasoning graph: cluster the environment's document embeddings into nodes, and map each tool call to its nearest node to build a reasoning path. Surprisingly, we identify that the ability to revisit a previously visited node, widely taken as a crucial pattern in static reasoning, is often missing for agentic reasoning for many models. Based on the insight, we propose a tool-augmented test-time scaling method to improve LLM's agentic reasoning performance by adding tools to encourage models to revisit. We expect our benchmark and the agentic reasoning framework to aid future studies of understanding and pushing the boundaries of agentic reasoning.

PLoP: Precise LoRA Placement for Efficient Finetuning of Large Models

Low-Rank Adaptation (LoRA) is a widely used finetuning method for large models. Its small memory footprint allows practitioners to adapt large models to specific tasks at a fraction of the cost of full finetuning. Different modifications have been proposed to enhance its efficiency by, for example, setting the learning rate, the rank, and the initialization. Another improvement axis is adapter placement strategy: when using LoRA, practitioners usually pick module types to adapt with LoRA, such as Query and Key modules. Few works have studied the problem of adapter placement, with nonconclusive results: original LoRA paper suggested placing adapters in attention modules, while other works suggested placing them in the MLP modules. Through an intuitive theoretical analysis, we introduce PLoP (Precise LoRA Placement), a lightweight method that allows automatic identification of module types where LoRA adapters should be placed, given a pretrained model and a finetuning task. We demonstrate that PLoP consistently outperforms, and in the worst case competes, with commonly used placement strategies through comprehensive experiments on supervised finetuning and reinforcement learning for reasoning.

The Impact of Initialization on LoRA Finetuning Dynamics

In this paper, we study the role of initialization in Low Rank Adaptation (LoRA) as originally introduced in Hu et al. (2021). Essentially, to start from the pretrained model as initialization for finetuning, one can either initialize B to zero and A to random (default initialization in PEFT package), or vice-versa. In both cases, the product BA is equal to zero at initialization, which makes finetuning starts from the pretrained model. These two initialization schemes are seemingly similar. They should in-principle yield the same performance and share the same optimal learning rate. We demonstrate that this is an incorrect intuition and that the first scheme (initializing B to zero and A to random) on average yields better performance compared to the other scheme. Our theoretical analysis shows that the reason behind this might be that the first initialization allows the use of larger learning rates (without causing output instability) compared to the second initialization, resulting in more efficient learning of the first scheme. We validate our results with extensive experiments on LLMs.

LoRA+: Efficient Low Rank Adaptation of Large Models

In this paper, we show that Low Rank Adaptation (LoRA) as originally introduced in Hu et al. (2021) leads to suboptimal finetuning of models with large width (embedding dimension). This is due to the fact that adapter matrices A and B in LoRA are updated with the same learning rate. Using scaling arguments for large width networks, we demonstrate that using the same learning rate for A and B does not allow efficient feature learning. We then show that this suboptimality of LoRA can be corrected simply by setting different learning rates for the LoRA adapter matrices A and B with a well-chosen ratio. We call this proposed algorithm LoRA$+$. In our extensive experiments, LoRA$+$ improves performance (1-2 $\%$ improvements) and finetuning speed (up to $\sim$ 2X SpeedUp), at the same computational cost as LoRA.

More is Better in Modern Machine Learning: when Infinite Overparameterization is Optimal and Overfitting is Obligatory

In our era of enormous neural networks, empirical progress has been driven by the philosophy that more is better. Recent deep learning practice has found repeatedly that larger model size, more data, and more computation (resulting in lower training loss) improves performance. In this paper, we give theoretical backing to these empirical observations by showing that these three properties hold in random feature (RF) regression, a class of models equivalent to shallow networks with only the last layer trained. Concretely, we first show that the test risk of RF regression decreases monotonically with both the number of features and the number of samples, provided the ridge penalty is tuned optimally. In particular, this implies that infinite width RF architectures are preferable to those of any finite width. We then proceed to demonstrate that, for a large class of tasks characterized by powerlaw eigenstructure, training to near-zero training loss is obligatory: near-optimal performance can only be achieved when the training error is much smaller than the test error. Grounding our theory in real-world data, we find empirically that standard computer vision tasks with convolutional neural tangent kernels clearly fall into this class. Taken together, our results tell a simple, testable story of the benefits of overparameterization, overfitting, and more data in random feature models.

The Effect of SGD Batch Size on Autoencoder Learning: Sparsity, Sharpness, and Feature Learning

In this work, we investigate the dynamics of stochastic gradient descent (SGD) when training a single-neuron autoencoder with linear or ReLU activation on orthogonal data. We show that for this non-convex problem, randomly initialized SGD with a constant step size successfully finds a global minimum for any batch size choice. However, the particular global minimum found depends upon the batch size. In the full-batch setting, we show that the solution is dense (i.e., not sparse) and is highly aligned with its initialized direction, showing that relatively little feature learning occurs. On the other hand, for any batch size strictly smaller than the number of samples, SGD finds a global minimum which is sparse and nearly orthogonal to its initialization, showing that the randomness of stochastic gradients induces a qualitatively different type of "feature selection" in this setting. Moreover, if we measure the sharpness of the minimum by the trace of the Hessian, the minima found with full batch gradient descent are flatter than those found with strictly smaller batch sizes, in contrast to previous works which suggest that large batches lead to sharper minima. To prove convergence of SGD with a constant step size, we introduce a powerful tool from the theory of non-homogeneous random walks which may be of independent interest.

The Power of External Memory in Increasing Predictive Model Capacity

One way of introducing sparsity into deep networks is by attaching an external table of parameters that is sparsely looked up at different layers of the network. By storing the bulk of the parameters in the external table, one can increase the capacity of the model without necessarily increasing the inference time. Two crucial questions in this setting are then: what is the lookup function for accessing the table and how are the contents of the table consumed? Prominent methods for accessing the table include 1) using words/wordpieces token-ids as table indices, 2) LSH hashing the token vector in each layer into a table of buckets, and 3) learnable softmax style routing to a table entry. The ways to consume the contents include adding/concatenating to input representation, and using the contents as expert networks that specialize to different inputs. In this work, we conduct rigorous experimental evaluations of existing ideas and their combinations. We also introduce a new method, alternating updates, that enables access to an increased token dimension without increasing the computation time, and demonstrate its effectiveness in language modeling.

Alternating Updates for Efficient Transformers

It is well established that increasing scale in deep transformer networks leads to improved quality and performance. This increase in scale often comes with an increase in compute cost and inference latency. Consequently, research into methods which help realize the benefits of increased scale without leading to an increase in the compute cost becomes important. We introduce Alternating Updates (AltUp), a simple-to-implement method to increase a model's capacity without the computational burden. AltUp enables the widening of the learned representation without increasing the computation time by working on a subblock of the representation at each layer. Our experiments on various transformer models and language tasks demonstrate the consistent effectiveness of alternating updates on a diverse set of benchmarks. Finally, we present extensions of AltUp to the sequence dimension, and demonstrate how AltUp can be synergistically combined with existing approaches, such as Sparse Mixture-of-Experts models, to obtain efficient models with even higher capacity.

A Universal Trade-off Between the Model Size, Test Loss, and Training Loss of Linear Predictors

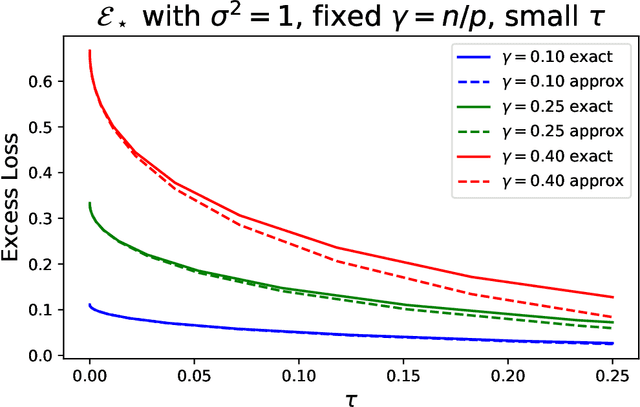
In this work we establish an algorithm and distribution independent non-asymptotic trade-off between the model size, excess test loss, and training loss of linear predictors. Specifically, we show that models that perform well on the test data (have low excess loss) are either "classical" -- have training loss close to the noise level, or are "modern" -- have a much larger number of parameters compared to the minimum needed to fit the training data exactly. We also provide a more precise asymptotic analysis when the limiting spectral distribution of the whitened features is Marchenko-Pastur. Remarkably, while the Marchenko-Pastur analysis is far more precise near the interpolation peak, where the number of parameters is just enough to fit the training data, in settings of most practical interest it differs from the distribution independent bound by only a modest multiplicative constant.