Multi-Armed Bandits with Network Interference

Online experimentation with interference is a common challenge in modern applications such as e-commerce and adaptive clinical trials in medicine. For example, in online marketplaces, the revenue of a good depends on discounts applied to competing goods. Statistical inference with interference is widely studied in the offline setting, but far less is known about how to adaptively assign treatments to minimize regret. We address this gap by studying a multi-armed bandit (MAB) problem where a learner (e-commerce platform) sequentially assigns one of possible $\mathcal{A}$ actions (discounts) to $N$ units (goods) over $T$ rounds to minimize regret (maximize revenue). Unlike traditional MAB problems, the reward of each unit depends on the treatments assigned to other units, i.e., there is interference across the underlying network of units. With $\mathcal{A}$ actions and $N$ units, minimizing regret is combinatorially difficult since the action space grows as $\mathcal{A}^N$. To overcome this issue, we study a sparse network interference model, where the reward of a unit is only affected by the treatments assigned to $s$ neighboring units. We use tools from discrete Fourier analysis to develop a sparse linear representation of the unit-specific reward $r_n: [\mathcal{A}]^N \rightarrow \mathbb{R} $, and propose simple, linear regression-based algorithms to minimize regret. Importantly, our algorithms achieve provably low regret both when the learner observes the interference neighborhood for all units and when it is unknown. This significantly generalizes other works on this topic which impose strict conditions on the strength of interference on a known network, and also compare regret to a markedly weaker optimal action. Empirically, we corroborate our theoretical findings via numerical simulations.

ED-Copilot: Reduce Emergency Department Wait Time with Language Model Diagnostic Assistance

In the emergency department (ED), patients undergo triage and multiple laboratory tests before diagnosis. This process is time-consuming, and causes ED crowding which significantly impacts patient mortality, medical errors, staff burnout, etc. This work proposes (time) cost-effective diagnostic assistance that explores the potential of artificial intelligence (AI) systems in assisting ED clinicians to make time-efficient and accurate diagnoses. Using publicly available patient data, we collaborate with ED clinicians to curate MIMIC-ED-Assist, a benchmark that measures the ability of AI systems in suggesting laboratory tests that minimize ED wait times, while correctly predicting critical outcomes such as death. We develop ED-Copilot which sequentially suggests patient-specific laboratory tests and makes diagnostic predictions. ED-Copilot uses a pre-trained bio-medical language model to encode patient information and reinforcement learning to minimize ED wait time and maximize prediction accuracy of critical outcomes. On MIMIC-ED-Assist, ED-Copilot improves prediction accuracy over baselines while halving average wait time from four hours to two hours. Ablation studies demonstrate the importance of model scale and use of a bio-medical language model. Further analyses reveal the necessity of personalized laboratory test suggestions for diagnosing patients with severe cases, as well as the potential of ED-Copilot in providing ED clinicians with informative laboratory test recommendations. Our code is available at https://github.com/cxcscmu/ED-Copilot.

MDI+: A Flexible Random Forest-Based Feature Importance Framework

Mean decrease in impurity (MDI) is a popular feature importance measure for random forests (RFs). We show that the MDI for a feature $X_k$ in each tree in an RF is equivalent to the unnormalized $R^2$ value in a linear regression of the response on the collection of decision stumps that split on $X_k$. We use this interpretation to propose a flexible feature importance framework called MDI+. Specifically, MDI+ generalizes MDI by allowing the analyst to replace the linear regression model and $R^2$ metric with regularized generalized linear models (GLMs) and metrics better suited for the given data structure. Moreover, MDI+ incorporates additional features to mitigate known biases of decision trees against additive or smooth models. We further provide guidance on how practitioners can choose an appropriate GLM and metric based upon the Predictability, Computability, Stability framework for veridical data science. Extensive data-inspired simulations show that MDI+ significantly outperforms popular feature importance measures in identifying signal features. We also apply MDI+ to two real-world case studies on drug response prediction and breast cancer subtype classification. We show that MDI+ extracts well-established predictive genes with significantly greater stability compared to existing feature importance measures. All code and models are released in a full-fledged python package on Github.

Synthetic Combinations: A Causal Inference Framework for Combinatorial Interventions

We consider a setting with $N$ heterogeneous units and $p$ interventions. Our goal is to learn unit-specific potential outcomes for any combination of these $p$ interventions, i.e., $N \times 2^p$ causal parameters. Choosing combinations of interventions is a problem that naturally arises in many applications such as factorial design experiments, recommendation engines (e.g., showing a set of movies that maximizes engagement for users), combination therapies in medicine, selecting important features for ML models, etc. Running $N \times 2^p$ experiments to estimate the various parameters is infeasible as $N$ and $p$ grow. Further, with observational data there is likely confounding, i.e., whether or not a unit is seen under a combination is correlated with its potential outcome under that combination. To address these challenges, we propose a novel model that imposes latent structure across both units and combinations. We assume latent similarity across units (i.e., the potential outcomes matrix is rank $r$) and regularity in how combinations interact (i.e., the coefficients in the Fourier expansion of the potential outcomes is $s$ sparse). We establish identification for all causal parameters despite unobserved confounding. We propose an estimation procedure, Synthetic Combinations, and establish finite-sample consistency under precise conditions on the observation pattern. Our results imply Synthetic Combinations consistently estimates unit-specific potential outcomes given $\text{poly}(r) \times (N + s^2p)$ observations. In comparison, previous methods that do not exploit structure across both units and combinations have sample complexity scaling as $\min(N \times s^2p, \ \ r \times (N + 2^p))$. We use Synthetic Combinations to propose a data-efficient experimental design mechanism for combinatorial causal inference. We corroborate our theoretical findings with numerical simulations.

Fast Interpretable Greedy-Tree Sums (FIGS)

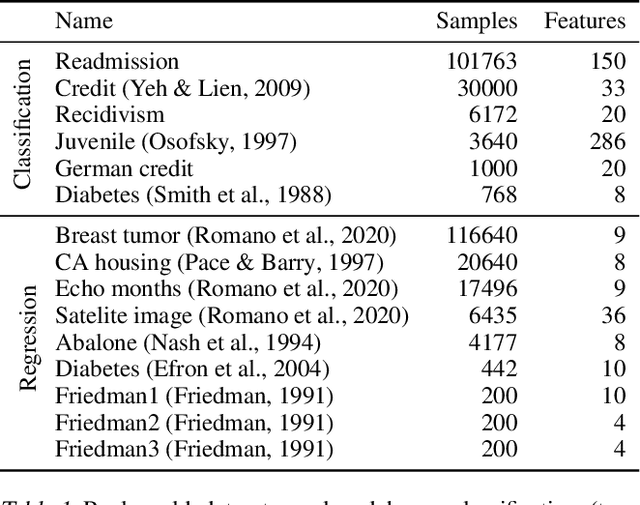
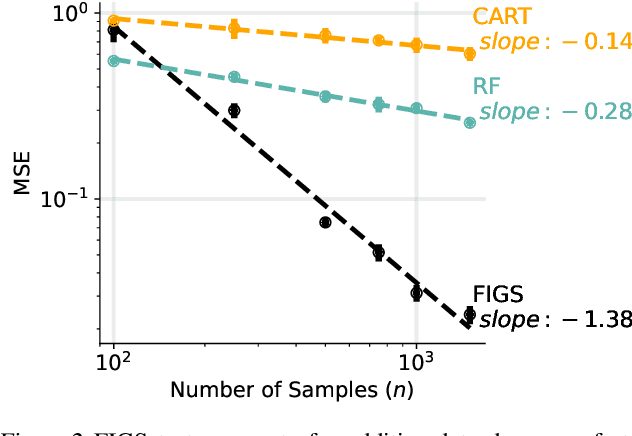
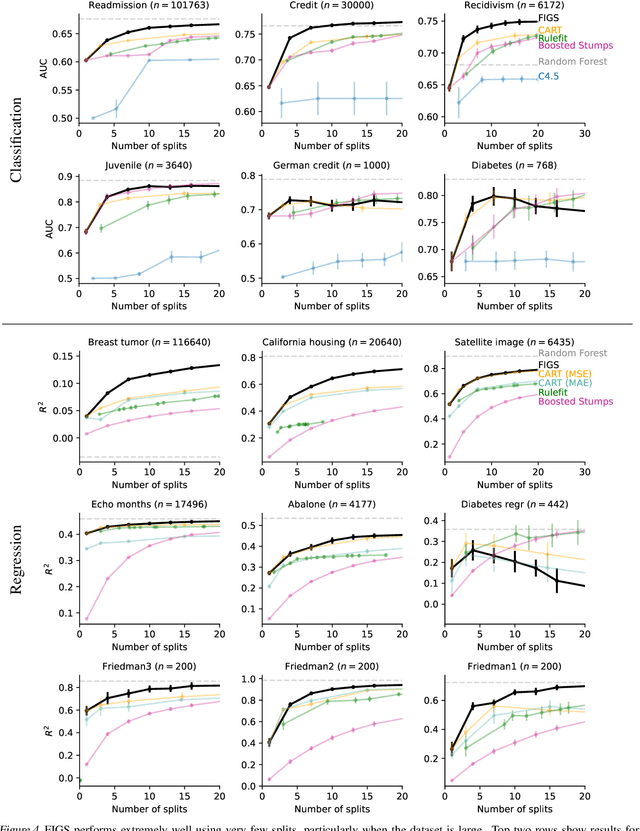
Modern machine learning has achieved impressive prediction performance, but often sacrifices interpretability, a critical consideration in many problems. Here, we propose Fast Interpretable Greedy-Tree Sums (FIGS), an algorithm for fitting concise rule-based models. Specifically, FIGS generalizes the CART algorithm to simultaneously grow a flexible number of trees in a summation. The total number of splits across all the trees can be restricted by a pre-specified threshold, thereby keeping both the size and number of its trees under control. When both are small, the fitted tree-sum can be easily visualized and written out by hand, making it highly interpretable. A partially oracle theoretical result hints at the potential for FIGS to overcome a key weakness of single-tree models by disentangling additive components of generative additive models, thereby reducing redundancy from repeated splits on the same feature. Furthermore, given oracle access to optimal tree structures, we obtain L2 generalization bounds for such generative models in the case of C1 component functions, matching known minimax rates in some cases. Extensive experiments across a wide array of real-world datasets show that FIGS achieves state-of-the-art prediction performance (among all popular rule-based methods) when restricted to just a few splits (e.g. less than 20). We find empirically that FIGS is able to avoid repeated splits, and often provides more concise decision rules than fitted decision trees, without sacrificing predictive performance. All code and models are released in a full-fledged package on Github \url{https://github.com/csinva/imodels}.

Hierarchical Shrinkage: improving the accuracy and interpretability of tree-based methods

Tree-based models such as decision trees and random forests (RF) are a cornerstone of modern machine-learning practice. To mitigate overfitting, trees are typically regularized by a variety of techniques that modify their structure (e.g. pruning). We introduce Hierarchical Shrinkage (HS), a post-hoc algorithm that does not modify the tree structure, and instead regularizes the tree by shrinking the prediction over each node towards the sample means of its ancestors. The amount of shrinkage is controlled by a single regularization parameter and the number of data points in each ancestor. Since HS is a post-hoc method, it is extremely fast, compatible with any tree growing algorithm, and can be used synergistically with other regularization techniques. Extensive experiments over a wide variety of real-world datasets show that HS substantially increases the predictive performance of decision trees, even when used in conjunction with other regularization techniques. Moreover, we find that applying HS to each tree in an RF often improves accuracy, as well as its interpretability by simplifying and stabilizing its decision boundaries and SHAP values. We further explain the success of HS in improving prediction performance by showing its equivalence to ridge regression on a (supervised) basis constructed of decision stumps associated with the internal nodes of a tree. All code and models are released in a full-fledged package available on Github (github.com/csinva/imodels)

A cautionary tale on fitting decision trees to data from additive models: generalization lower bounds

Decision trees are important both as interpretable models amenable to high-stakes decision-making, and as building blocks of ensemble methods such as random forests and gradient boosting. Their statistical properties, however, are not well understood. The most cited prior works have focused on deriving pointwise consistency guarantees for CART in a classical nonparametric regression setting. We take a different approach, and advocate studying the generalization performance of decision trees with respect to different generative regression models. This allows us to elicit their inductive bias, that is, the assumptions the algorithms make (or do not make) to generalize to new data, thereby guiding practitioners on when and how to apply these methods. In this paper, we focus on sparse additive generative models, which have both low statistical complexity and some nonparametric flexibility. We prove a sharp squared error generalization lower bound for a large class of decision tree algorithms fitted to sparse additive models with $C^1$ component functions. This bound is surprisingly much worse than the minimax rate for estimating such sparse additive models. The inefficiency is due not to greediness, but to the loss in power for detecting global structure when we average responses solely over each leaf, an observation that suggests opportunities to improve tree-based algorithms, for example, by hierarchical shrinkage. To prove these bounds, we develop new technical machinery, establishing a novel connection between decision tree estimation and rate-distortion theory, a sub-field of information theory.