Ben Poole
Weakly Supervised Disentanglement with Guarantees
Oct 22, 2019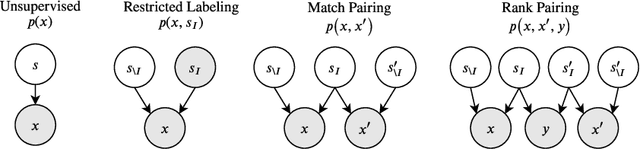

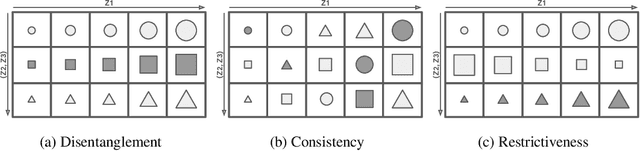

Abstract:Learning disentangled representations that correspond to factors of variation in real-world data is critical to interpretable and human-controllable machine learning. Recently, concerns about the viability of learning disentangled representations in a purely unsupervised manner has spurred a shift toward the incorporation of weak supervision. However, there is currently no formalism that identifies when and how weak supervision will guarantee disentanglement. To address this issue, we provide a theoretical framework to assist in analyzing the disentanglement guarantees (or lack thereof) conferred by weak supervision when coupled with learning algorithms based on distribution matching. We empirically verify the guarantees and limitations of several weak supervision methods (restricted labeling, match-pairing, and rank-pairing), demonstrating the predictive power and usefulness of our theoretical framework.
On Predictive Information Sub-optimality of RNNs
Oct 21, 2019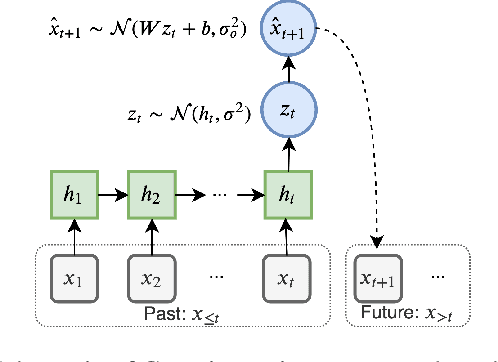
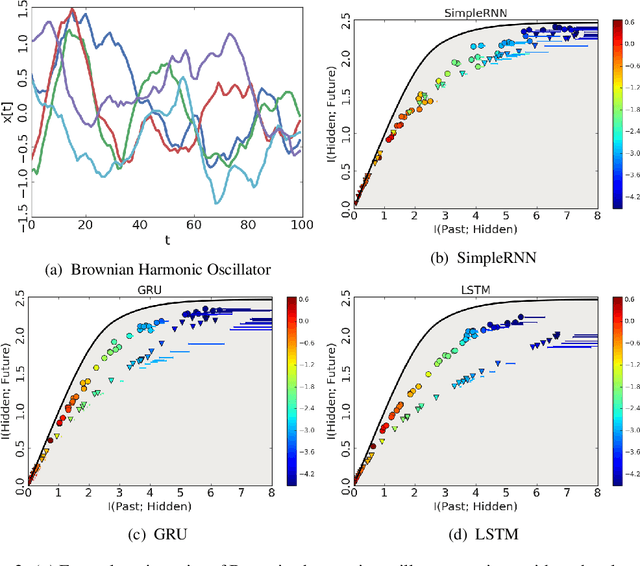
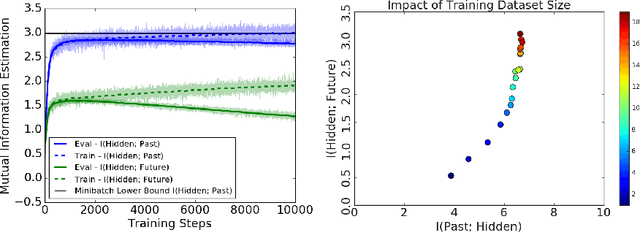
Abstract:Certain biological neurons demonstrate a remarkable capability to optimally compress the history of sensory inputs while being maximally informative about the future. In this work, we investigate if the same can be said of artificial neurons in recurrent neural networks (RNNs) trained with maximum likelihood. In experiments on two datasets, restorative Brownian motion and a hand-drawn sketch dataset, we find that RNNs are sub-optimal in the information plane. Instead of optimally compressing past information, they extract additional information that is not relevant for predicting the future. Overcoming this limitation may require alternative training procedures and architectures, or objectives beyond maximum likelihood estimation.
Improving Robustness Without Sacrificing Accuracy with Patch Gaussian Augmentation
Jun 06, 2019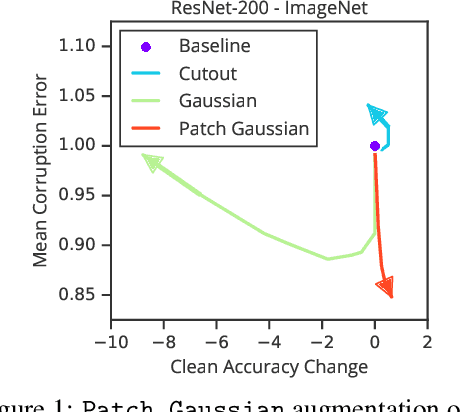
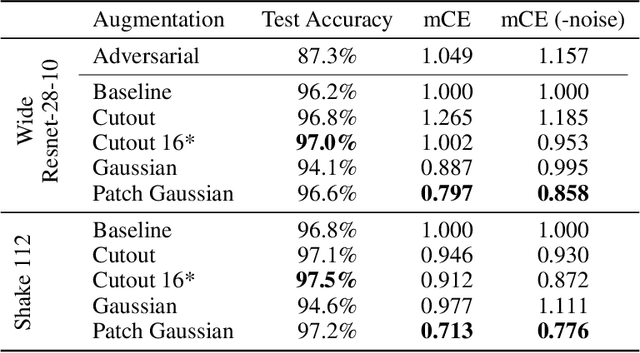
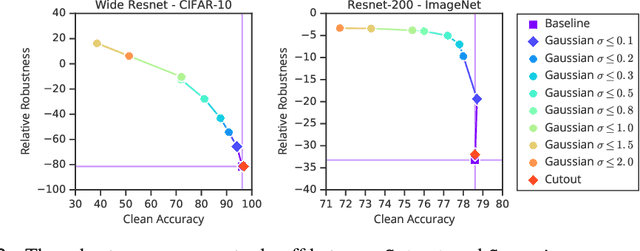
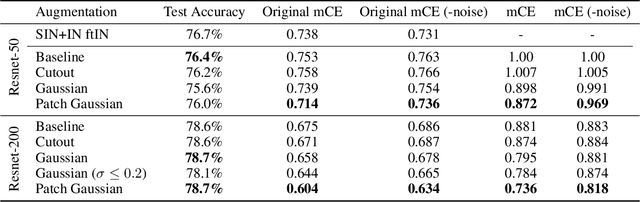
Abstract:Deploying machine learning systems in the real world requires both high accuracy on clean data and robustness to naturally occurring corruptions. While architectural advances have led to improved accuracy, building robust models remains challenging. Prior work has argued that there is an inherent trade-off between robustness and accuracy, which is exemplified by standard data augment techniques such as Cutout, which improves clean accuracy but not robustness, and additive Gaussian noise, which improves robustness but hurts accuracy. To overcome this trade-off, we introduce Patch Gaussian, a simple augmentation scheme that adds noise to randomly selected patches in an input image. Models trained with Patch Gaussian achieve state of the art on the CIFAR-10 and ImageNetCommon Corruptions benchmarks while also improving accuracy on clean data. We find that this augmentation leads to reduced sensitivity to high frequency noise(similar to Gaussian) while retaining the ability to take advantage of relevant high frequency information in the image (similar to Cutout). Finally, we show that Patch Gaussian can be used in conjunction with other regularization methods and data augmentation policies such as AutoAugment, and improves performance on the COCO object detection benchmark.
Discrete Flows: Invertible Generative Models of Discrete Data
May 24, 2019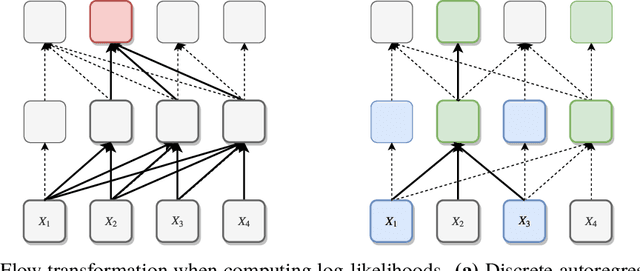

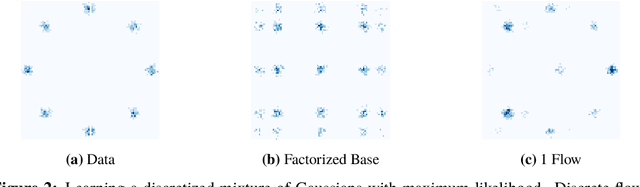
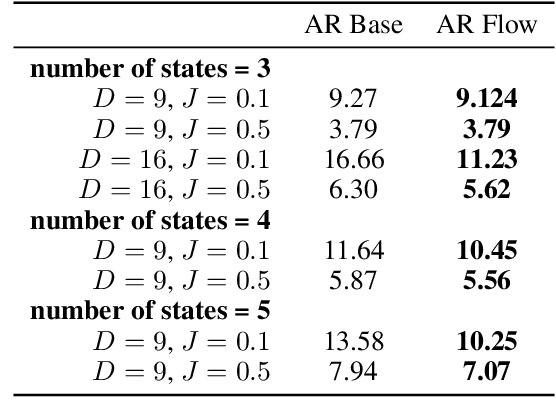
Abstract:While normalizing flows have led to significant advances in modeling high-dimensional continuous distributions, their applicability to discrete distributions remains unknown. In this paper, we show that flows can in fact be extended to discrete events---and under a simple change-of-variables formula not requiring log-determinant-Jacobian computations. Discrete flows have numerous applications. We consider two flow architectures: discrete autoregressive flows that enable bidirectionality, allowing, for example, tokens in text to depend on both left-to-right and right-to-left contexts in an exact language model; and discrete bipartite flows that enable efficient non-autoregressive generation as in RealNVP. Empirically, we find that discrete autoregressive flows outperform autoregressive baselines on synthetic discrete distributions, an addition task, and Potts models; and bipartite flows can obtain competitive performance with autoregressive baselines on character-level language modeling for Penn Tree Bank and text8.
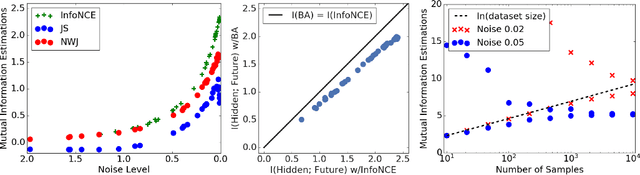
On Variational Bounds of Mutual Information
May 16, 2019



Abstract:Estimating and optimizing Mutual Information (MI) is core to many problems in machine learning; however, bounding MI in high dimensions is challenging. To establish tractable and scalable objectives, recent work has turned to variational bounds parameterized by neural networks, but the relationships and tradeoffs between these bounds remains unclear. In this work, we unify these recent developments in a single framework. We find that the existing variational lower bounds degrade when the MI is large, exhibiting either high bias or high variance. To address this problem, we introduce a continuum of lower bounds that encompasses previous bounds and flexibly trades off bias and variance. On high-dimensional, controlled problems, we empirically characterize the bias and variance of the bounds and their gradients and demonstrate the effectiveness of our new bounds for estimation and representation learning.
Preventing Posterior Collapse with delta-VAEs
Jan 10, 2019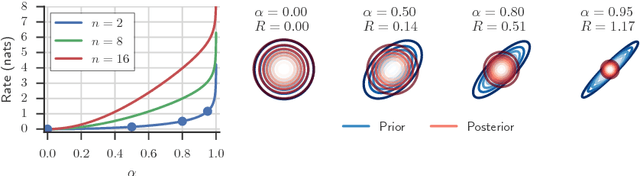
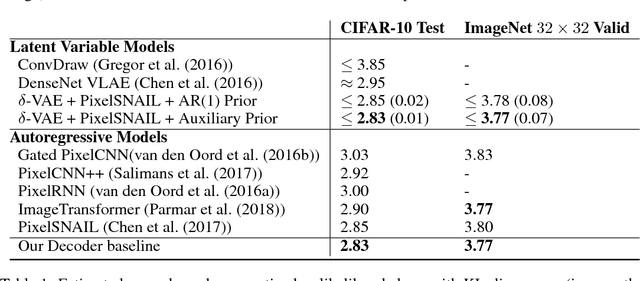
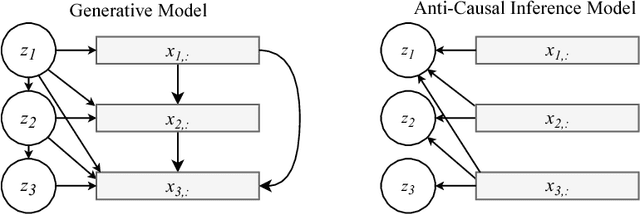

Abstract:Due to the phenomenon of "posterior collapse," current latent variable generative models pose a challenging design choice that either weakens the capacity of the decoder or requires augmenting the objective so it does not only maximize the likelihood of the data. In this paper, we propose an alternative that utilizes the most powerful generative models as decoders, whilst optimising the variational lower bound all while ensuring that the latent variables preserve and encode useful information. Our proposed $\delta$-VAEs achieve this by constraining the variational family for the posterior to have a minimum distance to the prior. For sequential latent variable models, our approach resembles the classic representation learning approach of slow feature analysis. We demonstrate the efficacy of our approach at modeling text on LM1B and modeling images: learning representations, improving sample quality, and achieving state of the art log-likelihood on CIFAR-10 and ImageNet $32\times 32$.
Fixing a Broken ELBO
Feb 13, 2018
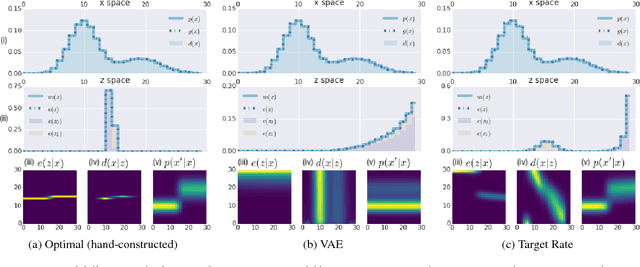
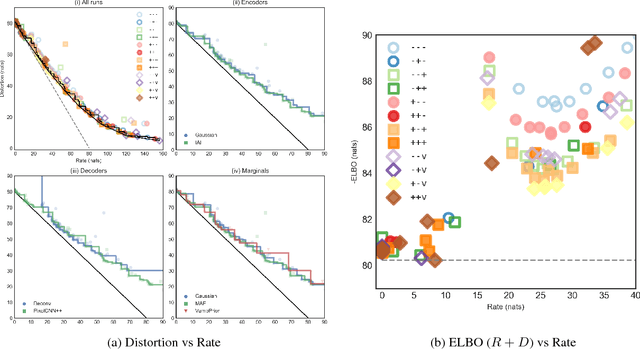
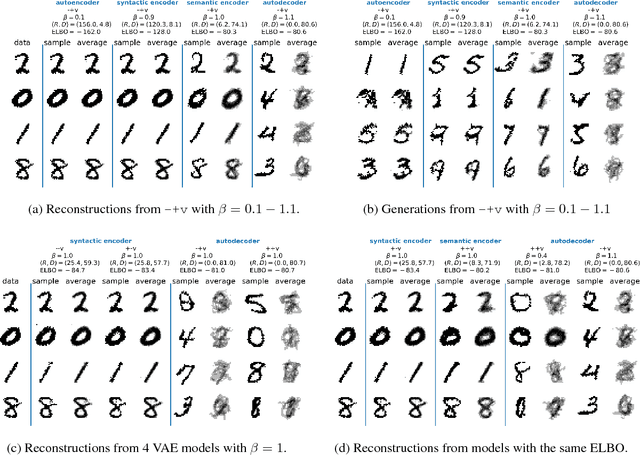
Abstract:Recent work in unsupervised representation learning has focused on learning deep directed latent-variable models. Fitting these models by maximizing the marginal likelihood or evidence is typically intractable, thus a common approximation is to maximize the evidence lower bound (ELBO) instead. However, maximum likelihood training (whether exact or approximate) does not necessarily result in a good latent representation, as we demonstrate both theoretically and empirically. In particular, we derive variational lower and upper bounds on the mutual information between the input and the latent variable, and use these bounds to derive a rate-distortion curve that characterizes the tradeoff between compression and reconstruction accuracy. Using this framework, we demonstrate that there is a family of models with identical ELBO, but different quantitative and qualitative characteristics. Our framework also suggests a simple new method to ensure that latent variable models with powerful stochastic decoders do not ignore their latent code.
Categorical Reparameterization with Gumbel-Softmax
Aug 05, 2017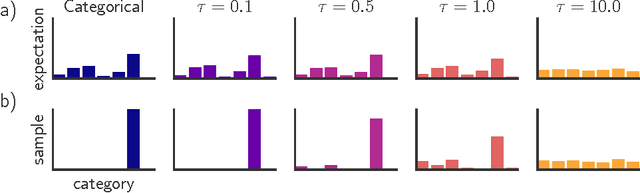

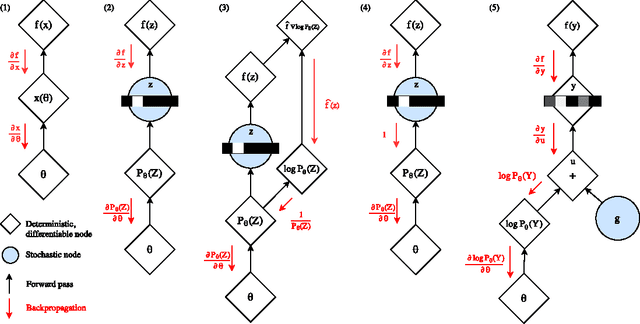
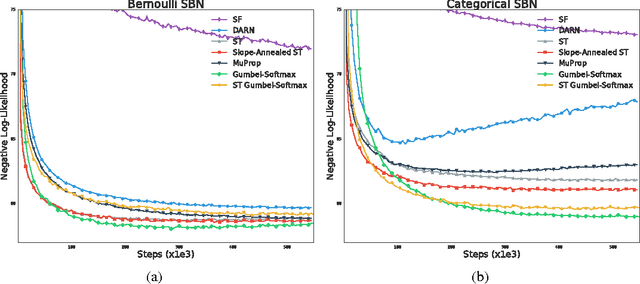
Abstract:Categorical variables are a natural choice for representing discrete structure in the world. However, stochastic neural networks rarely use categorical latent variables due to the inability to backpropagate through samples. In this work, we present an efficient gradient estimator that replaces the non-differentiable sample from a categorical distribution with a differentiable sample from a novel Gumbel-Softmax distribution. This distribution has the essential property that it can be smoothly annealed into a categorical distribution. We show that our Gumbel-Softmax estimator outperforms state-of-the-art gradient estimators on structured output prediction and unsupervised generative modeling tasks with categorical latent variables, and enables large speedups on semi-supervised classification.
On the Expressive Power of Deep Neural Networks
Jun 18, 2017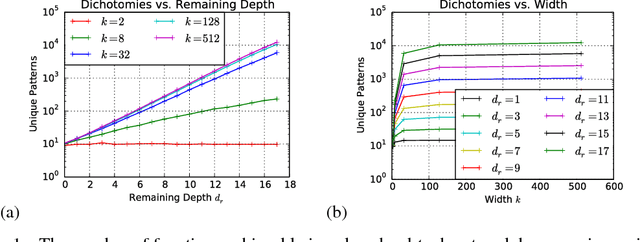


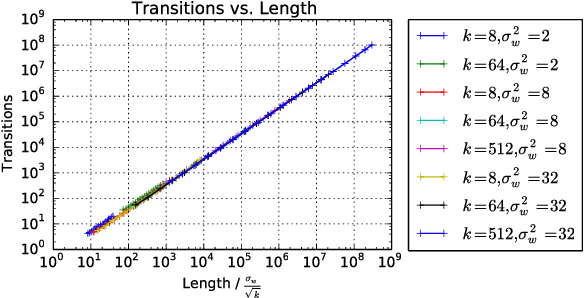
Abstract:We propose a new approach to the problem of neural network expressivity, which seeks to characterize how structural properties of a neural network family affect the functions it is able to compute. Our approach is based on an interrelated set of measures of expressivity, unified by the novel notion of trajectory length, which measures how the output of a network changes as the input sweeps along a one-dimensional path. Our findings can be summarized as follows: (1) The complexity of the computed function grows exponentially with depth. (2) All weights are not equal: trained networks are more sensitive to their lower (initial) layer weights. (3) Regularizing on trajectory length (trajectory regularization) is a simpler alternative to batch normalization, with the same performance.
Continual Learning Through Synaptic Intelligence
Jun 12, 2017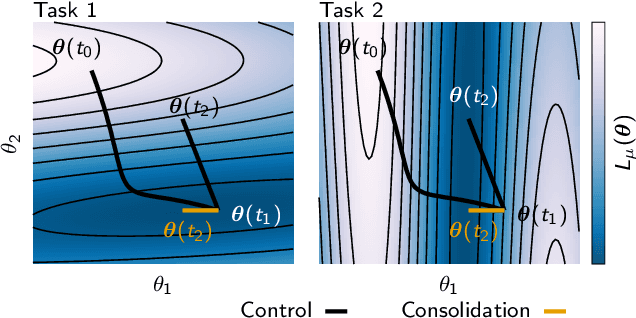
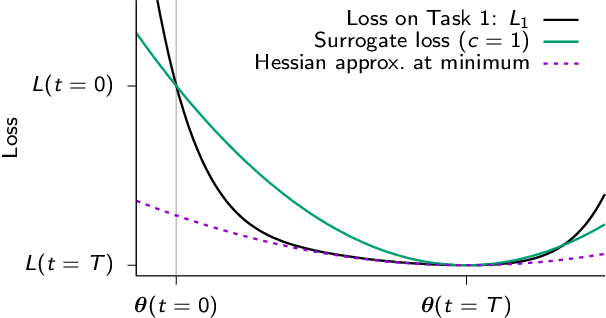
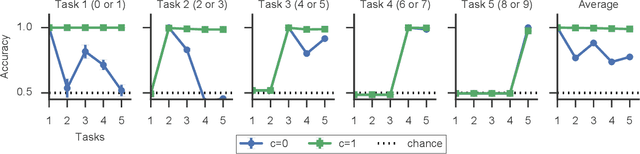
Abstract:While deep learning has led to remarkable advances across diverse applications, it struggles in domains where the data distribution changes over the course of learning. In stark contrast, biological neural networks continually adapt to changing domains, possibly by leveraging complex molecular machinery to solve many tasks simultaneously. In this study, we introduce intelligent synapses that bring some of this biological complexity into artificial neural networks. Each synapse accumulates task relevant information over time, and exploits this information to rapidly store new memories without forgetting old ones. We evaluate our approach on continual learning of classification tasks, and show that it dramatically reduces forgetting while maintaining computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge