David Pfau
A Generalized Bias-Variance Decomposition for Bregman Divergences
Nov 11, 2025Abstract:The bias-variance decomposition is a central result in statistics and machine learning, but is typically presented only for the squared error. We present a generalization of the bias-variance decomposition where the prediction error is a Bregman divergence, which is relevant to maximum likelihood estimation with exponential families. While the result is already known, there was not previously a clear, standalone derivation, so we provide one for pedagogical purposes. A version of this note previously appeared on the author's personal website without context. Here we provide additional discussion and references to the relevant prior literature.
Wasserstein Policy Optimization
May 01, 2025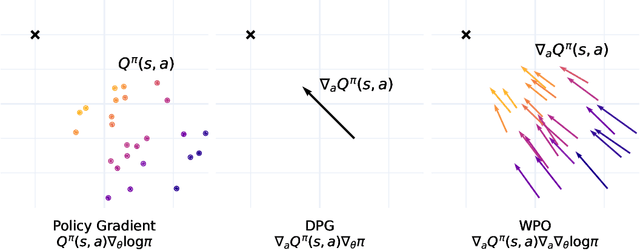
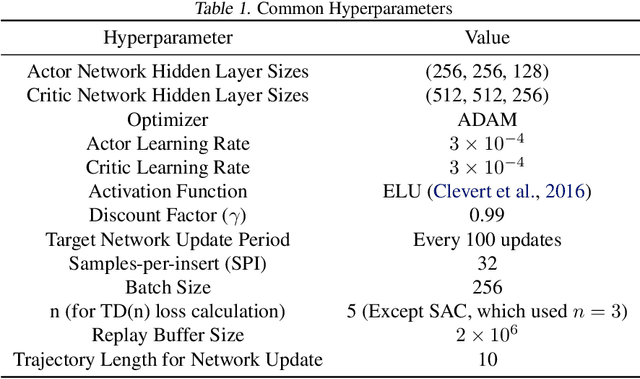
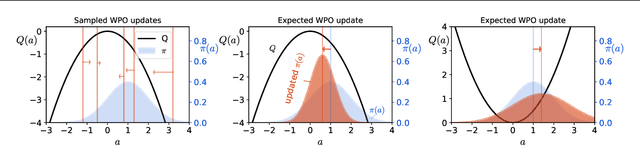
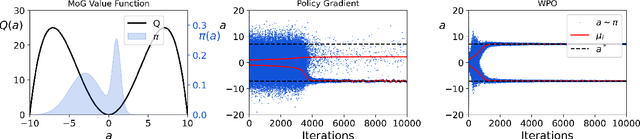
Abstract:We introduce Wasserstein Policy Optimization (WPO), an actor-critic algorithm for reinforcement learning in continuous action spaces. WPO can be derived as an approximation to Wasserstein gradient flow over the space of all policies projected into a finite-dimensional parameter space (e.g., the weights of a neural network), leading to a simple and completely general closed-form update. The resulting algorithm combines many properties of deterministic and classic policy gradient methods. Like deterministic policy gradients, it exploits knowledge of the gradient of the action-value function with respect to the action. Like classic policy gradients, it can be applied to stochastic policies with arbitrary distributions over actions -- without using the reparameterization trick. We show results on the DeepMind Control Suite and a magnetic confinement fusion task which compare favorably with state-of-the-art continuous control methods.
Natural Quantum Monte Carlo Computation of Excited States
Aug 31, 2023Abstract:We present a variational Monte Carlo algorithm for estimating the lowest excited states of a quantum system which is a natural generalization of the estimation of ground states. The method has no free parameters and requires no explicit orthogonalization of the different states, instead transforming the problem of finding excited states of a given system into that of finding the ground state of an expanded system. Expected values of arbitrary observables can be calculated, including off-diagonal expectations between different states such as the transition dipole moment. Although the method is entirely general, it works particularly well in conjunction with recent work on using neural networks as variational Ansatze for many-electron systems, and we show that by combining this method with the FermiNet and Psiformer Ansatze we can accurately recover vertical excitation energies and oscillator strengths on molecules as large as benzene. Beyond the examples on molecules presented here, we expect this technique will be of great interest for applications of variational quantum Monte Carlo to atomic, nuclear and condensed matter physics.
Neural Wave Functions for Superfluids
May 11, 2023



Abstract:Understanding superfluidity remains a major goal of condensed matter physics. Here we tackle this challenge utilizing the recently developed Fermionic neural network (FermiNet) wave function Ansatz for variational Monte Carlo calculations. We study the unitary Fermi gas, a system with strong, short-range, two-body interactions known to possess a superfluid ground state but difficult to describe quantitively. We demonstrate key limitations of the FermiNet Ansatz in studying the unitary Fermi gas and propose a simple modification that outperforms the original FermiNet significantly, giving highly accurate results. We prove mathematically that the new Ansatz is a strict generalization of the original FermiNet architecture, despite the use of fewer parameters. Our approach shares several advantanges with the FermiNet: the use of a neural network removes the need for an underlying basis set; and the flexiblity of the network yields extremely accurate results within a variational quantum Monte Carlo framework that provides access to unbiased estimates of arbitrary ground-state expectation values. We discuss how the method can be extended to study other superfluids.
A Self-Attention Ansatz for Ab-initio Quantum Chemistry
Nov 24, 2022



Abstract:We present a novel neural network architecture using self-attention, the Wavefunction Transformer (Psiformer), which can be used as an approximation (or Ansatz) for solving the many-electron Schr\"odinger equation, the fundamental equation for quantum chemistry and material science. This equation can be solved from first principles, requiring no external training data. In recent years, deep neural networks like the FermiNet and PauliNet have been used to significantly improve the accuracy of these first-principle calculations, but they lack an attention-like mechanism for gating interactions between electrons. Here we show that the Psiformer can be used as a drop-in replacement for these other neural networks, often dramatically improving the accuracy of the calculations. On larger molecules especially, the ground state energy can be improved by dozens of kcal/mol, a qualitative leap over previous methods. This demonstrates that self-attention networks can learn complex quantum mechanical correlations between electrons, and are a promising route to reaching unprecedented accuracy in chemical calculations on larger systems.
Ab-initio quantum chemistry with neural-network wavefunctions
Aug 26, 2022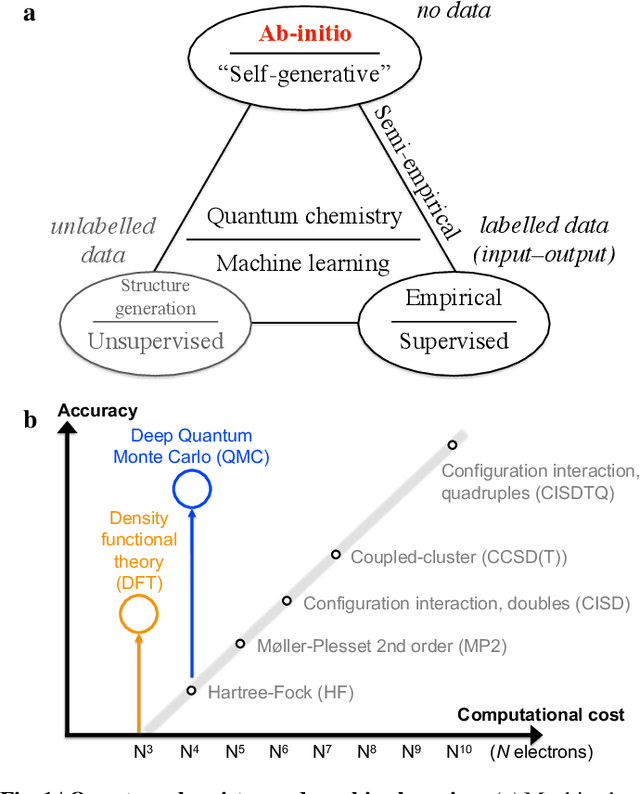
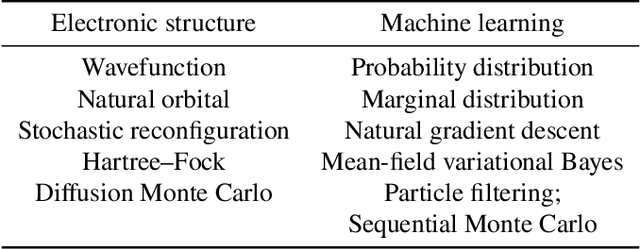
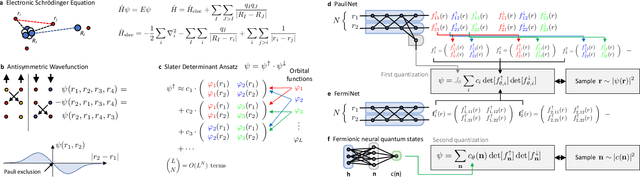
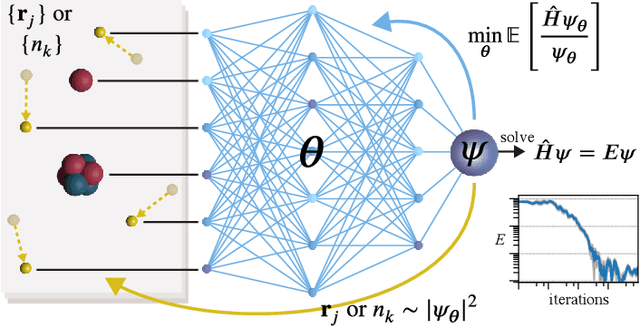
Abstract:Machine learning and specifically deep-learning methods have outperformed human capabilities in many pattern recognition and data processing problems, in game playing, and now also play an increasingly important role in scientific discovery. A key application of machine learning in the molecular sciences is to learn potential energy surfaces or force fields from ab-initio solutions of the electronic Schr\"odinger equation using datasets obtained with density functional theory, coupled cluster, or other quantum chemistry methods. Here we review a recent and complementary approach: using machine learning to aid the direct solution of quantum chemistry problems from first principles. Specifically, we focus on quantum Monte Carlo (QMC) methods that use neural network ansatz functions in order to solve the electronic Schr\"odinger equation, both in first and second quantization, computing ground and excited states, and generalizing over multiple nuclear configurations. Compared to existing quantum chemistry methods, these new deep QMC methods have the potential to generate highly accurate solutions of the Schr\"odinger equation at relatively modest computational cost.
Integrable Nonparametric Flows
Dec 03, 2020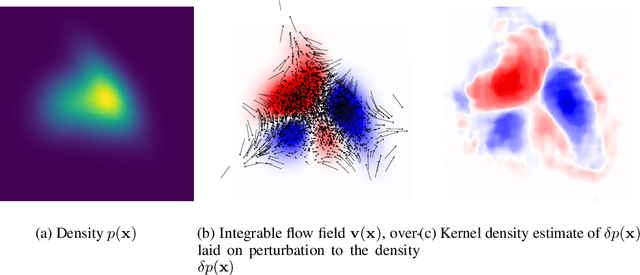
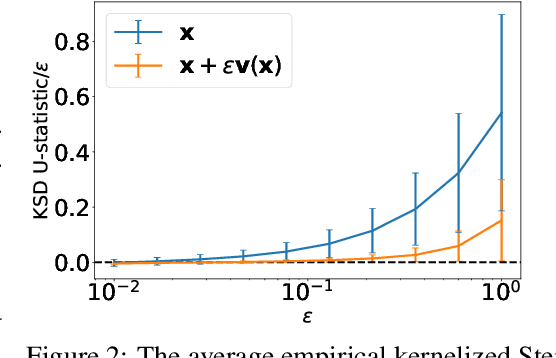
Abstract:We introduce a method for reconstructing an infinitesimal normalizing flow given only an infinitesimal change to a (possibly unnormalized) probability distribution. This reverses the conventional task of normalizing flows -- rather than being given samples from a unknown target distribution and learning a flow that approximates the distribution, we are given a perturbation to an initial distribution and aim to reconstruct a flow that would generate samples from the known perturbed distribution. While this is an underdetermined problem, we find that choosing the flow to be an integrable vector field yields a solution closely related to electrostatics, and a solution can be computed by the method of Green's functions. Unlike conventional normalizing flows, this flow can be represented in an entirely nonparametric manner. We validate this derivation on low-dimensional problems, and discuss potential applications to problems in quantum Monte Carlo and machine learning.
Better, Faster Fermionic Neural Networks
Nov 13, 2020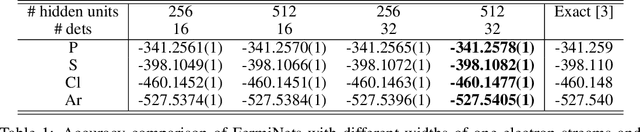
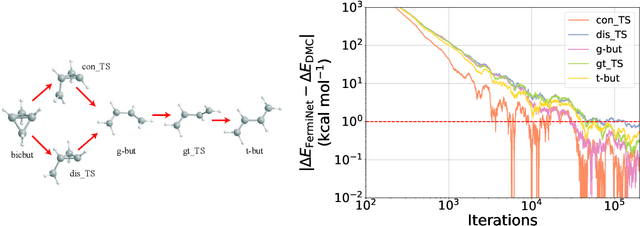

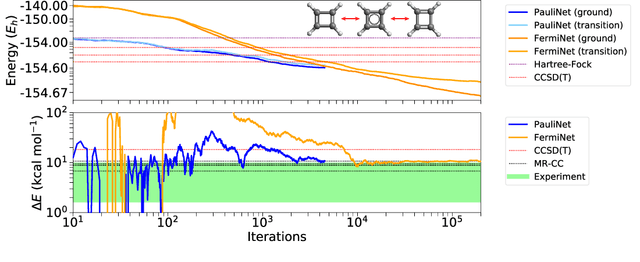
Abstract:The Fermionic Neural Network (FermiNet) is a recently-developed neural network architecture that can be used as a wavefunction Ansatz for many-electron systems, and has already demonstrated high accuracy on small systems. Here we present several improvements to the FermiNet that allow us to set new records for speed and accuracy on challenging systems. We find that increasing the size of the network is sufficient to reach chemical accuracy on atoms as large as argon. Through a combination of implementing FermiNet in JAX and simplifying several parts of the network, we are able to reduce the number of GPU hours needed to train the FermiNet on large systems by an order of magnitude. This enables us to run the FermiNet on the challenging transition of bicyclobutane to butadiene and compare against the PauliNet on the automerization of cyclobutadiene, and we achieve results near the state of the art for both.
Disentangling by Subspace Diffusion
Jun 23, 2020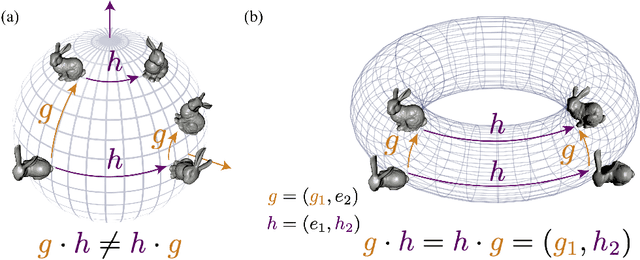

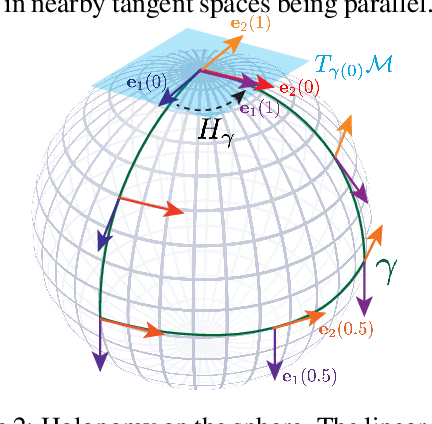
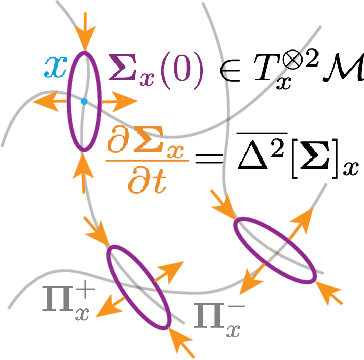
Abstract:We present a novel nonparametric algorithm for symmetry-based disentangling of data manifolds, the Geometric Manifold Component Estimator (GEOMANCER). GEOMANCER provides a partial answer to the question posed by Higgins et al. (2018): is it possible to learn how to factorize a Lie group solely from observations of the orbit of an object it acts on? We show that fully unsupervised factorization of a data manifold is possible *if* the true metric of the manifold is known and each factor manifold has nontrivial holonomy -- for example, rotation in 3D. Our algorithm works by estimating the subspaces that are invariant under random walk diffusion, giving an approximation to the de Rham decomposition from differential geometry. We demonstrate the efficacy of GEOMANCER on several complex synthetic manifolds. Our work reduces the question of whether unsupervised disentangling is possible to the question of whether unsupervised metric learning is possible, providing a unifying insight into the geometric nature of representation learning.
Ab-Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks
Sep 05, 2019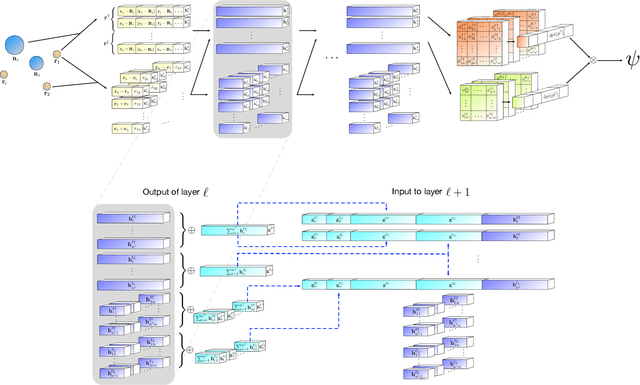
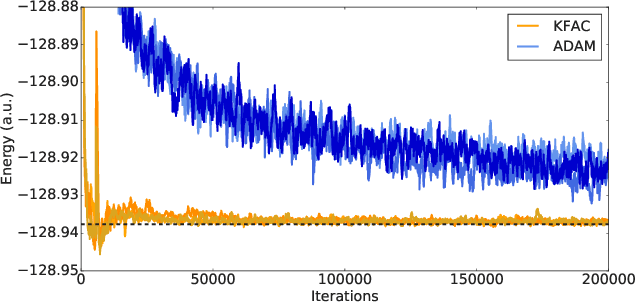
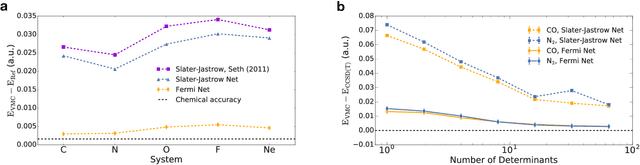
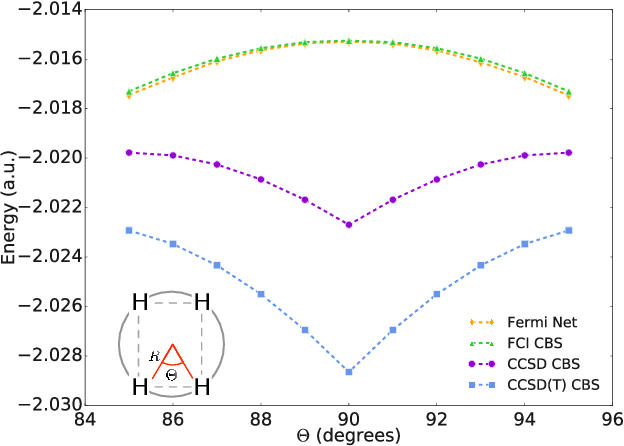
Abstract:Given access to accurate solutions of the many-electron Schr\"odinger equation, nearly all chemistry could be derived from first principles. Exact wavefunctions of interesting chemical systems are out of reach because they are NP-hard to compute in general, but approximations can be found using polynomially-scaling algorithms. The key challenge for many of these algorithms is the choice of wavefunction approximation, or Ansatz, which must trade off between efficiency and accuracy. Neural networks have shown impressive power as accurate practical function approximators and promise as a compact wavefunction Ansatz for spin systems, but problems in electronic structure require wavefunctions that obey Fermi-Dirac statistics. Here we introduce a novel deep learning architecture, the Fermionic Neural Network, as a powerful wavefunction Ansatz for many-electron systems. The Fermionic Neural Network is able to achieve accuracy beyond other variational Monte Carlo Ans\"atze on a variety of atoms and small molecules. Using no data other than atomic positions and charges, we predict the dissociation curves of the nitrogen molecule and hydrogen chain, two challenging strongly-correlated systems, to significantly higher accuracy than the coupled cluster method, widely considered the gold standard for quantum chemistry. This demonstrates that deep neural networks can outperform existing ab-initio quantum chemistry methods, opening the possibility of accurate direct optimisation of wavefunctions for previously intractable molecules and solids.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge