An analytic theory of creativity in convolutional diffusion models

We obtain the first analytic, interpretable and predictive theory of creativity in convolutional diffusion models. Indeed, score-based diffusion models can generate highly creative images that lie far from their training data. But optimal score-matching theory suggests that these models should only be able to produce memorized training examples. To reconcile this theory-experiment gap, we identify two simple inductive biases, locality and equivariance, that: (1) induce a form of combinatorial creativity by preventing optimal score-matching; (2) result in a fully analytic, completely mechanistically interpretable, equivariant local score (ELS) machine that, (3) without any training can quantitatively predict the outputs of trained convolution only diffusion models (like ResNets and UNets) with high accuracy (median $r^2$ of $0.90, 0.91, 0.94$ on CIFAR10, FashionMNIST, and MNIST). Our ELS machine reveals a locally consistent patch mosaic model of creativity, in which diffusion models create exponentially many novel images by mixing and matching different local training set patches in different image locations. Our theory also partially predicts the outputs of pre-trained self-attention enabled UNets (median $r^2 \sim 0.75$ on CIFAR10), revealing an intriguing role for attention in carving out semantic coherence from local patch mosaics.

Fooling LLM graders into giving better grades through neural activity guided adversarial prompting

The deployment of artificial intelligence (AI) in critical decision-making and evaluation processes raises concerns about inherent biases that malicious actors could exploit to distort decision outcomes. We propose a systematic method to reveal such biases in AI evaluation systems and apply it to automated essay grading as an example. Our approach first identifies hidden neural activity patterns that predict distorted decision outcomes and then optimizes an adversarial input suffix to amplify such patterns. We demonstrate that this combination can effectively fool large language model (LLM) graders into assigning much higher grades than humans would. We further show that this white-box attack transfers to black-box attacks on other models, including commercial closed-source models like Gemini. They further reveal the existence of a "magic word" that plays a pivotal role in the efficacy of the attack. We trace the origin of this magic word bias to the structure of commonly-used chat templates for supervised fine-tuning of LLMs and show that a minor change in the template can drastically reduce the bias. This work not only uncovers vulnerabilities in current LLMs but also proposes a systematic method to identify and remove hidden biases, contributing to the goal of ensuring AI safety and security.

Features are fate: a theory of transfer learning in high-dimensional regression

With the emergence of large-scale pre-trained neural networks, methods to adapt such "foundation" models to data-limited downstream tasks have become a necessity. Fine-tuning, preference optimization, and transfer learning have all been successfully employed for these purposes when the target task closely resembles the source task, but a precise theoretical understanding of "task similarity" is still lacking. While conventional wisdom suggests that simple measures of similarity between source and target distributions, such as $\phi$-divergences or integral probability metrics, can directly predict the success of transfer, we prove the surprising fact that, in general, this is not the case. We adopt, instead, a feature-centric viewpoint on transfer learning and establish a number of theoretical results that demonstrate that when the target task is well represented by the feature space of the pre-trained model, transfer learning outperforms training from scratch. We study deep linear networks as a minimal model of transfer learning in which we can analytically characterize the transferability phase diagram as a function of the target dataset size and the feature space overlap. For this model, we establish rigorously that when the feature space overlap between the source and target tasks is sufficiently strong, both linear transfer and fine-tuning improve performance, especially in the low data limit. These results build on an emerging understanding of feature learning dynamics in deep linear networks, and we demonstrate numerically that the rigorous results we derive for the linear case also apply to nonlinear networks.

Get rich quick: exact solutions reveal how unbalanced initializations promote rapid feature learning

While the impressive performance of modern neural networks is often attributed to their capacity to efficiently extract task-relevant features from data, the mechanisms underlying this rich feature learning regime remain elusive, with much of our theoretical understanding stemming from the opposing lazy regime. In this work, we derive exact solutions to a minimal model that transitions between lazy and rich learning, precisely elucidating how unbalanced layer-specific initialization variances and learning rates determine the degree of feature learning. Our analysis reveals that they conspire to influence the learning regime through a set of conserved quantities that constrain and modify the geometry of learning trajectories in parameter and function space. We extend our analysis to more complex linear models with multiple neurons, outputs, and layers and to shallow nonlinear networks with piecewise linear activation functions. In linear networks, rapid feature learning only occurs with balanced initializations, where all layers learn at similar speeds. While in nonlinear networks, unbalanced initializations that promote faster learning in earlier layers can accelerate rich learning. Through a series of experiments, we provide evidence that this unbalanced rich regime drives feature learning in deep finite-width networks, promotes interpretability of early layers in CNNs, reduces the sample complexity of learning hierarchical data, and decreases the time to grokking in modular arithmetic. Our theory motivates further exploration of unbalanced initializations to enhance efficient feature learning.

Geometric Dynamics of Signal Propagation Predict Trainability of Transformers

We investigate forward signal propagation and gradient back propagation in deep, randomly initialized transformers, yielding simple necessary and sufficient conditions on initialization hyperparameters that ensure trainability of deep transformers. Our approach treats the evolution of the representations of $n$ tokens as they propagate through the transformer layers in terms of a discrete time dynamical system of $n$ interacting particles. We derive simple update equations for the evolving geometry of this particle system, starting from a permutation symmetric simplex. Our update equations show that without MLP layers, this system will collapse to a line, consistent with prior work on rank collapse in transformers. However, unlike prior work, our evolution equations can quantitatively track particle geometry in the additional presence of nonlinear MLP layers, and it reveals an order-chaos phase transition as a function of initialization hyperparameters, like the strength of attentional and MLP residual connections and weight variances. In the ordered phase the particles are attractive and collapse to a line, while in the chaotic phase the particles are repulsive and converge to a regular $n$-simplex. We analytically derive two Lyapunov exponents: an angle exponent that governs departures from the edge of chaos in this particle system, and a gradient exponent that governs the rate of exponential growth or decay of backpropagated gradients. We show through experiments that, remarkably, the final test loss at the end of training is well predicted just by these two exponents at the beginning of training, and that the simultaneous vanishing of these two exponents yields a simple necessary and sufficient condition to achieve minimal test loss.

Pretraining task diversity and the emergence of non-Bayesian in-context learning for regression

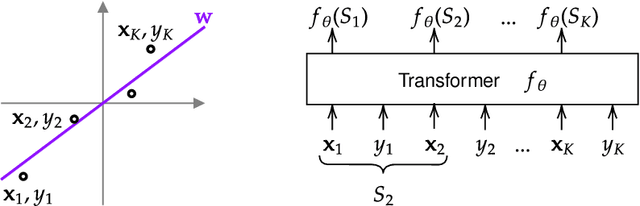
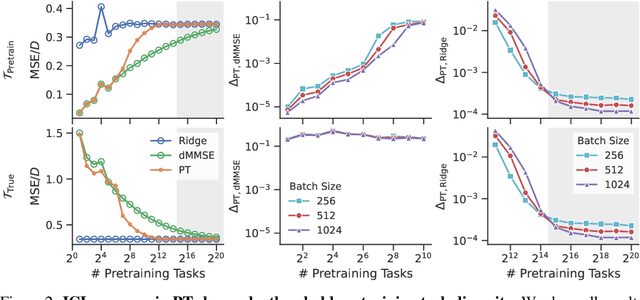
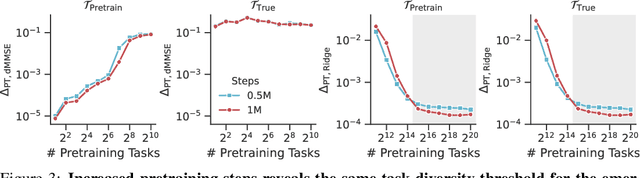
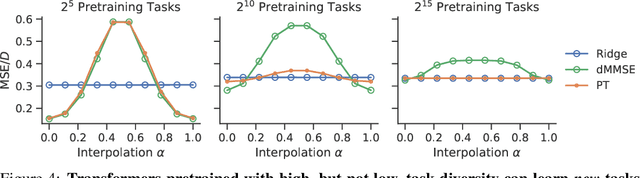
Pretrained transformers exhibit the remarkable ability of in-context learning (ICL): they can learn tasks from just a few examples provided in the prompt without updating any weights. This raises a foundational question: can ICL solve fundamentally $\textit{new}$ tasks that are very different from those seen during pretraining? To probe this question, we examine ICL's performance on linear regression while varying the diversity of tasks in the pretraining dataset. We empirically demonstrate a $\textit{task diversity threshold}$ for the emergence of ICL. Below this threshold, the pretrained transformer cannot solve unseen regression tasks as it behaves like a Bayesian estimator with the $\textit{non-diverse pretraining task distribution}$ as the prior. Beyond this threshold, the transformer significantly outperforms this estimator; its behavior aligns with that of ridge regression, corresponding to a Gaussian prior over $\textit{all tasks}$, including those not seen during pretraining. These results highlight that, when pretrained on data with task diversity greater than the threshold, transformers $\textit{can}$ solve fundamentally new tasks in-context. Importantly, this capability hinges on it deviating from the Bayes optimal estimator with the pretraining distribution as the prior. This study underscores, in a concrete example, the critical role of task diversity, alongside data and model scale, in the emergence of ICL. Code is available at https://github.com/mansheej/icl-task-diversity.

Stochastic Collapse: How Gradient Noise Attracts SGD Dynamics Towards Simpler Subnetworks

In this work, we reveal a strong implicit bias of stochastic gradient descent (SGD) that drives overly expressive networks to much simpler subnetworks, thereby dramatically reducing the number of independent parameters, and improving generalization. To reveal this bias, we identify invariant sets, or subsets of parameter space that remain unmodified by SGD. We focus on two classes of invariant sets that correspond to simpler subnetworks and commonly appear in modern architectures. Our analysis uncovers that SGD exhibits a property of stochastic attractivity towards these simpler invariant sets. We establish a sufficient condition for stochastic attractivity based on a competition between the loss landscape's curvature around the invariant set and the noise introduced by stochastic gradients. Remarkably, we find that an increased level of noise strengthens attractivity, leading to the emergence of attractive invariant sets associated with saddle-points or local maxima of the train loss. We observe empirically the existence of attractive invariant sets in trained deep neural networks, implying that SGD dynamics often collapses to simple subnetworks with either vanishing or redundant neurons. We further demonstrate how this simplifying process of stochastic collapse benefits generalization in a linear teacher-student framework. Finally, through this analysis, we mechanistically explain why early training with large learning rates for extended periods benefits subsequent generalization.

SemDeDup: Data-efficient learning at web-scale through semantic deduplication

Progress in machine learning has been driven in large part by massive increases in data. However, large web-scale datasets such as LAION are largely uncurated beyond searches for exact duplicates, potentially leaving much redundancy. Here, we introduce SemDeDup, a method which leverages embeddings from pre-trained models to identify and remove semantic duplicates: data pairs which are semantically similar, but not exactly identical. Removing semantic duplicates preserves performance and speeds up learning. Analyzing a subset of LAION, we show that SemDeDup can remove 50% of the data with minimal performance loss, effectively halving training time. Moreover, performance increases out of distribution. Also, analyzing language models trained on C4, a partially curated dataset, we show that SemDeDup improves over prior approaches while providing efficiency gains. SemDeDup provides an example of how simple ways of leveraging quality embeddings can be used to make models learn faster with less data.

Holistic Evaluation of Language Models

Language models (LMs) are becoming the foundation for almost all major language technologies, but their capabilities, limitations, and risks are not well understood. We present Holistic Evaluation of Language Models (HELM) to improve the transparency of language models. First, we taxonomize the vast space of potential scenarios (i.e. use cases) and metrics (i.e. desiderata) that are of interest for LMs. Then we select a broad subset based on coverage and feasibility, noting what's missing or underrepresented (e.g. question answering for neglected English dialects, metrics for trustworthiness). Second, we adopt a multi-metric approach: We measure 7 metrics (accuracy, calibration, robustness, fairness, bias, toxicity, and efficiency) for each of 16 core scenarios when possible (87.5% of the time). This ensures metrics beyond accuracy don't fall to the wayside, and that trade-offs are clearly exposed. We also perform 7 targeted evaluations, based on 26 targeted scenarios, to analyze specific aspects (e.g. reasoning, disinformation). Third, we conduct a large-scale evaluation of 30 prominent language models (spanning open, limited-access, and closed models) on all 42 scenarios, 21 of which were not previously used in mainstream LM evaluation. Prior to HELM, models on average were evaluated on just 17.9% of the core HELM scenarios, with some prominent models not sharing a single scenario in common. We improve this to 96.0%: now all 30 models have been densely benchmarked on the same core scenarios and metrics under standardized conditions. Our evaluation surfaces 25 top-level findings. For full transparency, we release all raw model prompts and completions publicly for further analysis, as well as a general modular toolkit. We intend for HELM to be a living benchmark for the community, continuously updated with new scenarios, metrics, and models.

Toward Next-Generation Artificial Intelligence: Catalyzing the NeuroAI Revolution

Neuroscience has long been an important driver of progress in artificial intelligence (AI). We propose that to accelerate progress in AI, we must invest in fundamental research in NeuroAI.