A New Decomposition Paradigm for Graph-structured Nonlinear Programs via Message Passing

We study finite-sum nonlinear programs whose decision variables interact locally according to a graph or hypergraph. We propose MP-Jacobi (Message Passing-Jacobi), a graph-compliant decentralized framework that couples min-sum message passing with Jacobi block updates. The (hyper)graph is partitioned into tree clusters. At each iteration, agents update in parallel by solving a cluster subproblem whose objective decomposes into (i) an intra-cluster term evaluated by a single min-sum sweep on the cluster tree (cost-to-go messages) and (ii) inter-cluster couplings handled via a Jacobi correction using neighbors' latest iterates. This design uses only single-hop communication and yields a convergent message-passing method on loopy graphs. For strongly convex objectives we establish global linear convergence and explicit rates that quantify how curvature, coupling strength, and the chosen partition affect scalability and provide guidance for clustering. To mitigate the computation and communication cost of exact message updates, we develop graph-compliant surrogates that preserve convergence while reducing per-iteration complexity. We further extend MP-Jacobi to hypergraphs; in heavily overlapping regimes, a surrogate-based hyperedge-splitting scheme restores finite-time intra-cluster message updates and maintains convergence. Experiments validate the theory and show consistent improvements over decentralized gradient baselines.

A Multi-Level Framework for Multi-Objective Hypergraph Partitioning: Combining Minimum Spanning Tree and Proximal Gradient

This paper proposes an efficient hypergraph partitioning framework based on a novel multi-objective non-convex constrained relaxation model. A modified accelerated proximal gradient algorithm is employed to generate diverse $k$-dimensional vertex features to avoid local optima and enhance partition quality. Two MST-based strategies are designed for different data scales: for small-scale data, the Prim algorithm constructs a minimum spanning tree followed by pruning and clustering; for large-scale data, a subset of representative nodes is selected to build a smaller MST, while the remaining nodes are assigned accordingly to reduce complexity. To further improve partitioning results, refinement strategies including greedy migration, swapping, and recursive MST-based clustering are introduced for partitions. Experimental results on public benchmark sets demonstrate that the proposed algorithm achieves reductions in cut size of approximately 2\%--5\% on average compared to KaHyPar in 2, 3, and 4-way partitioning, with improvements of up to 35\% on specific instances. Particularly on weighted vertex sets, our algorithm outperforms state-of-the-art partitioners including KaHyPar, hMetis, Mt-KaHyPar, and K-SpecPart, highlighting its superior partitioning quality and competitiveness. Furthermore, the proposed refinement strategy improves hMetis partitions by up to 16\%. A comprehensive evaluation based on virtual instance methodology and parameter sensitivity analysis validates the algorithm's competitiveness and characterizes its performance trade-offs.

Deep k-grouping: An Unsupervised Learning Framework for Combinatorial Optimization on Graphs and Hypergraphs

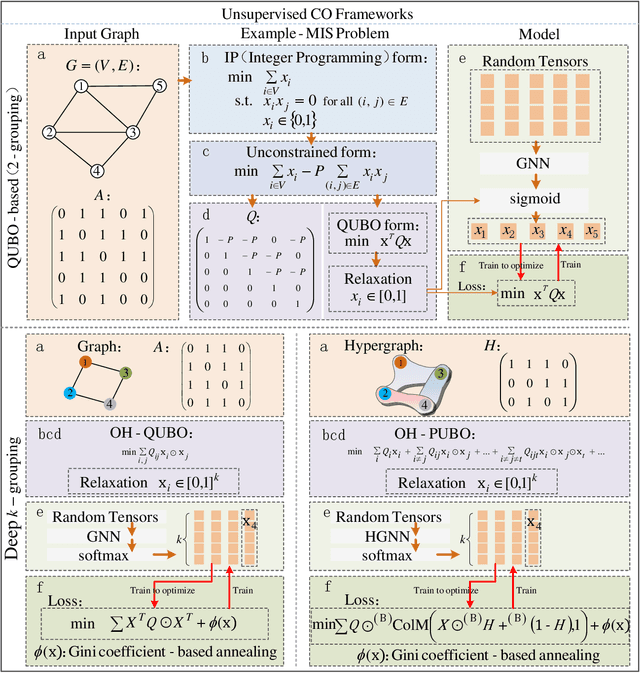
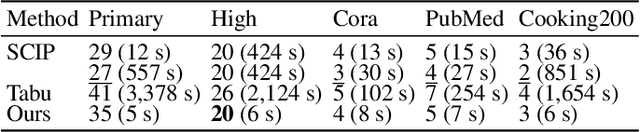
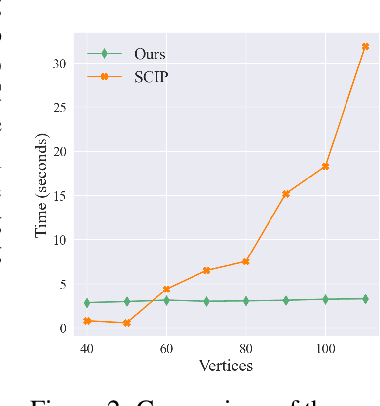
Along with AI computing shining in scientific discovery, its potential in the combinatorial optimization (CO) domain has also emerged in recent years. Yet, existing unsupervised neural network solvers struggle to solve $k$-grouping problems (e.g., coloring, partitioning) on large-scale graphs and hypergraphs, due to limited computational frameworks. In this work, we propose Deep $k$-grouping, an unsupervised learning-based CO framework. Specifically, we contribute: Novel one-hot encoded polynomial unconstrained binary optimization (OH-PUBO), a formulation for modeling k-grouping problems on graphs and hypergraphs (e.g., graph/hypergraph coloring and partitioning); GPU-accelerated algorithms for large-scale k-grouping CO problems. Deep $k$-grouping employs the relaxation of large-scale OH-PUBO objectives as differentiable loss functions and trains to optimize them in an unsupervised manner. To ensure scalability, it leverages GPU-accelerated algorithms to unify the training pipeline; A Gini coefficient-based continuous relaxation annealing strategy to enforce discreteness of solutions while preventing convergence to local optima. Experimental results demonstrate that Deep $k$-grouping outperforms existing neural network solvers and classical heuristics such as SCIP and Tabu.

A packing lemma for VCN${}_k$-dimension and learning high-dimensional data

Recently, the authors introduced the theory of high-arity PAC learning, which is well-suited for learning graphs, hypergraphs and relational structures. In the same initial work, the authors proved a high-arity analogue of the Fundamental Theorem of Statistical Learning that almost completely characterizes all notions of high-arity PAC learning in terms of a combinatorial dimension, called the Vapnik--Chervonenkis--Natarajan (VCN${}_k$) $k$-dimension, leaving as an open problem only the characterization of non-partite, non-agnostic high-arity PAC learnability. In this work, we complete this characterization by proving that non-partite non-agnostic high-arity PAC learnability implies a high-arity version of the Haussler packing property, which in turn implies finiteness of VCN${}_k$-dimension. This is done by obtaining direct proofs that classic PAC learnability implies classic Haussler packing property, which in turn implies finite Natarajan dimension and noticing that these direct proofs nicely lift to high-arity.

Overlap-aware meta-learning attention to enhance hypergraph neural networks for node classification

Although hypergraph neural networks (HGNNs) have emerged as a powerful framework for analyzing complex datasets, their practical performance often remains limited. On one hand, existing networks typically employ a single type of attention mechanism, focusing on either structural or feature similarities during message passing. On the other hand, assuming that all nodes in current hypergraph models have the same level of overlap may lead to suboptimal generalization. To overcome these limitations, we propose a novel framework, overlap-aware meta-learning attention for hypergraph neural networks (OMA-HGNN). First, we introduce a hypergraph attention mechanism that integrates both structural and feature similarities. Specifically, we linearly combine their respective losses with weighted factors for the HGNN model. Second, we partition nodes into different tasks based on their diverse overlap levels and develop a multi-task Meta-Weight-Net (MWN) to determine the corresponding weighted factors. Third, we jointly train the internal MWN model with the losses from the external HGNN model and train the external model with the weighted factors from the internal model. To evaluate the effectiveness of OMA-HGNN, we conducted experiments on six real-world datasets and benchmarked its perfor-mance against nine state-of-the-art methods for node classification. The results demonstrate that OMA-HGNN excels in learning superior node representations and outperforms these baselines.

SHyPar: A Spectral Coarsening Approach to Hypergraph Partitioning

State-of-the-art hypergraph partitioners utilize a multilevel paradigm to construct progressively coarser hypergraphs across multiple layers, guiding cut refinements at each level of the hierarchy. Traditionally, these partitioners employ heuristic methods for coarsening and do not consider the structural features of hypergraphs. In this work, we introduce a multilevel spectral framework, SHyPar, for partitioning large-scale hypergraphs by leveraging hyperedge effective resistances and flow-based community detection techniques. Inspired by the latest theoretical spectral clustering frameworks, such as HyperEF and HyperSF, SHyPar aims to decompose large hypergraphs into multiple subgraphs with few inter-partition hyperedges (cut size). A key component of SHyPar is a flow-based local clustering scheme for hypergraph coarsening, which incorporates a max-flow-based algorithm to produce clusters with substantially improved conductance. Additionally, SHyPar utilizes an effective resistance-based rating function for merging nodes that are strongly connected (coupled). Compared with existing state-of-the-art hypergraph partitioning methods, our extensive experimental results on real-world VLSI designs demonstrate that SHyPar can more effectively partition hypergraphs, achieving state-of-the-art solution quality.

VLSI Hypergraph Partitioning with Deep Learning

Partitioning is a known problem in computer science and is critical in chip design workflows, as advancements in this area can significantly influence design quality and efficiency. Deep Learning (DL) techniques, particularly those involving Graph Neural Networks (GNNs), have demonstrated strong performance in various node, edge, and graph prediction tasks using both inductive and transductive learning methods. A notable area of recent interest within GNNs are pooling layers and their application to graph partitioning. While these methods have yielded promising results across social, computational, and other random graphs, their effectiveness has not yet been explored in the context of VLSI hypergraph netlists. In this study, we introduce a new set of synthetic partitioning benchmarks that emulate real-world netlist characteristics and possess a known upper bound for solution cut quality. We distinguish these benchmarks with the prior work and evaluate existing state-of-the-art partitioning algorithms alongside GNN-based approaches, highlighting their respective advantages and disadvantages.

Hypergraphs as Weighted Directed Self-Looped Graphs: Spectral Properties, Clustering, Cheeger Inequality

Hypergraphs naturally arise when studying group relations and have been widely used in the field of machine learning. There has not been a unified formulation of hypergraphs, yet the recently proposed edge-dependent vertex weights (EDVW) modeling is one of the most generalized modeling methods of hypergraphs, i.e., most existing hypergraphs can be formulated as EDVW hypergraphs without any information loss to the best of our knowledge. However, the relevant algorithmic developments on EDVW hypergraphs remain nascent: compared to spectral graph theories, the formulations are incomplete, the spectral clustering algorithms are not well-developed, and one result regarding hypergraph Cheeger Inequality is even incorrect. To this end, deriving a unified random walk-based formulation, we propose our definitions of hypergraph Rayleigh Quotient, NCut, boundary/cut, volume, and conductance, which are consistent with the corresponding definitions on graphs. Then, we prove that the normalized hypergraph Laplacian is associated with the NCut value, which inspires our HyperClus-G algorithm for spectral clustering on EDVW hypergraphs. Finally, we prove that HyperClus-G can always find an approximately linearly optimal partitioning in terms of Both NCut and conductance. Additionally, we provide extensive experiments to validate our theoretical findings from an empirical perspective.

Geometry of the Space of Partitioned Networks: A Unified Theoretical and Computational Framework

Interactions and relations between objects may be pairwise or higher-order in nature, and so network-valued data are ubiquitous in the real world. The "space of networks", however, has a complex structure that cannot be adequately described using conventional statistical tools. We introduce a measure-theoretic formalism for modeling generalized network structures such as graphs, hypergraphs, or graphs whose nodes come with a partition into categorical classes. We then propose a metric that extends the Gromov-Wasserstein distance between graphs and the co-optimal transport distance between hypergraphs. We characterize the geometry of this space, thereby providing a unified theoretical treatment of generalized networks that encompasses the cases of pairwise, as well as higher-order, relations. In particular, we show that our metric is an Alexandrov space of non-negative curvature, and leverage this structure to define gradients for certain functionals commonly arising in geometric data analysis tasks. We extend our analysis to the setting where vertices have additional label information, and derive efficient computational schemes to use in practice. Equipped with these theoretical and computational tools, we demonstrate the utility of our framework in a suite of applications, including hypergraph alignment, clustering and dictionary learning from ensemble data, multi-omics alignment, as well as multiscale network alignment.

The Low-Degree Hardness of Finding Large Independent Sets in Sparse Random Hypergraphs

We study the algorithmic task of finding large independent sets in Erdos-Renyi $r$-uniform hypergraphs on $n$ vertices having average degree $d$. Krivelevich and Sudakov showed that the maximum independent set has density $\left(\frac{r\log d}{(r-1)d}\right)^{1/(r-1)}$. We show that the class of low-degree polynomial algorithms can find independent sets of density $\left(\frac{\log d}{(r-1)d}\right)^{1/(r-1)}$ but no larger. This extends and generalizes earlier results of Gamarnik and Sudan, Rahman and Virag, and Wein on graphs, and answers a question of Bal and Bennett. We conjecture that this statistical-computational gap holds for this problem. Additionally, we explore the universality of this gap by examining $r$-partite hypergraphs. A hypergraph $H=(V,E)$ is $r$-partite if there is a partition $V=V_1\cup\cdots\cup V_r$ such that each edge contains exactly one vertex from each set $V_i$. We consider the problem of finding large balanced independent sets (independent sets containing the same number of vertices in each partition) in random $r$-partite hypergraphs with $n$ vertices in each partition and average degree $d$. We prove that the maximum balanced independent set has density $\left(\frac{r\log d}{(r-1)d}\right)^{1/(r-1)}$ asymptotically. Furthermore, we prove an analogous low-degree computational threshold of $\left(\frac{\log d}{(r-1)d}\right)^{1/(r-1)}$. Our results recover and generalize recent work of Perkins and the second author on bipartite graphs. While the graph case has been extensively studied, this work is the first to consider statistical-computational gaps of optimization problems on random hypergraphs. Our results suggest that these gaps persist for larger uniformities as well as across many models. A somewhat surprising aspect of the gap for balanced independent sets is that the algorithm achieving the lower bound is a simple degree-1 polynomial.