Chunqi Yang
BIPNN: Learning to Solve Binary Integer Programming via Hypergraph Neural Networks
May 27, 2025Abstract:Binary (0-1) integer programming (BIP) is pivotal in scientific domains requiring discrete decision-making. As the advance of AI computing, recent works explore neural network-based solvers for integer linear programming (ILP) problems. Yet, they lack scalability for tackling nonlinear challenges. To handle nonlinearities, state-of-the-art Branch-and-Cut solvers employ linear relaxations, leading to exponential growth in auxiliary variables and severe computation limitations. To overcome these limitations, we propose BIPNN (Binary Integer Programming Neural Network), an unsupervised learning framework to solve nonlinear BIP problems via hypergraph neural networks (HyperGNN). Specifically, BIPNN reformulates BIPs-constrained, discrete, and nonlinear (sin, log, exp) optimization problems-into unconstrained, differentiable, and polynomial loss functions. The reformulation stems from the observation of a precise one-to-one mapping between polynomial BIP objectives and hypergraph structures, enabling the unsupervised training of HyperGNN to optimize BIP problems in an end-to-end manner. On this basis, we propose a GPU-accelerated and continuous-annealing-enhanced training pipeline for BIPNN. The pipeline enables BIPNN to optimize large-scale nonlinear terms in BIPs fully in parallel via straightforward gradient descent, thus significantly reducing the training cost while ensuring the generation of discrete, high-quality solutions. Extensive experiments on synthetic and real-world datasets highlight the superiority of our approach.
Deep k-grouping: An Unsupervised Learning Framework for Combinatorial Optimization on Graphs and Hypergraphs
May 27, 2025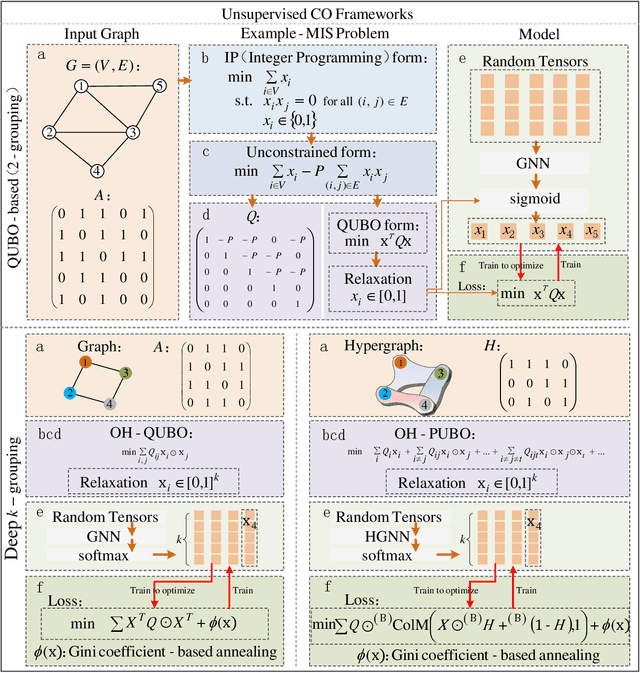

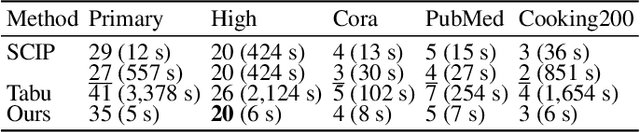
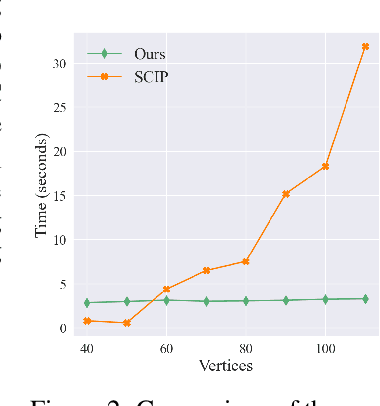
Abstract:Along with AI computing shining in scientific discovery, its potential in the combinatorial optimization (CO) domain has also emerged in recent years. Yet, existing unsupervised neural network solvers struggle to solve $k$-grouping problems (e.g., coloring, partitioning) on large-scale graphs and hypergraphs, due to limited computational frameworks. In this work, we propose Deep $k$-grouping, an unsupervised learning-based CO framework. Specifically, we contribute: Novel one-hot encoded polynomial unconstrained binary optimization (OH-PUBO), a formulation for modeling k-grouping problems on graphs and hypergraphs (e.g., graph/hypergraph coloring and partitioning); GPU-accelerated algorithms for large-scale k-grouping CO problems. Deep $k$-grouping employs the relaxation of large-scale OH-PUBO objectives as differentiable loss functions and trains to optimize them in an unsupervised manner. To ensure scalability, it leverages GPU-accelerated algorithms to unify the training pipeline; A Gini coefficient-based continuous relaxation annealing strategy to enforce discreteness of solutions while preventing convergence to local optima. Experimental results demonstrate that Deep $k$-grouping outperforms existing neural network solvers and classical heuristics such as SCIP and Tabu.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge