Deep k-grouping: An Unsupervised Learning Framework for Combinatorial Optimization on Graphs and Hypergraphs

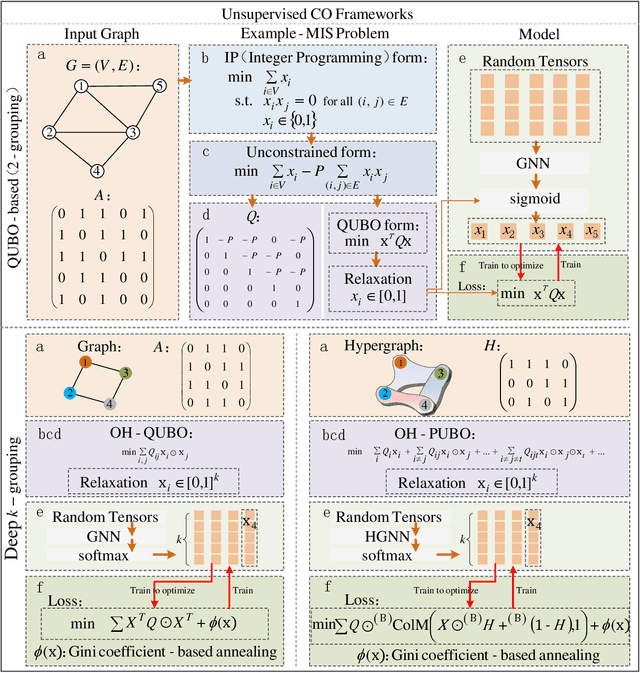
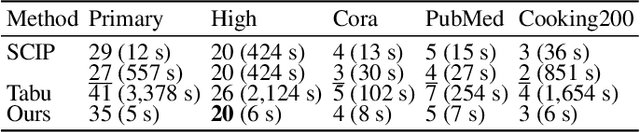
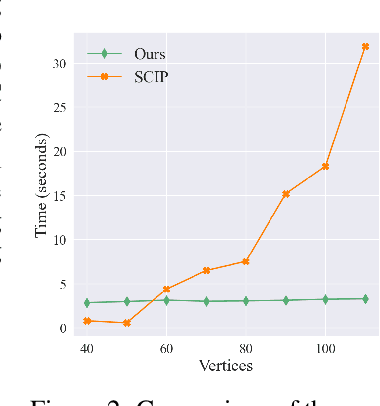
Along with AI computing shining in scientific discovery, its potential in the combinatorial optimization (CO) domain has also emerged in recent years. Yet, existing unsupervised neural network solvers struggle to solve $k$-grouping problems (e.g., coloring, partitioning) on large-scale graphs and hypergraphs, due to limited computational frameworks. In this work, we propose Deep $k$-grouping, an unsupervised learning-based CO framework. Specifically, we contribute: Novel one-hot encoded polynomial unconstrained binary optimization (OH-PUBO), a formulation for modeling k-grouping problems on graphs and hypergraphs (e.g., graph/hypergraph coloring and partitioning); GPU-accelerated algorithms for large-scale k-grouping CO problems. Deep $k$-grouping employs the relaxation of large-scale OH-PUBO objectives as differentiable loss functions and trains to optimize them in an unsupervised manner. To ensure scalability, it leverages GPU-accelerated algorithms to unify the training pipeline; A Gini coefficient-based continuous relaxation annealing strategy to enforce discreteness of solutions while preventing convergence to local optima. Experimental results demonstrate that Deep $k$-grouping outperforms existing neural network solvers and classical heuristics such as SCIP and Tabu.