DCatalyst: A Unified Accelerated Framework for Decentralized Optimization

We study decentralized optimization over a network of agents, modeled as graphs, with no central server. The goal is to minimize $f+r$, where $f$ represents a (strongly) convex function averaging the local agents' losses, and $r$ is a convex, extended-value function. We introduce DCatalyst, a unified black-box framework that integrates Nesterov acceleration into decentralized optimization algorithms. %, enhancing their performance. At its core, DCatalyst operates as an \textit{inexact}, \textit{momentum-accelerated} proximal method (forming the outer loop) that seamlessly incorporates any selected decentralized algorithm (as the inner loop). We demonstrate that DCatalyst achieves optimal communication and computational complexity (up to log-factors) across various decentralized algorithms and problem instances. Notably, it extends acceleration capabilities to problem classes previously lacking accelerated solution methods, thereby broadening the effectiveness of decentralized methods. On the technical side, our framework introduce the {\it inexact estimating sequences}--a novel extension of the well-known Nesterov's estimating sequences, tailored for the minimization of composite losses in decentralized settings. This method adeptly handles consensus errors and inexact solutions of agents' subproblems, challenges not addressed by existing models.

Enhancing Convergence of Decentralized Gradient Tracking under the KL Property

We study decentralized multiagent optimization over networks, modeled as undirected graphs. The optimization problem consists of minimizing a nonconvex smooth function plus a convex extended-value function, which enforces constraints or extra structure on the solution (e.g., sparsity, low-rank). We further assume that the objective function satisfies the Kurdyka-{\L}ojasiewicz (KL) property, with given exponent $\theta\in [0,1)$. The KL property is satisfied by several (nonconvex) functions of practical interest, e.g., arising from machine learning applications; in the centralized setting, it permits to achieve strong convergence guarantees. Here we establish convergence of the same type for the notorious decentralized gradient-tracking-based algorithm SONATA. Specifically, $\textbf{(i)}$ when $\theta\in (0,1/2]$, the sequence generated by SONATA converges to a stationary solution of the problem at R-linear rate;$ \textbf{(ii)} $when $\theta\in (1/2,1)$, sublinear rate is certified; and finally $\textbf{(iii)}$ when $\theta=0$, the iterates will either converge in a finite number of steps or converges at R-linear rate. This matches the convergence behavior of centralized proximal-gradient algorithms except when $\theta=0$. Numerical results validate our theoretical findings.

Optimal Gradient Sliding and its Application to Distributed Optimization Under Similarity

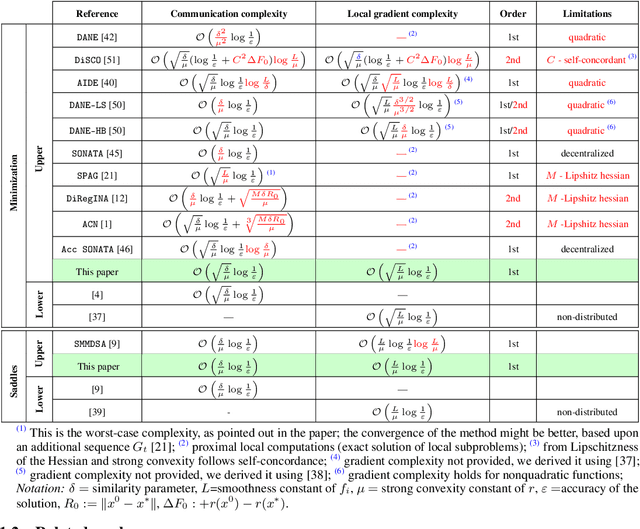
We study structured convex optimization problems, with additive objective $r:=p + q$, where $r$ is ($\mu$-strongly) convex, $q$ is $L_q$-smooth and convex, and $p$ is $L_p$-smooth, possibly nonconvex. For such a class of problems, we proposed an inexact accelerated gradient sliding method that can skip the gradient computation for one of these components while still achieving optimal complexity of gradient calls of $p$ and $q$, that is, $\mathcal{O}(\sqrt{L_p/\mu})$ and $\mathcal{O}(\sqrt{L_q/\mu})$, respectively. This result is much sharper than the classic black-box complexity $\mathcal{O}(\sqrt{(L_p+L_q)/\mu})$, especially when the difference between $L_q$ and $L_q$ is large. We then apply the proposed method to solve distributed optimization problems over master-worker architectures, under agents' function similarity, due to statistical data similarity or otherwise. The distributed algorithm achieves for the first time lower complexity bounds on {\it both} communication and local gradient calls, with the former having being a long-standing open problem. Finally the method is extended to distributed saddle-problems (under function similarity) by means of solving a class of variational inequalities, achieving lower communication and computation complexity bounds.

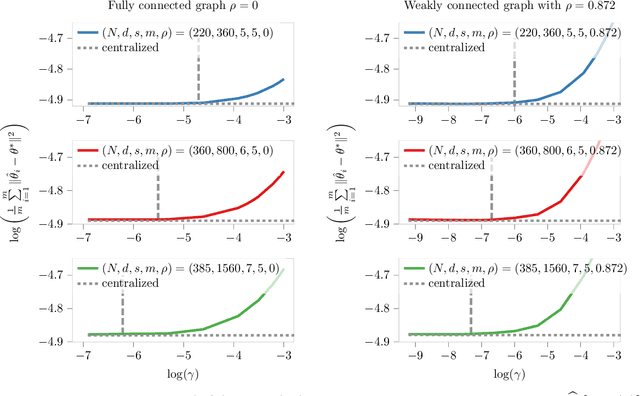
High-Dimensional Inference over Networks: Linear Convergence and Statistical Guarantees

We study sparse linear regression over a network of agents, modeled as an undirected graph and no server node. The estimation of the $s$-sparse parameter is formulated as a constrained LASSO problem wherein each agent owns a subset of the $N$ total observations. We analyze the convergence rate and statistical guarantees of a distributed projected gradient tracking-based algorithm under high-dimensional scaling, allowing the ambient dimension $d$ to grow with (and possibly exceed) the sample size $N$. Our theory shows that, under standard notions of restricted strong convexity and smoothness of the loss functions, suitable conditions on the network connectivity and algorithm tuning, the distributed algorithm converges globally at a {\it linear} rate to an estimate that is within the centralized {\it statistical precision} of the model, $O(s\log d/N)$. When $s\log d/N=o(1)$, a condition necessary for statistical consistency, an $\varepsilon$-optimal solution is attained after $\mathcal{O}(\kappa \log (1/\varepsilon))$ gradient computations and $O (\kappa/(1-\rho) \log (1/\varepsilon))$ communication rounds, where $\kappa$ is the restricted condition number of the loss function and $\rho$ measures the network connectivity. The computation cost matches that of the centralized projected gradient algorithm despite having data distributed; whereas the communication rounds reduce as the network connectivity improves. Overall, our study reveals interesting connections between statistical efficiency, network connectivity \& topology, and convergence rate in high dimensions.

Distributed Sparse Regression via Penalization

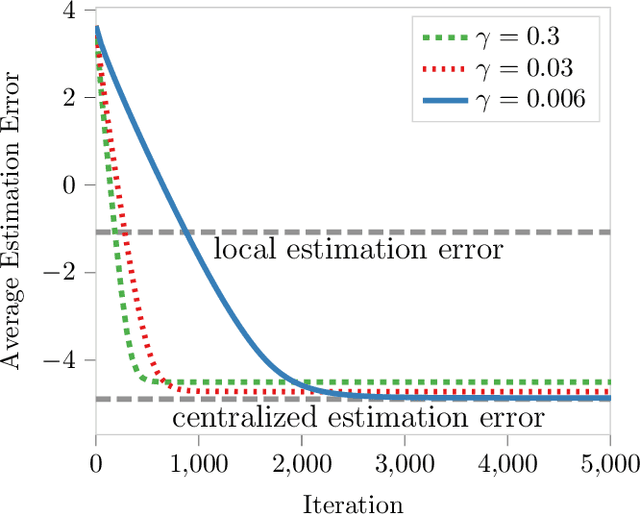
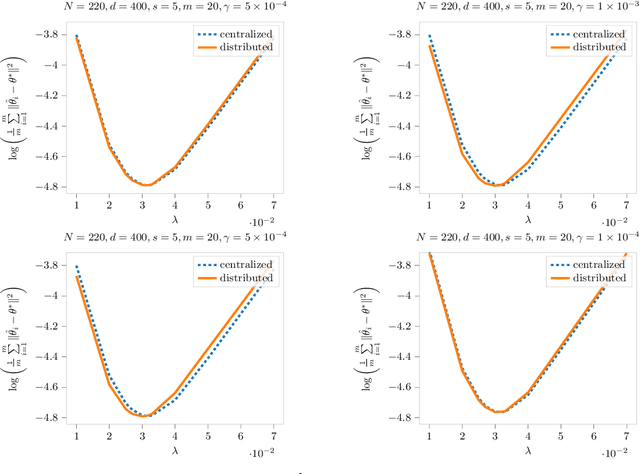
We study sparse linear regression over a network of agents, modeled as an undirected graph (with no centralized node). The estimation problem is formulated as the minimization of the sum of the local LASSO loss functions plus a quadratic penalty of the consensus constraint -- the latter being instrumental to obtain distributed solution methods. While penalty-based consensus methods have been extensively studied in the optimization literature, their statistical and computational guarantees in the high dimensional setting remain unclear. This work provides an answer to this open problem. Our contribution is two-fold. First, we establish statistical consistency of the estimator: under a suitable choice of the penalty parameter, the optimal solution of the penalized problem achieves near optimal minimax rate $\mathcal{O}(s \log d/N)$ in $\ell_2$-loss, where $s$ is the sparsity value, $d$ is the ambient dimension, and $N$ is the total sample size in the network -- this matches centralized sample rates. Second, we show that the proximal-gradient algorithm applied to the penalized problem, which naturally leads to distributed implementations, converges linearly up to a tolerance of the order of the centralized statistical error -- the rate scales as $\mathcal{O}(d)$, revealing an unavoidable speed-accuracy dilemma.Numerical results demonstrate the tightness of the derived sample rate and convergence rate scalings.

Acceleration in Distributed Optimization Under Similarity

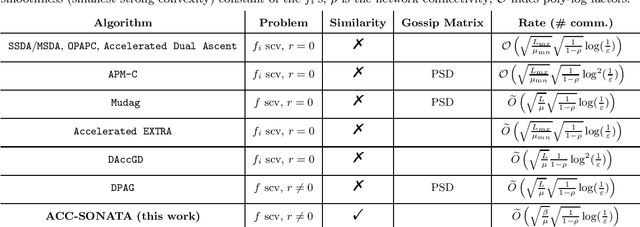
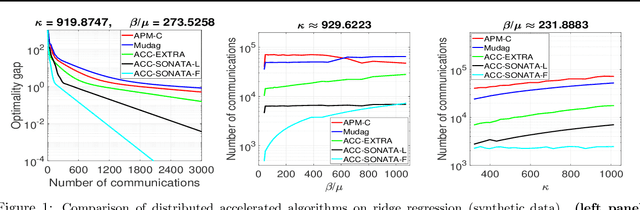
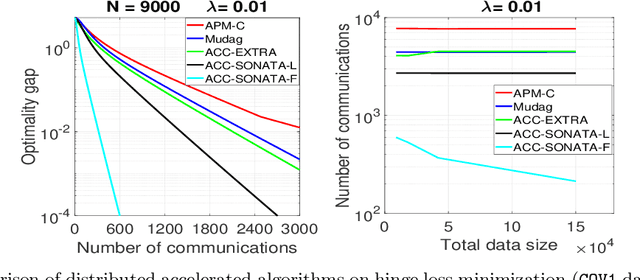
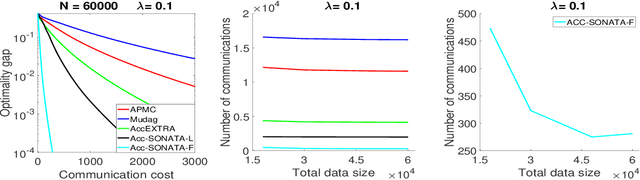
We study distributed (strongly convex) optimization problems over a network of agents, with no centralized nodes. The loss functions of the agents are assumed to be similar, due to statistical data similarity or otherwise. In order to reduce the number of communications to reach a solution accuracy, we proposed a preconditioned, accelerated distributed method. An $\varepsilon$-solution is achieved in $\tilde{\mathcal{O}}\big(\sqrt{\frac{\beta/\mu}{(1-\rho)}}\log1/\varepsilon\big)$ number of communications steps, where $\beta/\mu$ is the relative condition number between the global and local loss functions, and $\rho$ characterizes the connectivity of the network. This rate matches (up to poly-log factors) for the first time lower complexity communication bounds of distributed gossip-algorithms applied to the class of problems of interest. Numerical results show significant communication savings with respect to existing accelerated distributed schemes, especially when solving ill-conditioned problems.

Finite-Bit Quantization For Distributed Algorithms With Linear Convergence

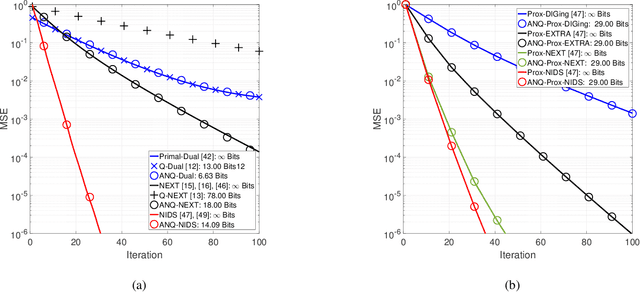
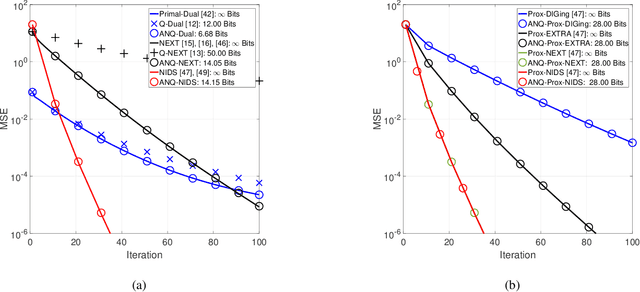
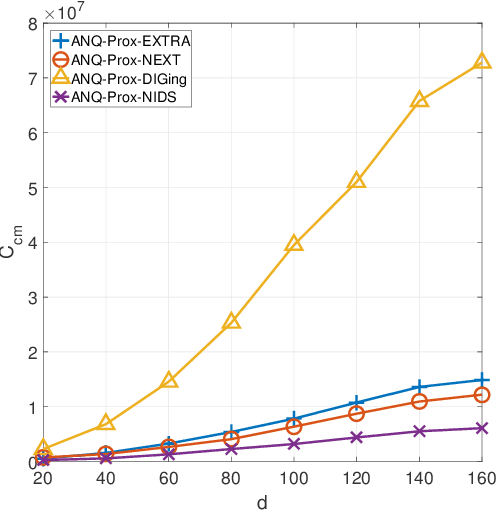
This paper studies distributed algorithms for (strongly convex) composite optimization problems over mesh networks, subject to quantized communications. Instead of focusing on a specific algorithmic design, we propose a black-box model casting distributed algorithms in the form of fixed-point iterates, converging at linear rate. The algorithmic model is coupled with a novel (random) Biased Compression (BC-)rule on the quantizer design, which preserves linear convergence. A new quantizer coupled with a communication-efficient encoding scheme is also proposed, which efficiently implements the BC-rule using a finite number of bits. This contrasts with most of existing quantization rules, whose implementation calls for an infinite number of bits. A unified communication complexity analysis is developed for the black-box model, determining the average number of bit required to reach a solution of the optimization problem within the required accuracy. Numerical results validate our theoretical findings and show that distributed algorithms equipped with the proposed quantizer have more favorable communication complexity than algorithms using existing quantization rules.

Distributed Saddle-Point Problems Under Similarity

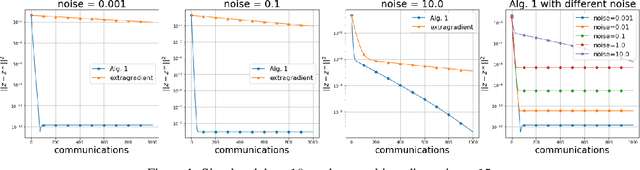
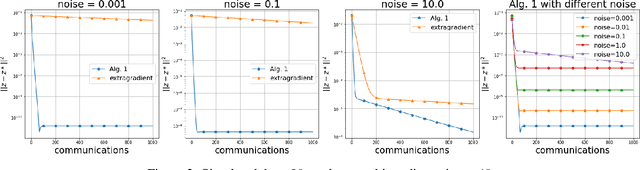
We study solution methods for (strongly-)convex-(strongly)-concave Saddle-Point Problems (SPPs) over networks of two type - master/workers (thus centralized) architectures and meshed (thus decentralized) networks. The local functions at each node are assumed to be similar, due to statistical data similarity or otherwise. We establish lower complexity bounds for a fairly general class of algorithms solving the SPP. We show that a given suboptimality $\epsilon>0$ is achieved over master/workers networks in $\Omega\big(\Delta\cdot \delta/\mu\cdot \log (1/\varepsilon)\big)$ rounds of communications, where $\delta>0$ measures the degree of similarity of the local functions, $\mu$ is their strong convexity constant, and $\Delta$ is the diameter of the network. The lower communication complexity bound over meshed networks reads $\Omega\big(1/{\sqrt{\rho}} \cdot {\delta}/{\mu}\cdot\log (1/\varepsilon)\big)$, where $\rho$ is the (normalized) eigengap of the gossip matrix used for the communication between neighbouring nodes. We then propose algorithms matching the lower bounds over either types of networks (up to log-factors). We assess the effectiveness of the proposed algorithms on a robust logistic regression problem.

Kernel Bi-Linear Modeling for Reconstructing Data on Manifolds: The Dynamic-MRI Case

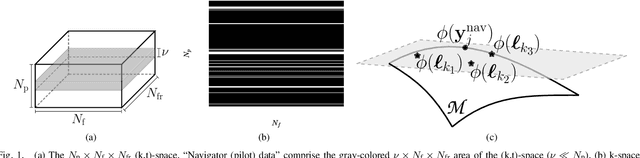
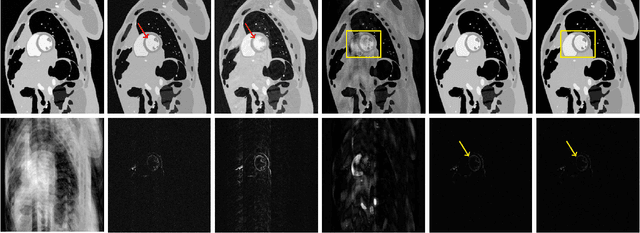
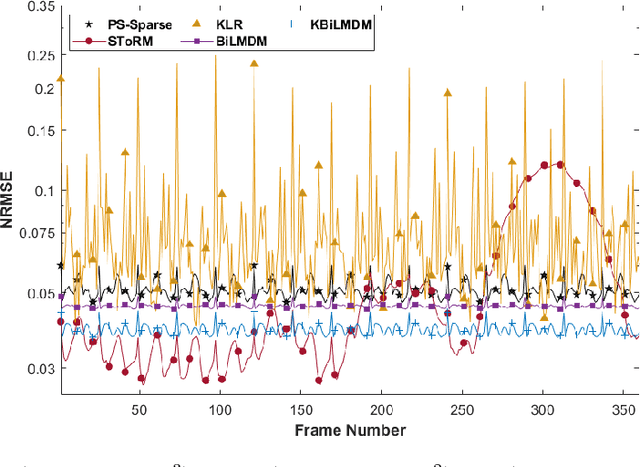
This paper establishes a kernel-based framework for reconstructing data on manifolds, tailored to fit the dynamic-(d)MRI-data recovery problem. The proposed methodology exploits simple tangent-space geometries of manifolds in reproducing kernel Hilbert spaces and follows classical kernel-approximation arguments to form the data-recovery task as a bi-linear inverse problem. Departing from mainstream approaches, the proposed methodology uses no training data, employs no graph Laplacian matrix to penalize the optimization task, uses no costly (kernel) pre-imaging step to map feature points back to the input space, and utilizes complex-valued kernel functions to account for k-space data. The framework is validated on synthetically generated dMRI data, where comparisons against state-of-the-art schemes highlight the rich potential of the proposed approach in data-recovery problems.

Accelerated Primal-Dual Algorithms for Distributed Smooth Convex Optimization over Networks

This paper proposes a novel family of primal-dual-based distributed algorithms for smooth, convex, multi-agent optimization over networks that uses only gradient information and gossip communications. The algorithms can also employ acceleration on the computation and communications. We provide a unified analysis of their convergence rate, measured in terms of the Bregman distance associated to the saddle point reformation of the distributed optimization problem. When acceleration is employed, the rate is shown to be optimal, in the sense that it matches (under the proposed metric) existing complexity lower bounds of distributed algorithms applicable to such a class of problem and using only gradient information and gossip communications. Preliminary numerical results on distributed least-square regression problems show that the proposed algorithm compares favorably on existing distributed schemes.