Yinan Li
Clover: Towards A Unified Video-Language Alignment and Fusion Model
Jul 16, 2022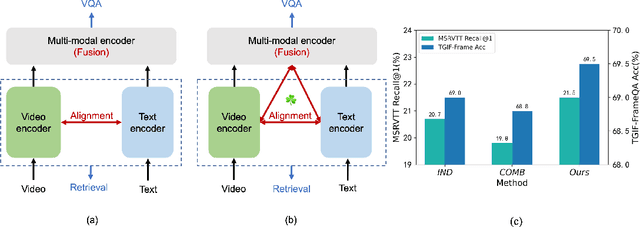
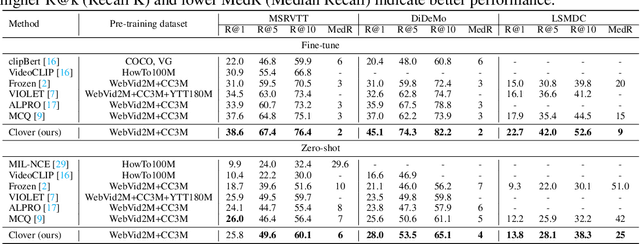
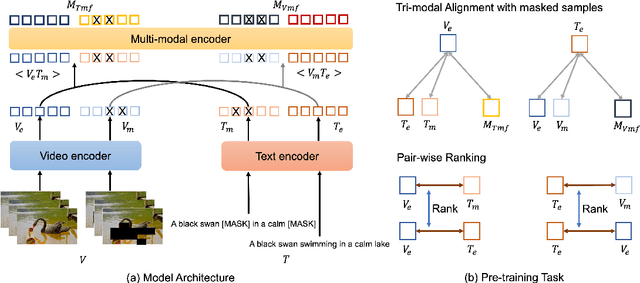
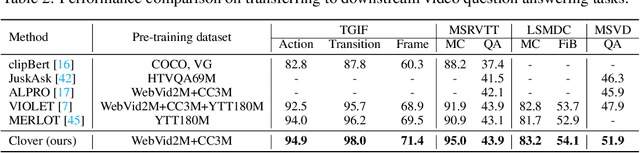
Abstract:Building a universal video-language model for solving various video understanding tasks (e.g., text-video retrieval, video question answering) is an open challenge to the machine learning field. Towards this goal, most recent attempts train the models, usually consisting of uni-modal and cross-modal feature encoders, with supervised or pair-wise contrastive pre-text tasks. Though offering attractive generality, the resulted models have to compromise between efficiency and performance. We argue the flaws are caused by their pre-training strategies\textemdash they cannot well align and fuse features from different modalities simultaneously. We then introduce Clover -- a Correlated Video-Language pre-training method -- towards a universal video-language model for solving multiple video understanding tasks with neither performance nor efficiency compromise. It improves cross-modal feature alignment and fusion via a novel tri-modal alignment pre-training task. Additionally, we propose to enhance the tri-modal alignment via incorporating learning from masked samples and a novel pair-wise ranking loss. Clover demonstrates outstanding generality. It establishes new state-of-the-arts on multiple downstream tasks, including three retrieval tasks for both zero-shot and fine-tuning settings, and eight video question answering tasks. Codes and pre-trained models will be released at https://github.com/LeeYN-43/Clover.
Adaptive Noisy Data Augmentation for Regularized Estimation and Inference in Generalized Linear Models
Apr 18, 2022
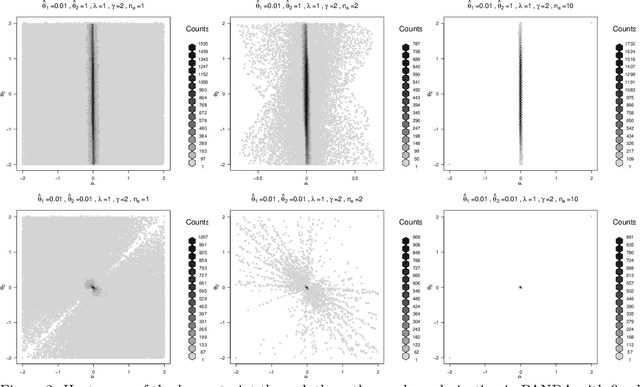
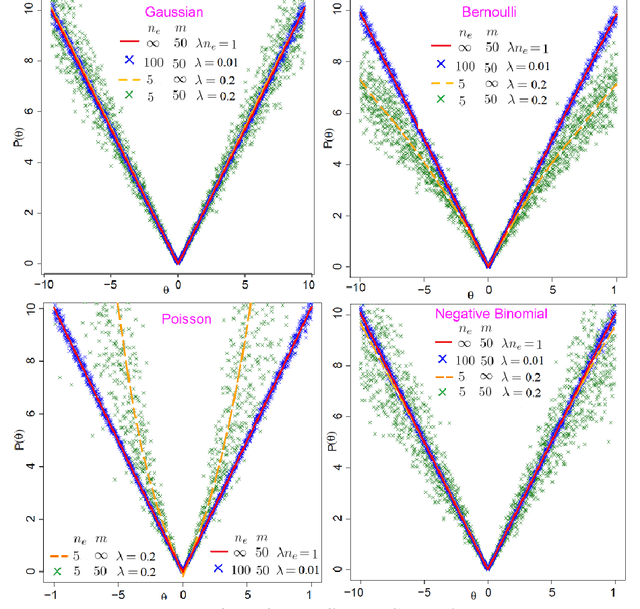
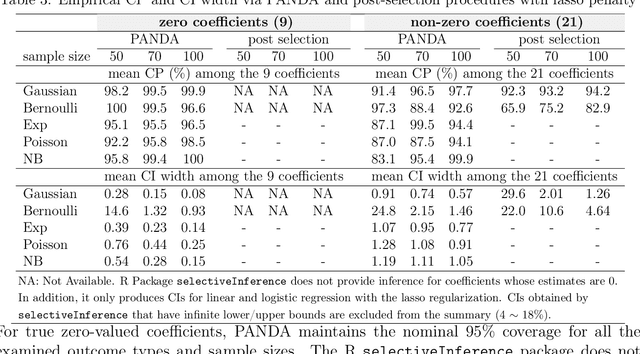
Abstract:We propose the AdaPtive Noise Augmentation (PANDA) procedure to regularize the estimation and inference of generalized linear models (GLMs). PANDA iteratively optimizes the objective function given noise augmented data until convergence to obtain the regularized model estimates. The augmented noises are designed to achieve various regularization effects, including $l_0$, bridge (lasso and ridge included), elastic net, adaptive lasso, and SCAD, as well as group lasso and fused ridge. We examine the tail bound of the noise-augmented loss function and establish the almost sure convergence of the noise-augmented loss function and its minimizer to the expected penalized loss function and its minimizer, respectively. We derive the asymptotic distributions for the regularized parameters, based on which, inferences can be obtained simultaneously with variable selection. PANDA exhibits ensemble learning behaviors that help further decrease the generalization error. Computationally, PANDA is easy to code, leveraging existing software for implementing GLMs, without resorting to complicated optimization techniques. We demonstrate the superior or similar performance of PANDA against the existing approaches of the same type of regularizers in simulated and real-life data. We show that the inferences through PANDA achieve nominal or near-nominal coverage and are far more efficient compared to a popular existing post-selection procedure.
Noise-Augmented Privacy-Preserving Empirical Risk Minimization with Dual-purpose Regularizer and Privacy Budget Retrieval and Recycling
Oct 16, 2021
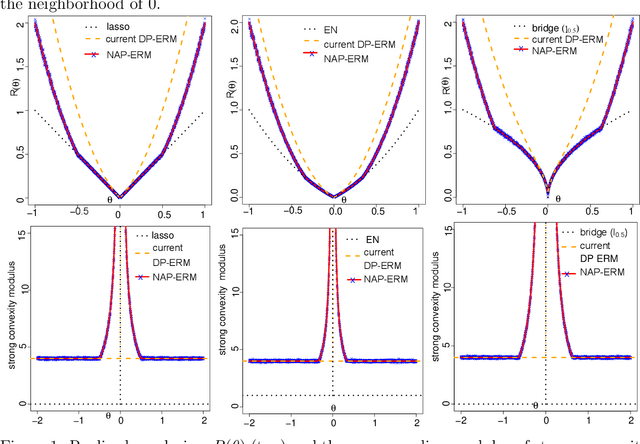
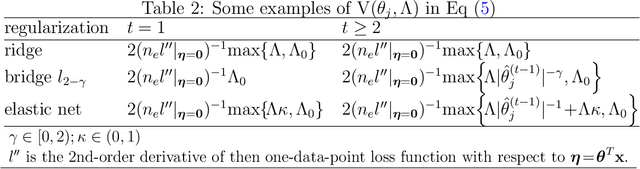
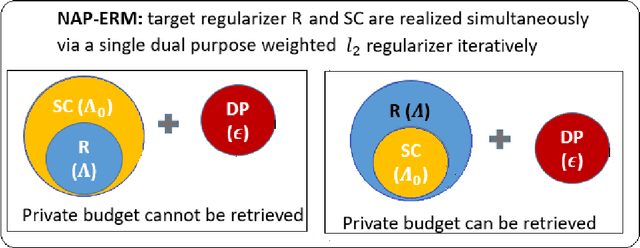
Abstract:We propose Noise-Augmented Privacy-Preserving Empirical Risk Minimization (NAPP-ERM) that solves ERM with differential privacy guarantees. Existing privacy-preserving ERM approaches may be subject to over-regularization with the employment of an l2 term to achieve strong convexity on top of the target regularization. NAPP-ERM improves over the current approaches and mitigates over-regularization by iteratively realizing target regularization through appropriately designed augmented data and delivering strong convexity via a single adaptively weighted dual-purpose l2 regularizer. When the target regularization is for variable selection, we propose a new regularizer that achieves both privacy and sparsity guarantees simultaneously. Finally, we propose a strategy to retrieve privacy budget when the strong convexity requirement is met, which can be returned to users such that the DP of ERM is guaranteed at a lower privacy cost than originally planned, or be recycled to the ERM optimization procedure to reduce the injected DP noise and improve the utility of DP-ERM. From an implementation perspective, NAPP-ERM can be achieved by optimizing a non-perturbed object function given noise-augmented data and can thus leverage existing tools for non-private ERM optimization. We illustrate through extensive experiments the mitigation effect of the over-regularization and private budget retrieval by NAPP-ERM on variable selection and prediction.
Improved Algorithms for Efficient Active Learning Halfspaces with Massart and Tsybakov noise
Feb 10, 2021Abstract:We develop a computationally-efficient PAC active learning algorithm for $d$-dimensional homogeneous halfspaces that can tolerate Massart noise~\citep{massart2006risk} and Tsybakov noise~\citep{tsybakov2004optimal}. Specialized to the $\eta$-Massart noise setting, our algorithm achieves an information-theoretic optimal label complexity of $\tilde{O}\left( \frac{d}{(1-2\eta)^2} \mathrm{polylog}(\frac1\epsilon) \right)$ under a wide range of unlabeled data distributions (specifically, the family of "structured distributions" defined in~\citet{diakonikolas2020polynomial}). Under the more challenging Tsybakov noise condition, we identify two subfamilies of noise conditions, under which our algorithm achieves computational efficiency and provide label complexity guarantees strictly lower than passive learning algorithms.
Qd-tree: Learning Data Layouts for Big Data Analytics
Apr 22, 2020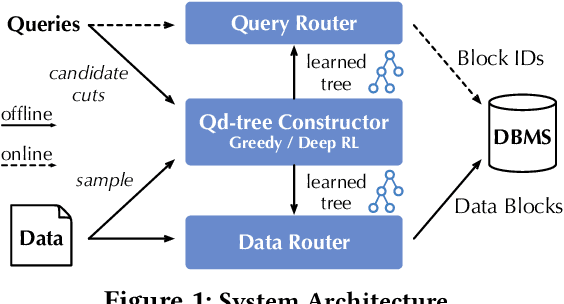

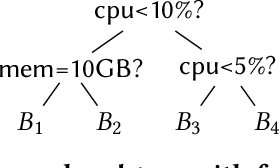
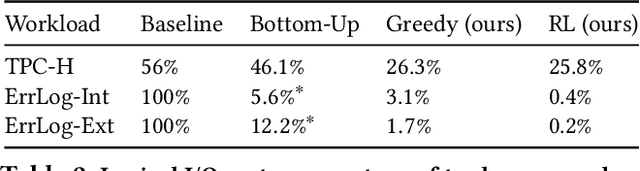
Abstract:Corporations today collect data at an unprecedented and accelerating scale, making the need to run queries on large datasets increasingly important. Technologies such as columnar block-based data organization and compression have become standard practice in most commercial database systems. However, the problem of best assigning records to data blocks on storage is still open. For example, today's systems usually partition data by arrival time into row groups, or range/hash partition the data based on selected fields. For a given workload, however, such techniques are unable to optimize for the important metric of the number of blocks accessed by a query. This metric directly relates to the I/O cost, and therefore performance, of most analytical queries. Further, they are unable to exploit additional available storage to drive this metric down further. In this paper, we propose a new framework called a query-data routing tree, or qd-tree, to address this problem, and propose two algorithms for their construction based on greedy and deep reinforcement learning techniques. Experiments over benchmark and real workloads show that a qd-tree can provide physical speedups of more than an order of magnitude compared to current blocking schemes, and can reach within 2X of the lower bound for data skipping based on selectivity, while providing complete semantic descriptions of created blocks.
Continuous Motion Planning with Temporal Logic Specifications using Deep Neural Networks
Apr 02, 2020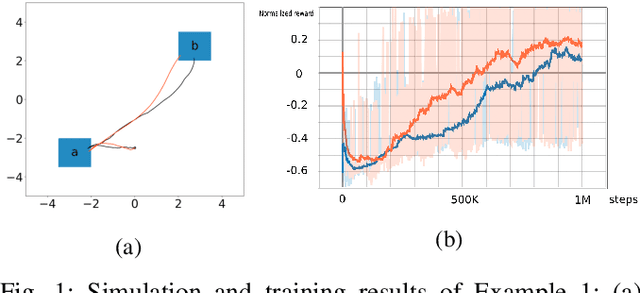
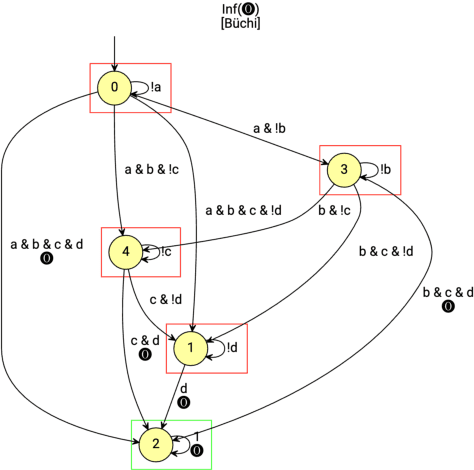
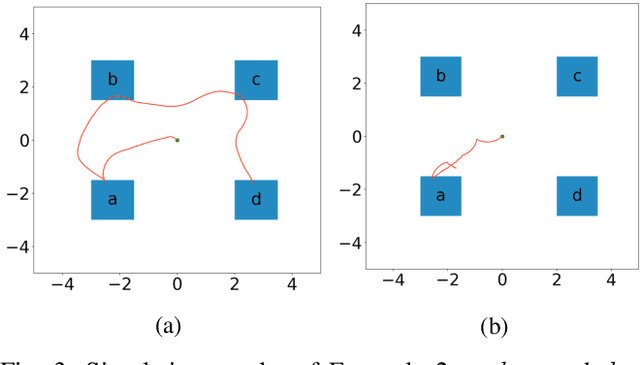
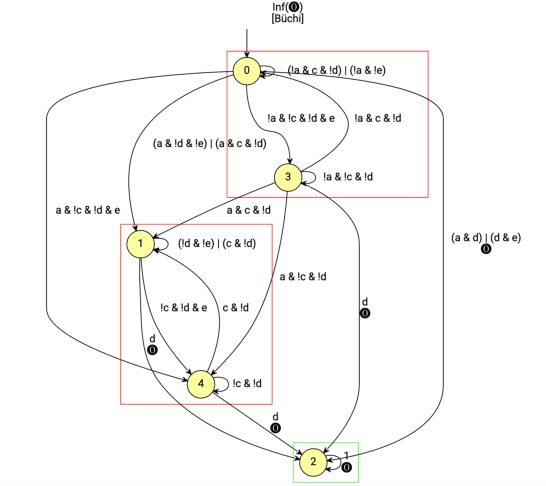
Abstract:In this paper, we propose a model-free reinforcement learning method to synthesize control policies for motion planning problems for continuous states and actions. The robot is modelled as a labeled Markov decision process (MDP) with continuous state and action spaces. Linear temporal logics (LTL) are used to specify high-level tasks. We then train deep neural networks to approximate the value function and policy using an actor-critic reinforcement learning method. The LTL specification is converted into an annotated limit-deterministic B\"uchi automaton (LDBA) for continuously shaping the reward so that dense reward is available during training. A naive way of solving a motion planning problem with LTL specifications using reinforcement learning is to sample a trajectory and, if the trajectory satisfies the entire LTL formula then we assign a high reward for training. However, the sampling complexity needed to find such a trajectory is too high when we have a complex LTL formula for continuous state and action spaces. As a result, it is very unlikely that we get enough reward for training if all sample trajectories start from the initial state in the automata. In this paper, we propose a method that samples not only an initial state from the state space, but also an arbitrary state in the automata at the beginning of each training episode. We test our algorithm in simulation using a car-like robot and find out that our method can learn policies for different working configurations and LTL specifications successfully.
ALEX: An Updatable Adaptive Learned Index
May 21, 2019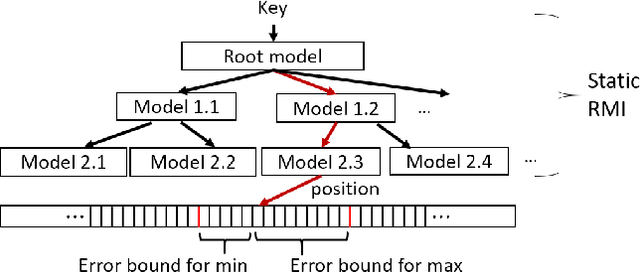

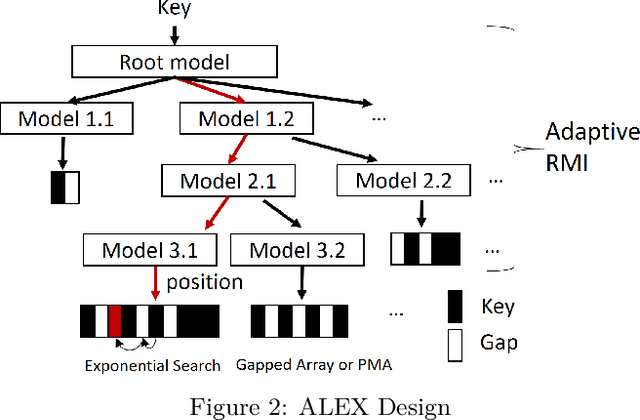
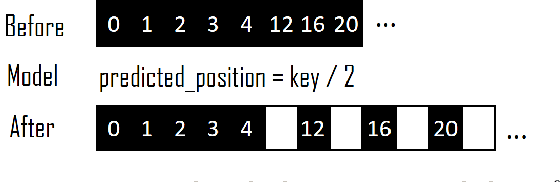
Abstract:Recent work on "learned indexes" has revolutionized the way we look at the decades-old field of DBMS indexing. The key idea is that indexes are "models" that predict the position of a key in a dataset. Indexes can, thus, be learned. The original work by Kraska et al. shows surprising results in terms of search performance and space requirements: A learned index beats a B+Tree by a factor of up to three in search time and by an order of magnitude in memory footprint, however it is limited to static, read-only workloads. This paper presents a new class of learned indexes called ALEX which addresses issues that arise when implementing dynamic, updatable learned indexes. Compared to the learned index from Kraska et al., ALEX has up to 3000X lower space requirements, but has up to 2.7X higher search performance on static workloads. Compared to a B+Tree, ALEX achieves up to 3.5X and 3.3X higher performance on static and some dynamic workloads, respectively, with up to 5 orders of magnitude smaller index size. Our detailed experiments show that ALEX presents a key step towards making learned indexes practical for a broader class of database workloads with dynamic updates.
Reactive Task and Motion Planning for Robust Whole-Body Dynamic Locomotion in Constrained Environments
Nov 11, 2018

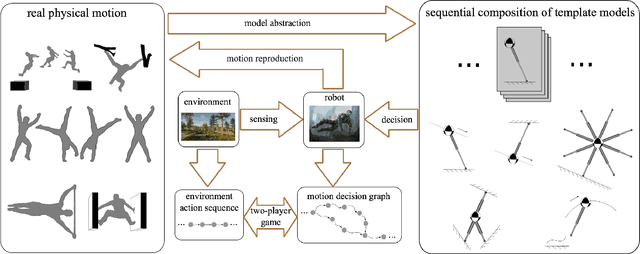
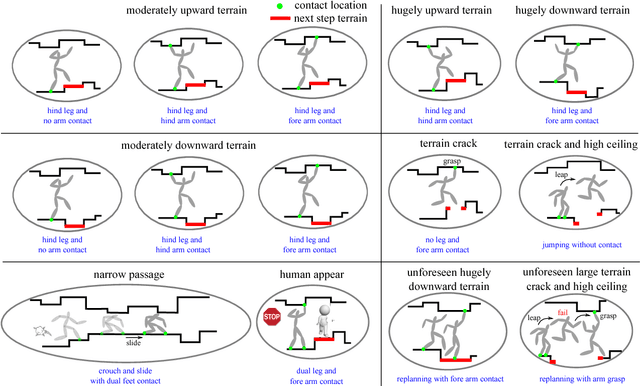
Abstract:Contact-based decision and planning methods are becoming increasingly important to endow higher levels of autonomy for legged robots. Formal synthesis methods derived from symbolic systems have great potential for reasoning about high-level locomotion decisions and achieving complex maneuvering behaviors with correctness guarantees. This study takes a first step toward formally devising an architecture composed of task planning and control of whole-body dynamic locomotion behaviors in constrained and dynamically changing environments. At the high level, we formulate a two-player temporal logic game between the multi-limb locomotion planner and its dynamic environment to synthesize a winning strategy that delivers symbolic locomotion actions. These locomotion actions satisfy the desired high-level task specifications expressed in a fragment of temporal logic. Those actions are sent to a robust finite transition system that synthesizes a locomotion controller that fulfills state reachability constraints. This controller is further executed via a low-level motion planner that generates feasible locomotion trajectories. We construct a set of dynamic locomotion models for legged robots to serve as a template library for handling diverse environmental events. We devise a replanning strategy that takes into consideration sudden environmental changes or large state disturbances to increase the robustness of the resulting locomotion behaviors. We formally prove the correctness of the layered locomotion framework guaranteeing a robust implementation by the motion planning layer. Simulations of reactive locomotion behaviors in diverse environments indicate that our framework has the potential to serve as a theoretical foundation for intelligent locomotion behaviors.
Panda: AdaPtive Noisy Data Augmentation for Regularization of Undirected Graphical Models
Oct 11, 2018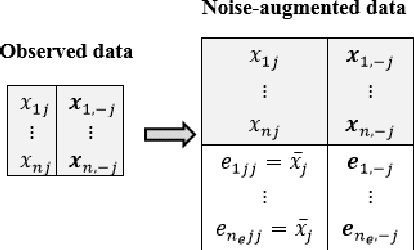
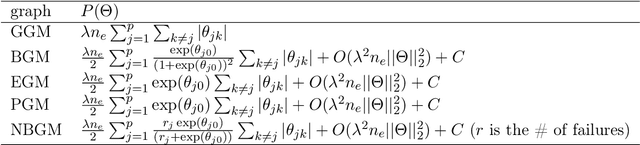
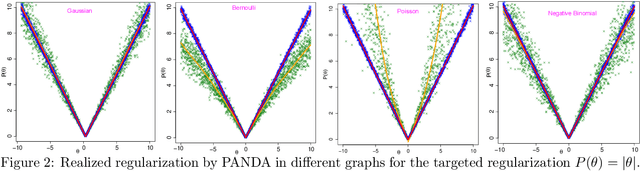
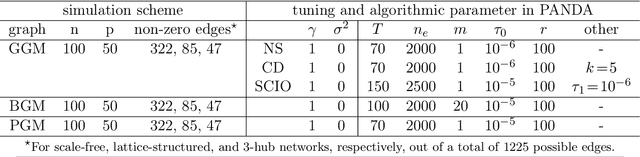
Abstract:We propose PANDA, an AdaPtive Noise Augmentation technique to regularize estimating and constructing undirected graphical models (UGMs). PANDA iteratively solves MLEs given noise augmented data in the regression-based framework until convergence to achieve the designed regularization effects. The augmented noises can be designed to achieve various regularization effects on graph estimation, including the bridge, elastic net, adaptive lasso, and SCAD penalization; it can also offer group lasso and fused ridge when some nodes belong to the same group. We establish theoretically that the noise-augmented loss functions and its minimizer converge almost surely to the expected penalized loss function and its minimizer, respectively. We derive the asymptotic distributions for the regularized regression coefficients through PANDA in GLMs, based on which, the inferences for the parameters can be obtained simultaneously with variable selection. Our empirical results suggest the inferences achieve nominal or near-nominal coverage and are far more efficient compared to some existing post-selection procedures. On the algorithm level, PANDA can be easily programmed in any standard software without resorting to complicated optimization techniques. We show the non-inferior performance of PANDA in constructing graphs of different types in simulation studies and also apply PANDA to the autism spectrum disorder data to construct a mixed-node graph.
Whiteout: Gaussian Adaptive Noise Regularization in Deep Neural Networks
May 09, 2018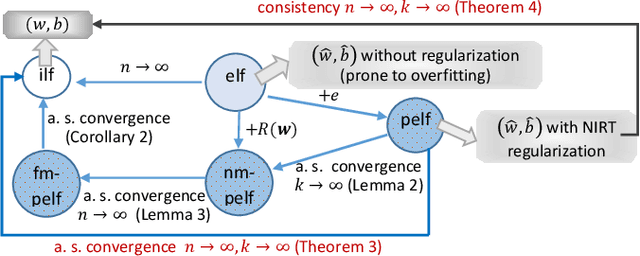
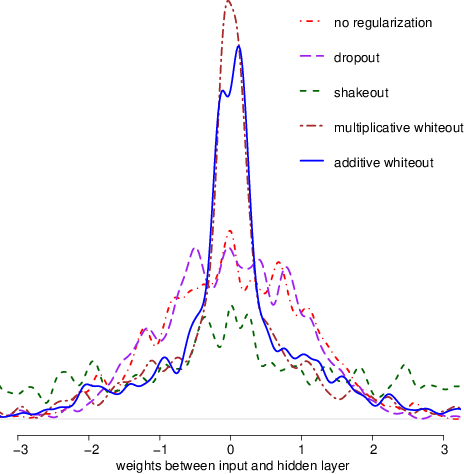
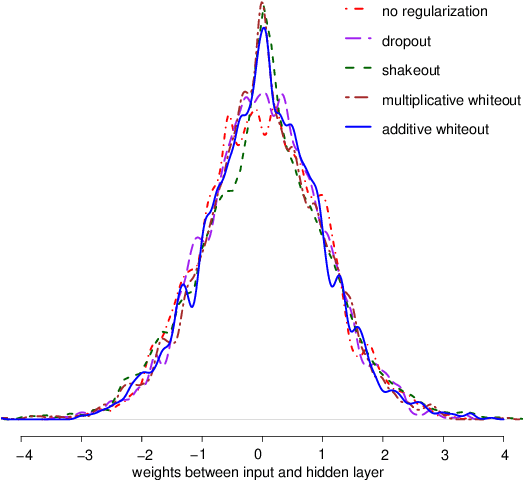
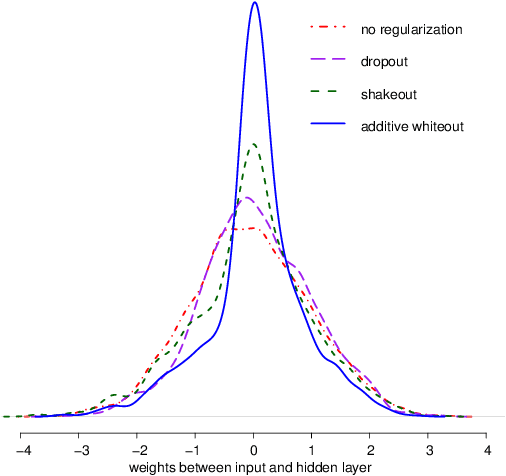
Abstract:Noise injection (NI) is an efficient technique to mitigate over-fitting in neural networks (NNs). The Bernoulli NI procedure as implemented in dropout and shakeout has connections with $l_1$ and $l_2$ regularization for the NN model parameters. We propose whiteout, a family NI regularization techniques (NIRT) through injecting adaptive Gaussian noises during the training of NNs. Whiteout is the first NIRT than imposes a broad range of the $l_{\gamma}$ sparsity regularization $(\gamma\in(0,2))$ without having to involving the $l_2$ regularization. Whiteout can also be extended to offer regularizations similar to the adaptive lasso and group lasso. We establish the regularization effect of whiteout in the framework of generalized linear models with closed-form penalty terms and show that whiteout stabilizes the training of NNs with decreased sensitivity to small perturbations in the input. We establish that the noise-perturbed empirical loss function (pelf) with whiteout converges almost surely to the ideal loss function (ilf), and the minimizer of the pelf is consistent for the minimizer of the ilf. We derive the tail bound on the pelf to establish the practical feasibility in its minimization. The superiority of whiteout over the Bernoulli NIRTs, dropout and shakeout, in learning NNs with relatively small-sized training sets and non-inferiority in large-sized training sets is demonstrated in both simulated and real-life data sets. This work represents the first in-depth theoretical, methodological, and practical examination of the regularization effects of both additive and multiplicative Gaussian NI in deep NNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge