Introducing Milabench: Benchmarking Accelerators for AI

AI workloads, particularly those driven by deep learning, are introducing novel usage patterns to high-performance computing (HPC) systems that are not comprehensively captured by standard HPC benchmarks. As one of the largest academic research centers dedicated to deep learning, Mila identified the need to develop a custom benchmarking suite to address the diverse requirements of its community, which consists of over 1,000 researchers. This report introduces Milabench, the resulting benchmarking suite. Its design was informed by an extensive literature review encompassing 867 papers, as well as surveys conducted with Mila researchers. This rigorous process led to the selection of 26 primary benchmarks tailored for procurement evaluations, alongside 16 optional benchmarks for in-depth analysis. We detail the design methodology, the structure of the benchmarking suite, and provide performance evaluations using GPUs from NVIDIA, AMD, and Intel. The Milabench suite is open source and can be accessed at github.com/mila-iqia/milabench.

LMEMs for post-hoc analysis of HPO Benchmarking

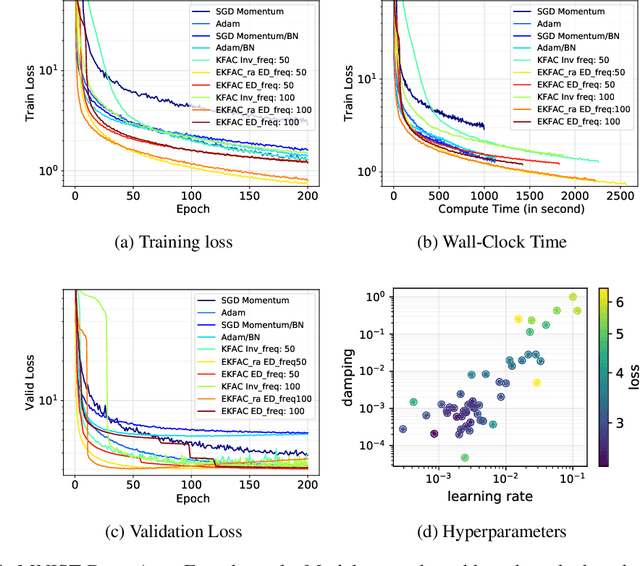
The importance of tuning hyperparameters in Machine Learning (ML) and Deep Learning (DL) is established through empirical research and applications, evident from the increase in new hyperparameter optimization (HPO) algorithms and benchmarks steadily added by the community. However, current benchmarking practices using averaged performance across many datasets may obscure key differences between HPO methods, especially for pairwise comparisons. In this work, we apply Linear Mixed-Effect Models-based (LMEMs) significance testing for post-hoc analysis of HPO benchmarking runs. LMEMs allow flexible and expressive modeling on the entire experiment data, including information such as benchmark meta-features, offering deeper insights than current analysis practices. We demonstrate this through a case study on the PriorBand paper's experiment data to find insights not reported in the original work.

Accounting for Variance in Machine Learning Benchmarks

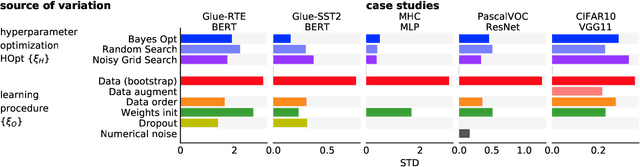
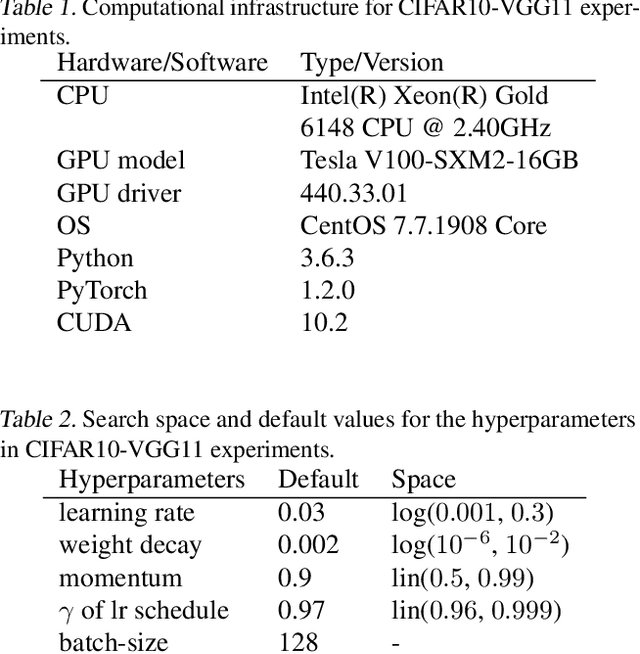
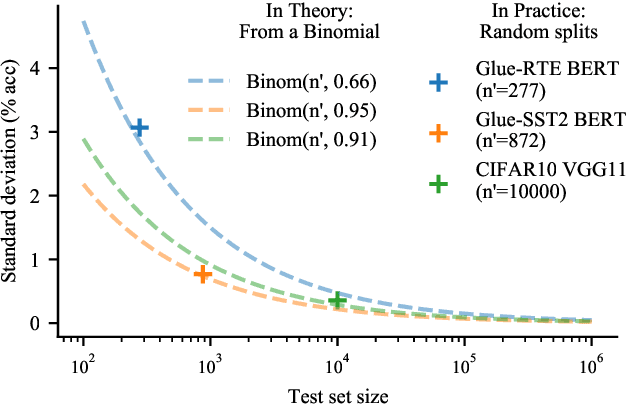
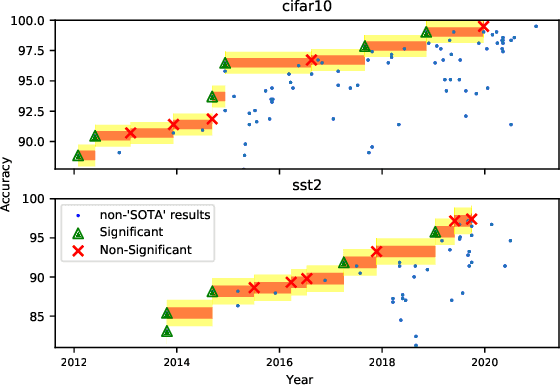
Strong empirical evidence that one machine-learning algorithm A outperforms another one B ideally calls for multiple trials optimizing the learning pipeline over sources of variation such as data sampling, data augmentation, parameter initialization, and hyperparameters choices. This is prohibitively expensive, and corners are cut to reach conclusions. We model the whole benchmarking process, revealing that variance due to data sampling, parameter initialization and hyperparameter choice impact markedly the results. We analyze the predominant comparison methods used today in the light of this variance. We show a counter-intuitive result that adding more sources of variation to an imperfect estimator approaches better the ideal estimator at a 51 times reduction in compute cost. Building on these results, we study the error rate of detecting improvements, on five different deep-learning tasks/architectures. This study leads us to propose recommendations for performance comparisons.

Fast Approximate Natural Gradient Descent in a Kronecker-factored Eigenbasis

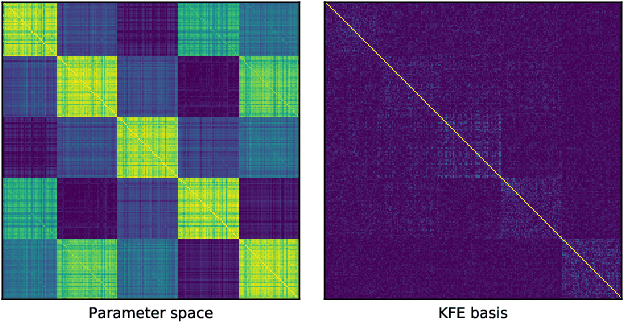
Optimization algorithms that leverage gradient covariance information, such as variants of natural gradient descent (Amari, 1998), offer the prospect of yielding more effective descent directions. For models with many parameters, the covariance matrix they are based on becomes gigantic, making them inapplicable in their original form. This has motivated research into both simple diagonal approximations and more sophisticated factored approximations such as KFAC (Heskes, 2000; Martens & Grosse, 2015; Grosse & Martens, 2016). In the present work we draw inspiration from both to propose a novel approximation that is provably better than KFAC and amendable to cheap partial updates. It consists in tracking a diagonal variance, not in parameter coordinates, but in a Kronecker-factored eigenbasis, in which the diagonal approximation is likely to be more effective. Experiments show improvements over KFAC in optimization speed for several deep network architectures.

Exact gradient updates in time independent of output size for the spherical loss family

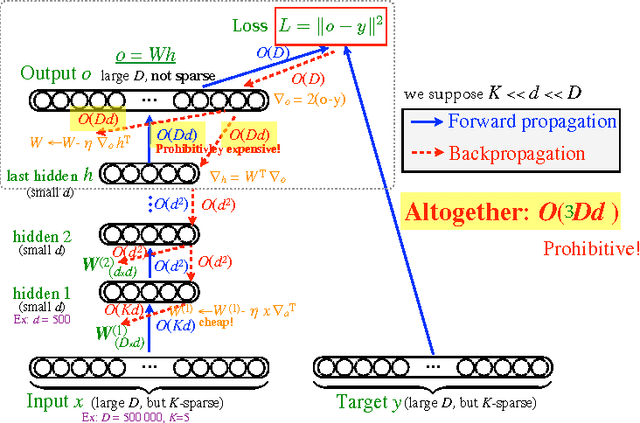
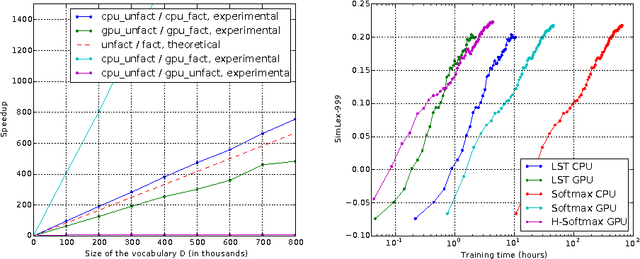
An important class of problems involves training deep neural networks with sparse prediction targets of very high dimension D. These occur naturally in e.g. neural language models or the learning of word-embeddings, often posed as predicting the probability of next words among a vocabulary of size D (e.g. 200,000). Computing the equally large, but typically non-sparse D-dimensional output vector from a last hidden layer of reasonable dimension d (e.g. 500) incurs a prohibitive O(Dd) computational cost for each example, as does updating the $D \times d$ output weight matrix and computing the gradient needed for backpropagation to previous layers. While efficient handling of large sparse network inputs is trivial, the case of large sparse targets is not, and has thus so far been sidestepped with approximate alternatives such as hierarchical softmax or sampling-based approximations during training. In this work we develop an original algorithmic approach which, for a family of loss functions that includes squared error and spherical softmax, can compute the exact loss, gradient update for the output weights, and gradient for backpropagation, all in $O(d^{2})$ per example instead of $O(Dd)$, remarkably without ever computing the D-dimensional output. The proposed algorithm yields a speedup of up to $D/4d$ i.e. two orders of magnitude for typical sizes, for that critical part of the computations that often dominates the training time in this kind of network architecture.

Theano: A Python framework for fast computation of mathematical expressions

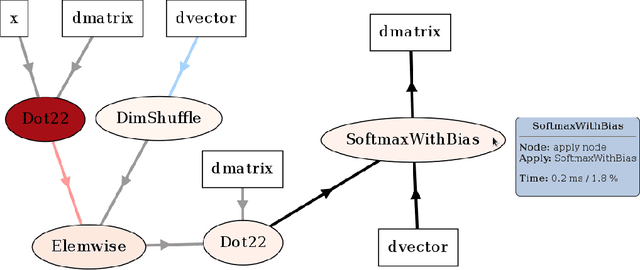
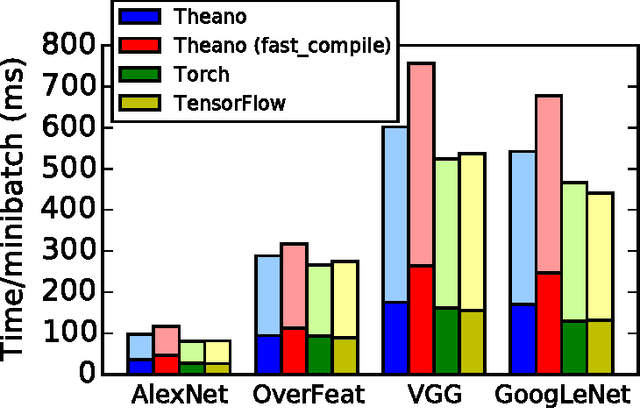
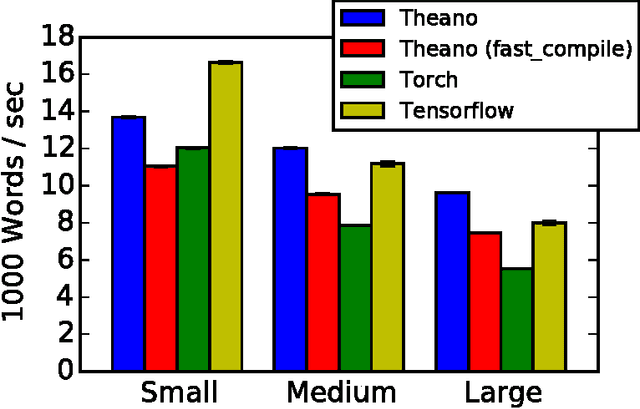
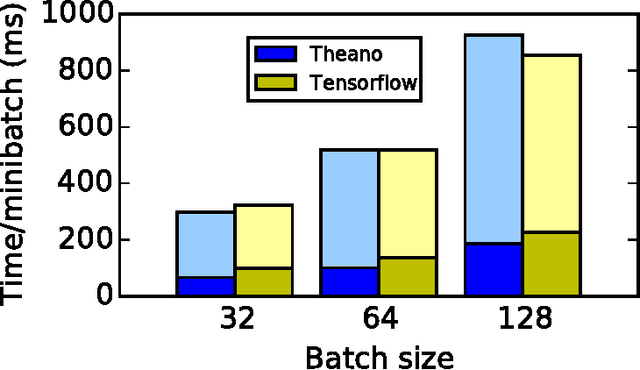
Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.

Dropout as data augmentation

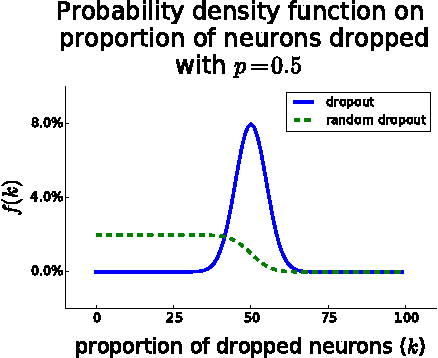
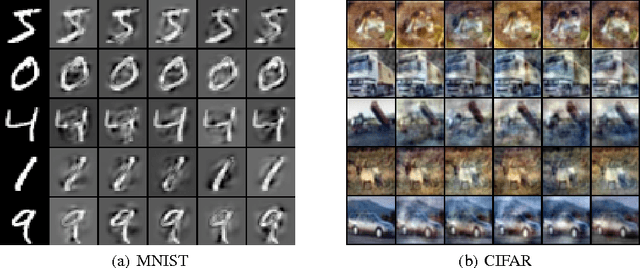
Dropout is typically interpreted as bagging a large number of models sharing parameters. We show that using dropout in a network can also be interpreted as a kind of data augmentation in the input space without domain knowledge. We present an approach to projecting the dropout noise within a network back into the input space, thereby generating augmented versions of the training data, and we show that training a deterministic network on the augmented samples yields similar results. Finally, we propose a new dropout noise scheme based on our observations and show that it improves dropout results without adding significant computational cost.

Efficient Exact Gradient Update for training Deep Networks with Very Large Sparse Targets

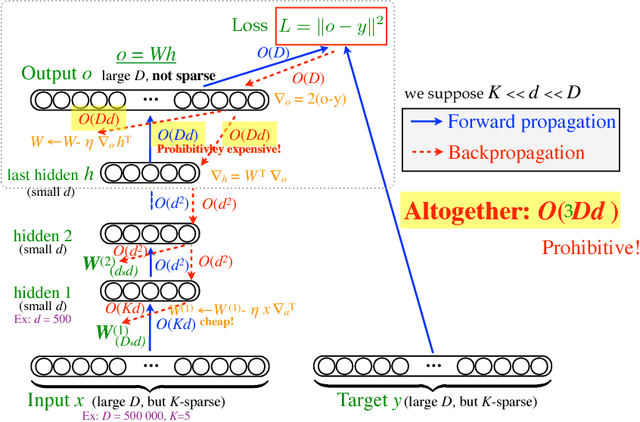
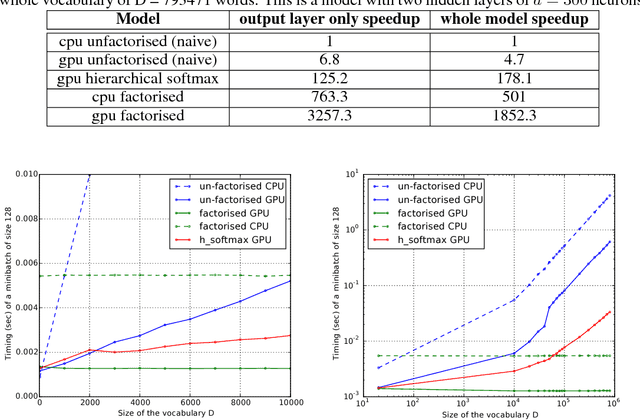
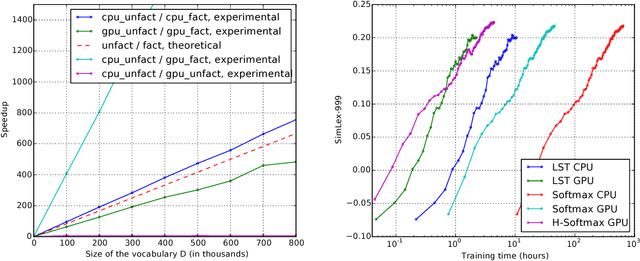
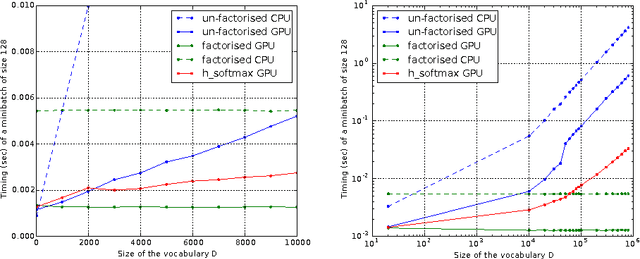
An important class of problems involves training deep neural networks with sparse prediction targets of very high dimension D. These occur naturally in e.g. neural language models or the learning of word-embeddings, often posed as predicting the probability of next words among a vocabulary of size D (e.g. 200 000). Computing the equally large, but typically non-sparse D-dimensional output vector from a last hidden layer of reasonable dimension d (e.g. 500) incurs a prohibitive O(Dd) computational cost for each example, as does updating the D x d output weight matrix and computing the gradient needed for backpropagation to previous layers. While efficient handling of large sparse network inputs is trivial, the case of large sparse targets is not, and has thus so far been sidestepped with approximate alternatives such as hierarchical softmax or sampling-based approximations during training. In this work we develop an original algorithmic approach which, for a family of loss functions that includes squared error and spherical softmax, can compute the exact loss, gradient update for the output weights, and gradient for backpropagation, all in O(d^2) per example instead of O(Dd), remarkably without ever computing the D-dimensional output. The proposed algorithm yields a speedup of D/4d , i.e. two orders of magnitude for typical sizes, for that critical part of the computations that often dominates the training time in this kind of network architecture.

EmoNets: Multimodal deep learning approaches for emotion recognition in video

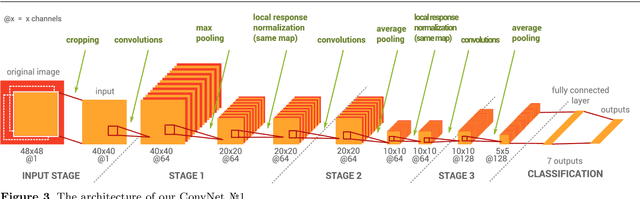
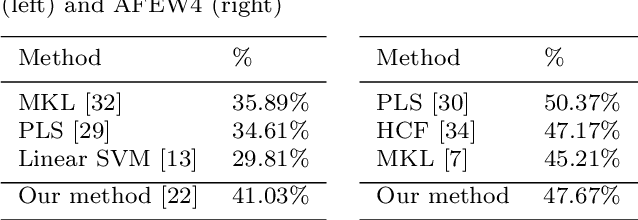
The task of the emotion recognition in the wild (EmotiW) Challenge is to assign one of seven emotions to short video clips extracted from Hollywood style movies. The videos depict acted-out emotions under realistic conditions with a large degree of variation in attributes such as pose and illumination, making it worthwhile to explore approaches which consider combinations of features from multiple modalities for label assignment. In this paper we present our approach to learning several specialist models using deep learning techniques, each focusing on one modality. Among these are a convolutional neural network, focusing on capturing visual information in detected faces, a deep belief net focusing on the representation of the audio stream, a K-Means based "bag-of-mouths" model, which extracts visual features around the mouth region and a relational autoencoder, which addresses spatio-temporal aspects of videos. We explore multiple methods for the combination of cues from these modalities into one common classifier. This achieves a considerably greater accuracy than predictions from our strongest single-modality classifier. Our method was the winning submission in the 2013 EmotiW challenge and achieved a test set accuracy of 47.67% on the 2014 dataset.