Versatile Cataract Fundus Image Restoration Model Utilizing Unpaired Cataract and High-quality Images

Cataract is one of the most common blinding eye diseases and can be treated by surgery. However, because cataract patients may also suffer from other blinding eye diseases, ophthalmologists must diagnose them before surgery. The cloudy lens of cataract patients forms a hazy degeneration in the fundus images, making it challenging to observe the patient's fundus vessels, which brings difficulties to the diagnosis process. To address this issue, this paper establishes a new cataract image restoration method named Catintell. It contains a cataract image synthesizing model, Catintell-Syn, and a restoration model, Catintell-Res. Catintell-Syn uses GAN architecture with fully unsupervised data to generate paired cataract-like images with realistic style and texture rather than the conventional Gaussian degradation algorithm. Meanwhile, Catintell-Res is an image restoration network that can improve the quality of real cataract fundus images using the knowledge learned from synthetic cataract images. Extensive experiments show that Catintell-Res outperforms other cataract image restoration methods in PSNR with 39.03 and SSIM with 0.9476. Furthermore, the universal restoration ability that Catintell-Res gained from unpaired cataract images can process cataract images from various datasets. We hope the models can help ophthalmologists identify other blinding eye diseases of cataract patients and inspire more medical image restoration methods in the future.

GPT-4o System Card

GPT-4o is an autoregressive omni model that accepts as input any combination of text, audio, image, and video, and generates any combination of text, audio, and image outputs. It's trained end-to-end across text, vision, and audio, meaning all inputs and outputs are processed by the same neural network. GPT-4o can respond to audio inputs in as little as 232 milliseconds, with an average of 320 milliseconds, which is similar to human response time in conversation. It matches GPT-4 Turbo performance on text in English and code, with significant improvement on text in non-English languages, while also being much faster and 50\% cheaper in the API. GPT-4o is especially better at vision and audio understanding compared to existing models. In line with our commitment to building AI safely and consistent with our voluntary commitments to the White House, we are sharing the GPT-4o System Card, which includes our Preparedness Framework evaluations. In this System Card, we provide a detailed look at GPT-4o's capabilities, limitations, and safety evaluations across multiple categories, focusing on speech-to-speech while also evaluating text and image capabilities, and measures we've implemented to ensure the model is safe and aligned. We also include third-party assessments on dangerous capabilities, as well as discussion of potential societal impacts of GPT-4o's text and vision capabilities.

Vitruvion: A Generative Model of Parametric CAD Sketches

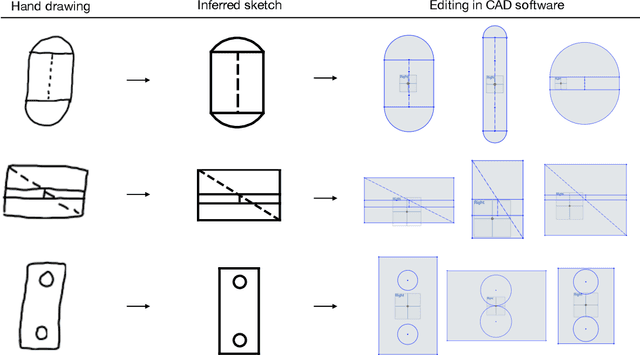
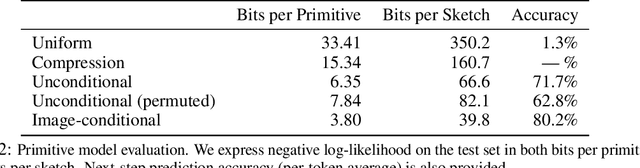
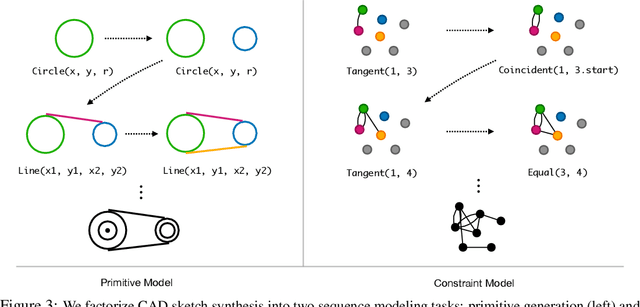
Parametric computer-aided design (CAD) tools are the predominant way that engineers specify physical structures, from bicycle pedals to airplanes to printed circuit boards. The key characteristic of parametric CAD is that design intent is encoded not only via geometric primitives, but also by parameterized constraints between the elements. This relational specification can be viewed as the construction of a constraint program, allowing edits to coherently propagate to other parts of the design. Machine learning offers the intriguing possibility of accelerating the design process via generative modeling of these structures, enabling new tools such as autocompletion, constraint inference, and conditional synthesis. In this work, we present such an approach to generative modeling of parametric CAD sketches, which constitute the basic computational building blocks of modern mechanical design. Our model, trained on real-world designs from the SketchGraphs dataset, autoregressively synthesizes sketches as sequences of primitives, with initial coordinates, and constraints that reference back to the sampled primitives. As samples from the model match the constraint graph representation used in standard CAD software, they may be directly imported, solved, and edited according to downstream design tasks. In addition, we condition the model on various contexts, including partial sketches (primers) and images of hand-drawn sketches. Evaluation of the proposed approach demonstrates its ability to synthesize realistic CAD sketches and its potential to aid the mechanical design workflow.

Autobahn: Automorphism-based Graph Neural Nets

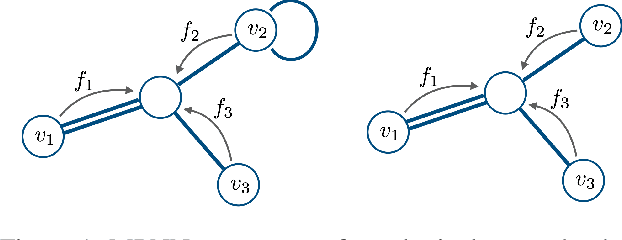
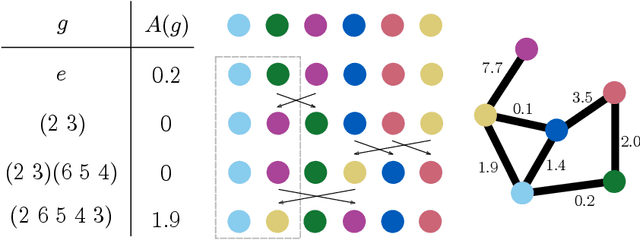
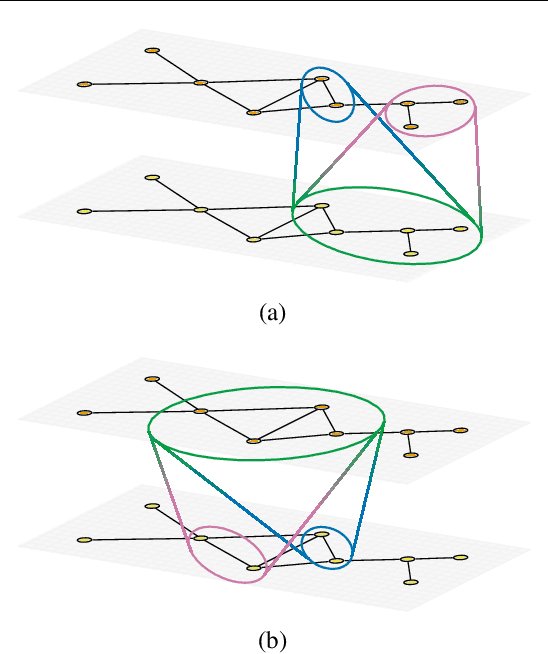
We introduce Automorphism-based graph neural networks (Autobahn), a new family of graph neural networks. In an Autobahn, we decompose the graph into a collection of subgraphs and applying local convolutions that are equivariant to each subgraph's automorphism group. Specific choices of local neighborhoods and subgraphs recover existing architectures such as message passing neural networks. However, our formalism also encompasses novel architectures: as an example, we introduce a graph neural network that decomposes the graph into paths and cycles. The resulting convolutions reflect the natural way that parts of the graph can transform, preserving the intuitive meaning of convolution without sacrificing global permutation equivariance. We validate our approach by applying Autobahn to molecular graphs, where it achieves state-of-the-art results.

SketchGraphs: A Large-Scale Dataset for Modeling Relational Geometry in Computer-Aided Design

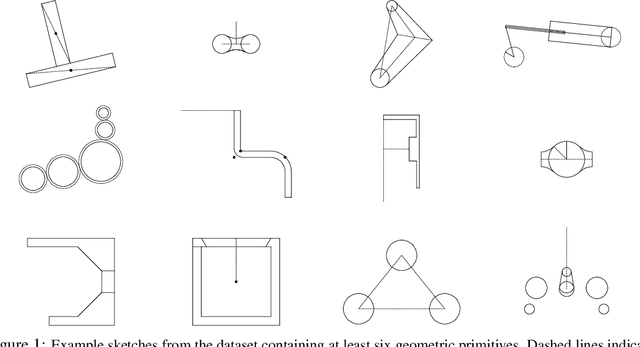
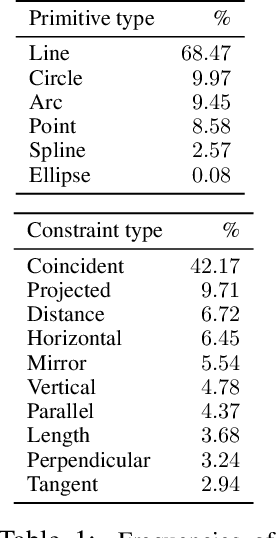
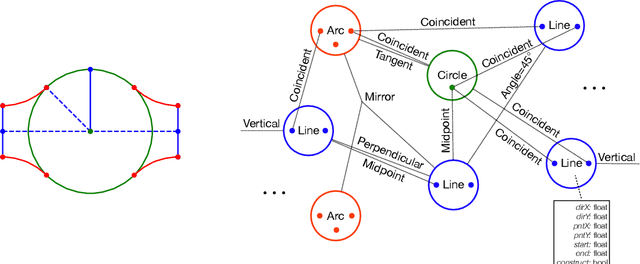
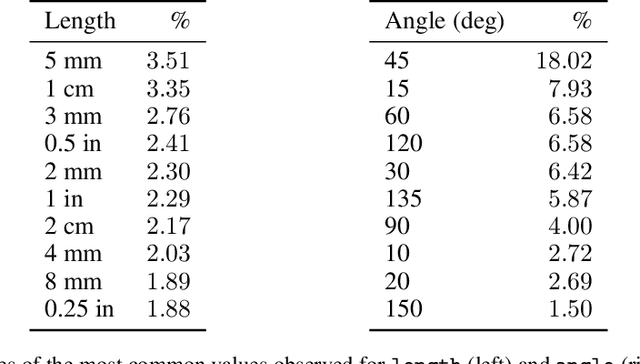
Parametric computer-aided design (CAD) is the dominant paradigm in mechanical engineering for physical design. Distinguished by relational geometry, parametric CAD models begin as two-dimensional sketches consisting of geometric primitives (e.g., line segments, arcs) and explicit constraints between them (e.g., coincidence, perpendicularity) that form the basis for three-dimensional construction operations. Training machine learning models to reason about and synthesize parametric CAD designs has the potential to reduce design time and enable new design workflows. Additionally, parametric CAD designs can be viewed as instances of constraint programming and they offer a well-scoped test bed for exploring ideas in program synthesis and induction. To facilitate this research, we introduce SketchGraphs, a collection of 15 million sketches extracted from real-world CAD models coupled with an open-source data processing pipeline. Each sketch is represented as a geometric constraint graph where edges denote designer-imposed geometric relationships between primitives, the nodes of the graph. We demonstrate and establish benchmarks for two use cases of the dataset: generative modeling of sketches and conditional generation of likely constraints given unconstrained geometry.

Error bounds in estimating the out-of-sample prediction error using leave-one-out cross validation in high-dimensions

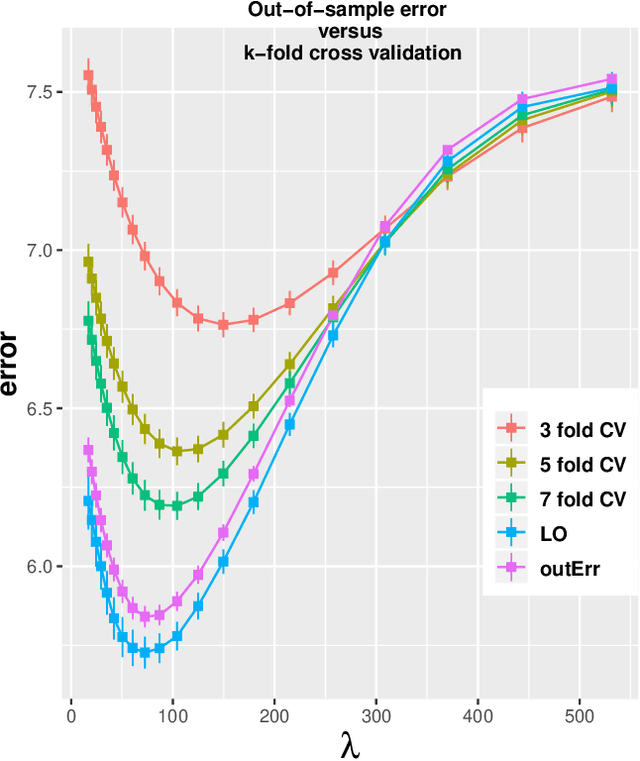
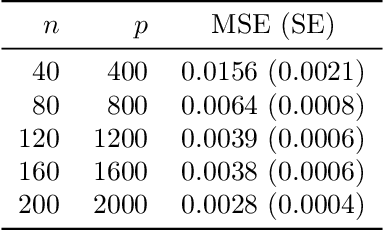
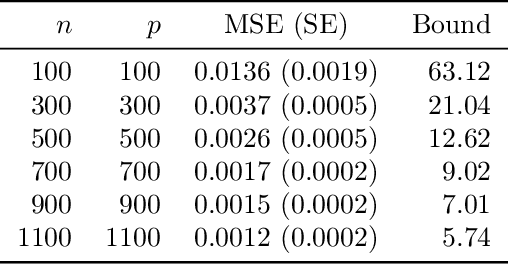
We study the problem of out-of-sample risk estimation in the high dimensional regime where both the sample size $n$ and number of features $p$ are large, and $n/p$ can be less than one. Extensive empirical evidence confirms the accuracy of leave-one-out cross validation (LO) for out-of-sample risk estimation. Yet, a unifying theoretical evaluation of the accuracy of LO in high-dimensional problems has remained an open problem. This paper aims to fill this gap for penalized regression in the generalized linear family. With minor assumptions about the data generating process, and without any sparsity assumptions on the regression coefficients, our theoretical analysis obtains finite sample upper bounds on the expected squared error of LO in estimating the out-of-sample error. Our bounds show that the error goes to zero as $n,p \rightarrow \infty$, even when the dimension $p$ of the feature vectors is comparable with or greater than the sample size $n$. One technical advantage of the theory is that it can be used to clarify and connect some results from the recent literature on scalable approximate LO.

Discrete Object Generation with Reversible Inductive Construction

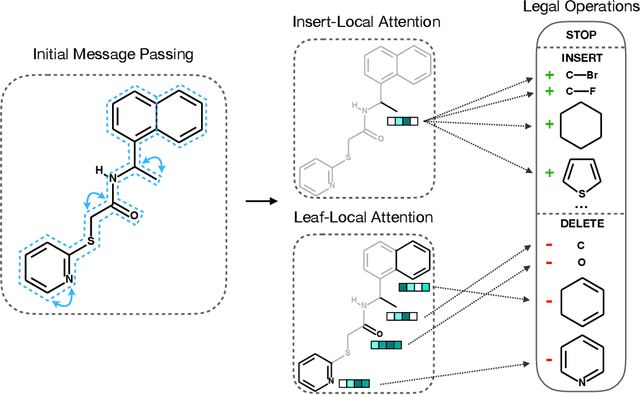
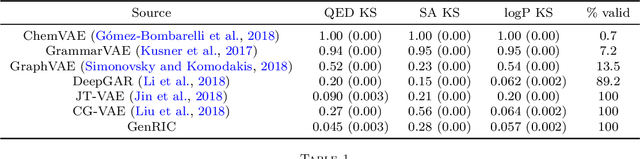
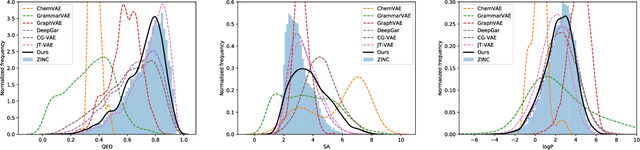
The success of generative modeling in continuous domains has led to a surge of interest in generating discrete data such as molecules, source code, and graphs. However, construction histories for these discrete objects are typically not unique and so generative models must reason about intractably large spaces in order to learn. Additionally, structured discrete domains are often characterized by strict constraints on what constitutes a valid object and generative models must respect these requirements in order to produce useful novel samples. Here, we present a generative model for discrete objects employing a Markov chain where transitions are restricted to a set of local operations that preserve validity. Building off of generative interpretations of denoising autoencoders, the Markov chain alternates between producing 1) a sequence of corrupted objects that are valid but not from the data distribution, and 2) a learned reconstruction distribution that attempts to fix the corruptions while also preserving validity. This approach constrains the generative model to only produce valid objects, requires the learner to only discover local modifications to the objects, and avoids marginalization over an unknown and potentially large space of construction histories. We evaluate the proposed approach on two highly structured discrete domains, molecules and Laman graphs, and find that it compares favorably to alternative methods at capturing distributional statistics for a host of semantically relevant metrics.

Approximate Leave-One-Out for Fast Parameter Tuning in High Dimensions

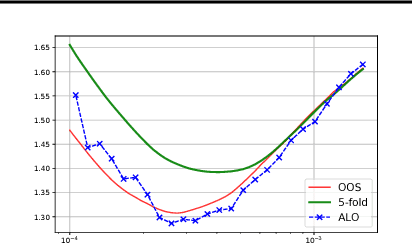
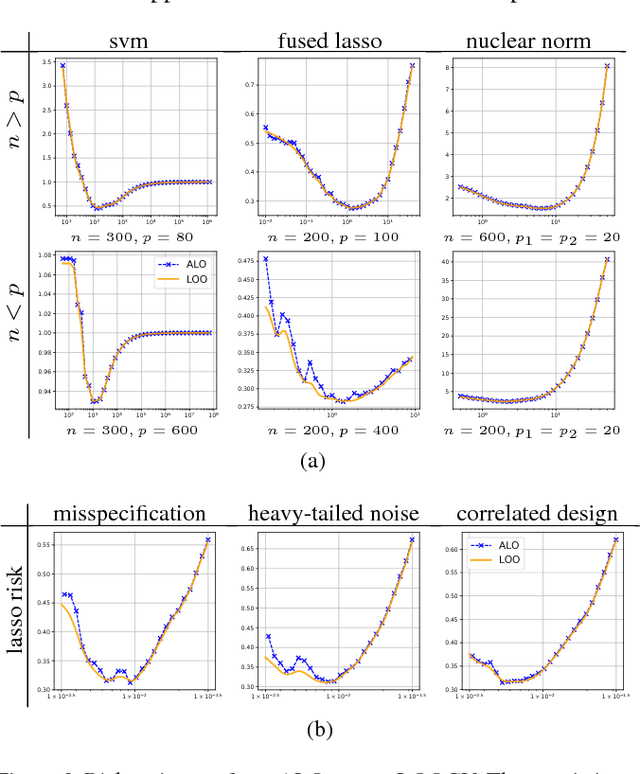
Consider the following class of learning schemes: $$\hat{\boldsymbol{\beta}} := \arg\min_{\boldsymbol{\beta}}\;\sum_{j=1}^n \ell(\boldsymbol{x}_j^\top\boldsymbol{\beta}; y_j) + \lambda R(\boldsymbol{\beta}),\qquad\qquad (1) $$ where $\boldsymbol{x}_i \in \mathbb{R}^p$ and $y_i \in \mathbb{R}$ denote the $i^{\text{th}}$ feature and response variable respectively. Let $\ell$ and $R$ be the loss function and regularizer, $\boldsymbol{\beta}$ denote the unknown weights, and $\lambda$ be a regularization parameter. Finding the optimal choice of $\lambda$ is a challenging problem in high-dimensional regimes where both $n$ and $p$ are large. We propose two frameworks to obtain a computationally efficient approximation ALO of the leave-one-out cross validation (LOOCV) risk for nonsmooth losses and regularizers. Our two frameworks are based on the primal and dual formulations of (1). We prove the equivalence of the two approaches under smoothness conditions. This equivalence enables us to justify the accuracy of both methods under such conditions. We use our approaches to obtain a risk estimate for several standard problems, including generalized LASSO, nuclear norm regularization, and support vector machines. We empirically demonstrate the effectiveness of our results for non-differentiable cases.

Empirical Risk Minimization and Stochastic Gradient Descent for Relational Data

Empirical risk minimization is the principal tool for prediction problems, but its extension to relational data remains unsolved. We solve this problem using recent advances in graph sampling theory. We (i) define an empirical risk for relational data and (ii) obtain stochastic gradients for this risk that are automatically unbiased. The key ingredient is to consider the method by which data is sampled from a graph as an explicit component of model design. Theoretical results establish that the choice of sampling scheme is critical. By integrating fast implementations of graph sampling schemes with standard automatic differentiation tools, we are able to solve the risk minimization in a plug-and-play fashion even on large datasets. We demonstrate empirically that relational ERM models achieve state-of-the-art results on semi-supervised node classification tasks. The experiments also confirm the importance of the choice of sampling scheme.

Compressibility and Generalization in Large-Scale Deep Learning

Modern neural networks are highly overparameterized, with capacity to substantially overfit to training data. Nevertheless, these networks often generalize well in practice. It has also been observed that trained networks can often be "compressed" to much smaller representations. The purpose of this paper is to connect these two empirical observations. Our main technical result is a generalization bound for compressed networks based on the compressed size. Combined with off-the-shelf compression algorithms, the bound leads to state of the art generalization guarantees; in particular, we provide the first non-vacuous generalization guarantees for realistic architectures applied to the ImageNet classification problem. As additional evidence connecting compression and generalization, we show that compressibility of models that tend to overfit is limited: We establish an absolute limit on expected compressibility as a function of expected generalization error, where the expectations are over the random choice of training examples. The bounds are complemented by empirical results that show an increase in overfitting implies an increase in the number of bits required to describe a trained network.