SketchGraphs: A Large-Scale Dataset for Modeling Relational Geometry in Computer-Aided Design

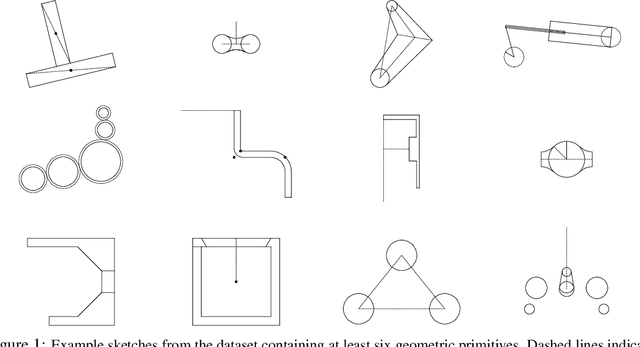
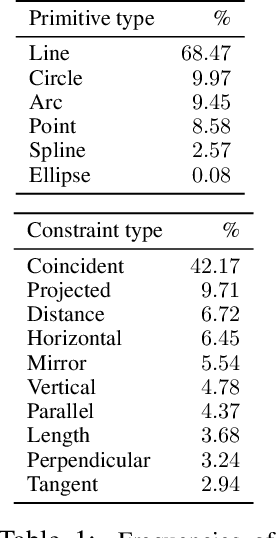
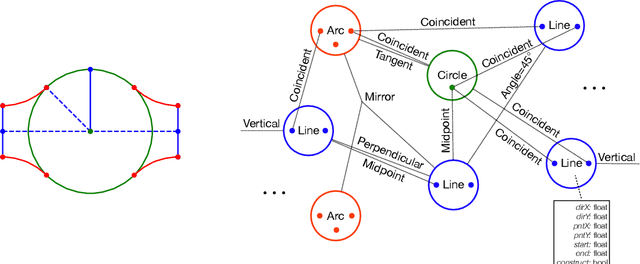
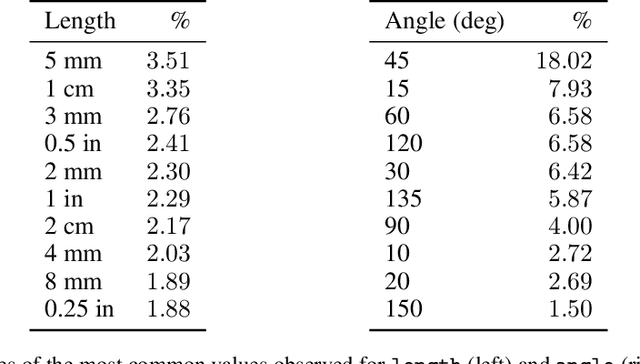
Parametric computer-aided design (CAD) is the dominant paradigm in mechanical engineering for physical design. Distinguished by relational geometry, parametric CAD models begin as two-dimensional sketches consisting of geometric primitives (e.g., line segments, arcs) and explicit constraints between them (e.g., coincidence, perpendicularity) that form the basis for three-dimensional construction operations. Training machine learning models to reason about and synthesize parametric CAD designs has the potential to reduce design time and enable new design workflows. Additionally, parametric CAD designs can be viewed as instances of constraint programming and they offer a well-scoped test bed for exploring ideas in program synthesis and induction. To facilitate this research, we introduce SketchGraphs, a collection of 15 million sketches extracted from real-world CAD models coupled with an open-source data processing pipeline. Each sketch is represented as a geometric constraint graph where edges denote designer-imposed geometric relationships between primitives, the nodes of the graph. We demonstrate and establish benchmarks for two use cases of the dataset: generative modeling of sketches and conditional generation of likely constraints given unconstrained geometry.

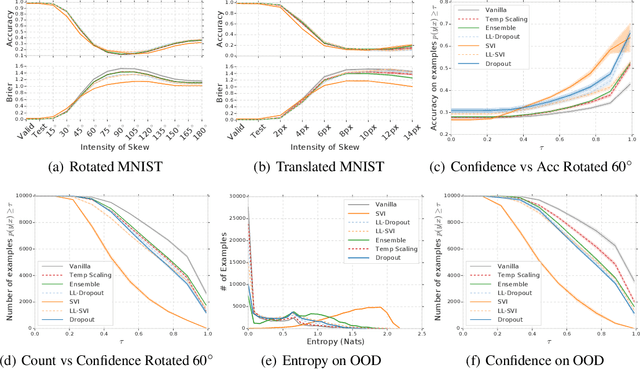
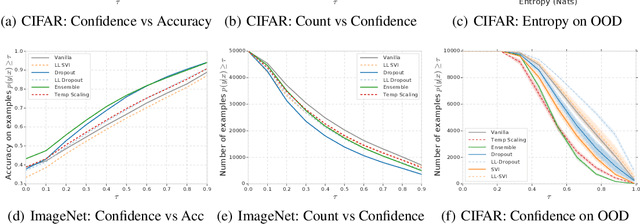
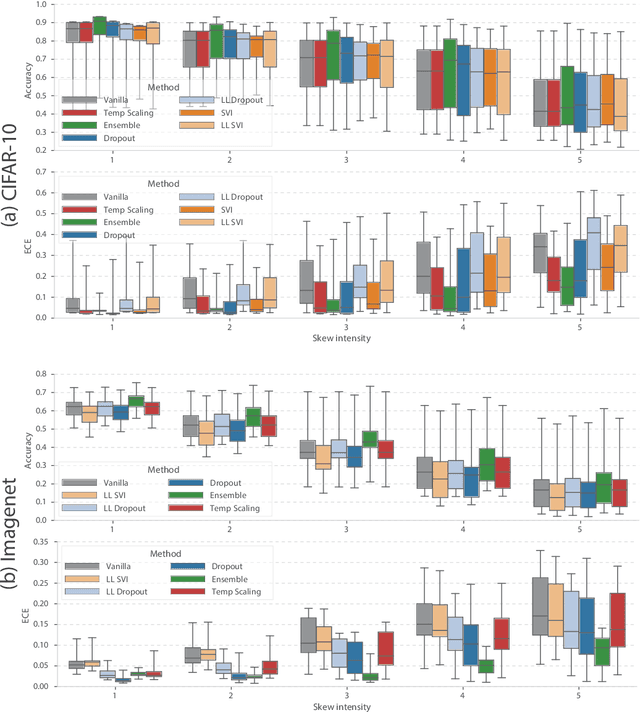
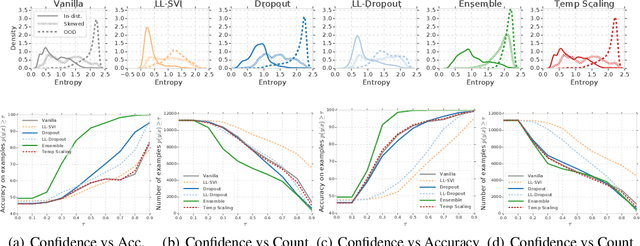
Can You Trust Your Model's Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift

Modern machine learning methods including deep learning have achieved great success in predictive accuracy for supervised learning tasks, but may still fall short in giving useful estimates of their predictive {\em uncertainty}. Quantifying uncertainty is especially critical in real-world settings, which often involve input distributions that are shifted from the training distribution due to a variety of factors including sample bias and non-stationarity. In such settings, well calibrated uncertainty estimates convey information about when a model's output should (or should not) be trusted. Many probabilistic deep learning methods, including Bayesian-and non-Bayesian methods, have been proposed in the literature for quantifying predictive uncertainty, but to our knowledge there has not previously been a rigorous large-scale empirical comparison of these methods under dataset shift. We present a large-scale benchmark of existing state-of-the-art methods on classification problems and investigate the effect of dataset shift on accuracy and calibration. We find that traditional post-hoc calibration does indeed fall short, as do several other previous methods. However, some methods that marginalize over models give surprisingly strong results across a broad spectrum of tasks.

DPPNet: Approximating Determinantal Point Processes with Deep Networks

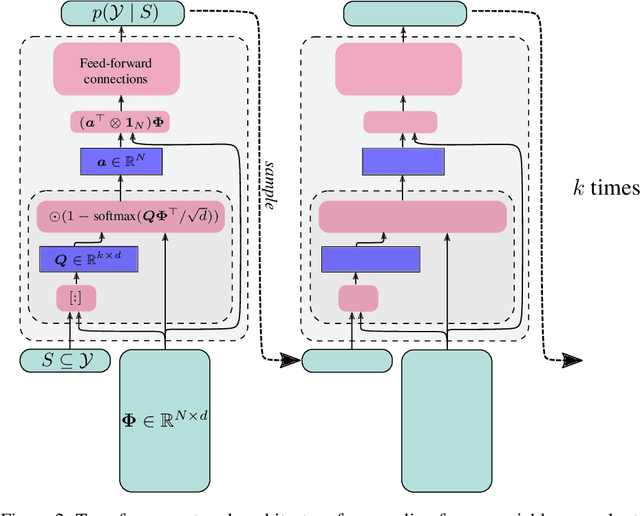
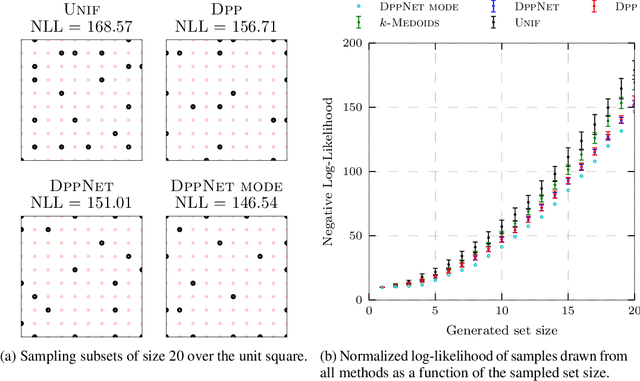
Determinantal Point Processes (DPPs) provide an elegant and versatile way to sample sets of items that balance the point-wise quality with the set-wise diversity of selected items. For this reason, they have gained prominence in many machine learning applications that rely on subset selection. However, sampling from a DPP over a ground set of size $N$ is a costly operation, requiring in general an $O(N^3)$ preprocessing cost and an $O(Nk^3)$ sampling cost for subsets of size $k$. We approach this problem by introducing DPPNets: generative deep models that produce DPP-like samples for arbitrary ground sets. We develop an inhibitive attention mechanism based on transformer networks that captures a notion of dissimilarity between feature vectors. We show theoretically that such an approximation is sensible as it maintains the guarantees of inhibition or dissimilarity that makes DPPs so powerful and unique. Empirically, we demonstrate that samples from our model receive high likelihood under the more expensive DPP alternative.

Estimating the Spectral Density of Large Implicit Matrices

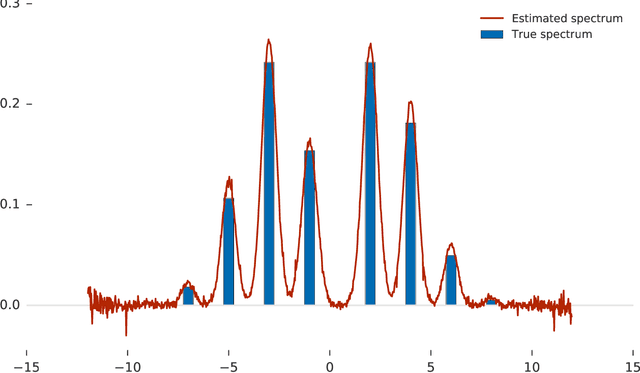
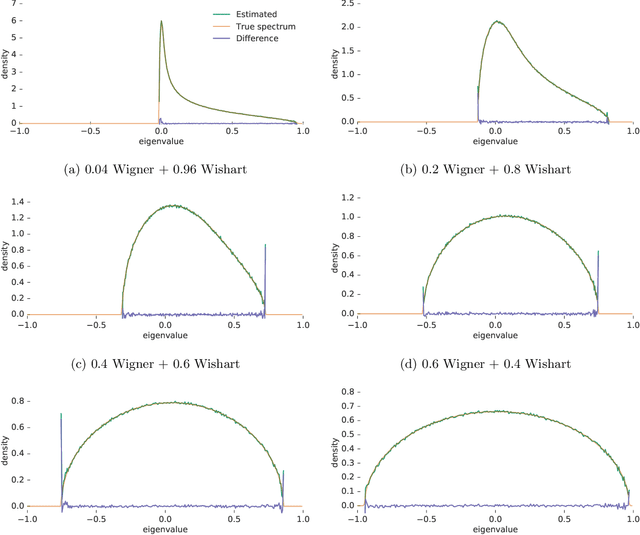
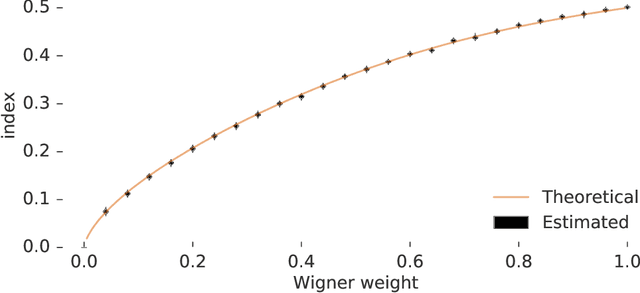
Many important problems are characterized by the eigenvalues of a large matrix. For example, the difficulty of many optimization problems, such as those arising from the fitting of large models in statistics and machine learning, can be investigated via the spectrum of the Hessian of the empirical loss function. Network data can be understood via the eigenstructure of a graph Laplacian matrix using spectral graph theory. Quantum simulations and other many-body problems are often characterized via the eigenvalues of the solution space, as are various dynamic systems. However, naive eigenvalue estimation is computationally expensive even when the matrix can be represented; in many of these situations the matrix is so large as to only be available implicitly via products with vectors. Even worse, one may only have noisy estimates of such matrix vector products. In this work, we combine several different techniques for randomized estimation and show that it is possible to construct unbiased estimators to answer a broad class of questions about the spectra of such implicit matrices, even in the presence of noise. We validate these methods on large-scale problems in which graph theory and random matrix theory provide ground truth.