Multilook Coherent Imaging: Theoretical Guarantees and Algorithms

Multilook coherent imaging is a widely used technique in applications such as digital holography, ultrasound imaging, and synthetic aperture radar. A central challenge in these systems is the presence of multiplicative noise, commonly known as speckle, which degrades image quality. Despite the widespread use of coherent imaging systems, their theoretical foundations remain relatively underexplored. In this paper, we study both the theoretical and algorithmic aspects of likelihood-based approaches for multilook coherent imaging, providing a rigorous framework for analysis and method development. Our theoretical contributions include establishing the first theoretical upper bound on the Mean Squared Error (MSE) of the maximum likelihood estimator under the deep image prior hypothesis. Our results capture the dependence of MSE on the number of parameters in the deep image prior, the number of looks, the signal dimension, and the number of measurements per look. On the algorithmic side, we employ projected gradient descent (PGD) as an efficient method for computing the maximum likelihood solution. Furthermore, we introduce two key ideas to enhance the practical performance of PGD. First, we incorporate the Newton-Schulz algorithm to compute matrix inverses within the PGD iterations, significantly reducing computational complexity. Second, we develop a bagging strategy to mitigate projection errors introduced during PGD updates. We demonstrate that combining these techniques with PGD yields state-of-the-art performance. Our code is available at https://github.com/Computational-Imaging-RU/Bagged-DIP-Speckle.

Certified Data Removal Under High-dimensional Settings

Machine unlearning focuses on the computationally efficient removal of specific training data from trained models, ensuring that the influence of forgotten data is effectively eliminated without the need for full retraining. Despite advances in low-dimensional settings, where the number of parameters \( p \) is much smaller than the sample size \( n \), extending similar theoretical guarantees to high-dimensional regimes remains challenging. We propose an unlearning algorithm that starts from the original model parameters and performs a theory-guided sequence of Newton steps \( T \in \{ 1,2\}\). After this update, carefully scaled isotropic Laplacian noise is added to the estimate to ensure that any (potential) residual influence of forget data is completely removed. We show that when both \( n, p \to \infty \) with a fixed ratio \( n/p \), significant theoretical and computational obstacles arise due to the interplay between the complexity of the model and the finite signal-to-noise ratio. Finally, we show that, unlike in low-dimensional settings, a single Newton step is insufficient for effective unlearning in high-dimensional problems -- however, two steps are enough to achieve the desired certifiebility. We provide numerical experiments to support the certifiability and accuracy claims of this approach.

Phase Transitions in Phase-Only Compressed Sensing

The goal of phase-only compressed sensing is to recover a structured signal $\mathbf{x}$ from the phases $\mathbf{z} = {\rm sign}(\mathbf{\Phi}\mathbf{x})$ under some complex-valued sensing matrix $\mathbf{\Phi}$. Exact reconstruction of the signal's direction is possible: we can reformulate it as a linear compressed sensing problem and use basis pursuit (i.e., constrained norm minimization). For $\mathbf{\Phi}$ with i.i.d. complex-valued Gaussian entries, this paper shows that the phase transition is approximately located at the statistical dimension of the descent cone of a signal-dependent norm. Leveraging this insight, we derive asymptotically precise formulas for the phase transition locations in phase-only sensing of both sparse signals and low-rank matrices. Our results prove that the minimum number of measurements required for exact recovery is smaller for phase-only measurements than for traditional linear compressed sensing. For instance, in recovering a 1-sparse signal with sufficiently large dimension, phase-only compressed sensing requires approximately 68% of the measurements needed for linear compressed sensing. This result disproves earlier conjecture suggesting that the two phase transitions coincide. Our proof hinges on the Gaussian min-max theorem and the key observation that, up to a signal-dependent orthogonal transformation, the sensing matrix in the reformulated problem behaves as a nearly Gaussian matrix.

Comprehensive Examination of Unrolled Networks for Linear Inverse Problems

Unrolled networks have become prevalent in various computer vision and imaging tasks. Although they have demonstrated remarkable efficacy in solving specific computer vision and computational imaging tasks, their adaptation to other applications presents considerable challenges. This is primarily due to the multitude of design decisions that practitioners working on new applications must navigate, each potentially affecting the network's overall performance. These decisions include selecting the optimization algorithm, defining the loss function, and determining the number of convolutional layers, among others. Compounding the issue, evaluating each design choice requires time-consuming simulations to train, fine-tune the neural network, and optimize for its performance. As a result, the process of exploring multiple options and identifying the optimal configuration becomes time-consuming and computationally demanding. The main objectives of this paper are (1) to unify some ideas and methodologies used in unrolled networks to reduce the number of design choices a user has to make, and (2) to report a comprehensive ablation study to discuss the impact of each of the choices involved in designing unrolled networks and present practical recommendations based on our findings. We anticipate that this study will help scientists and engineers design unrolled networks for their applications and diagnose problems within their networks efficiently.

Is speckle noise more challenging to mitigate than additive noise?

We study the problem of estimating a function in the presence of both speckle and additive noises. Although additive noise has been thoroughly explored in nonparametric estimation, speckle noise, prevalent in applications such as synthetic aperture radar, ultrasound imaging, and digital holography, has not received as much attention. Consequently, there is a lack of theoretical investigations into the fundamental limits of mitigating the speckle noise. This paper is the first step in filling this gap. Our focus is on investigating the minimax estimation error for estimating a $\beta$-H\"older continuous function and determining the rate of the minimax risk. Specifically, if $n$ represents the number of data points, $f$ denotes the underlying function to be estimated, and $\hat{\nu}_n$ is an estimate of $f$, then $\inf_{\hat{\nu}_n} \sup_f \mathbb{E}_f\| \hat{\nu}_n - f \|^2_2$ decays at the rate $n^{-\frac{2\beta}{2\beta+1}}$. Interestingly, this rate is identical to the one achieved for mitigating additive noise when the noise's variance is $\Theta(1)$. To validate the accuracy of our minimax upper bounds, we implement the minimax optimal algorithms on simulated data and employ Monte Carlo simulations to characterize their exact risk. Our simulations closely mirror the expected behaviors in decay rate as per our theory.

Bagged Deep Image Prior for Recovering Images in the Presence of Speckle Noise

We investigate both the theoretical and algorithmic aspects of likelihood-based methods for recovering a complex-valued signal from multiple sets of measurements, referred to as looks, affected by speckle (multiplicative) noise. Our theoretical contributions include establishing the first existing theoretical upper bound on the Mean Squared Error (MSE) of the maximum likelihood estimator under the deep image prior hypothesis. Our theoretical results capture the dependence of MSE upon the number of parameters in the deep image prior, the number of looks, the signal dimension, and the number of measurements per look. On the algorithmic side, we introduce the concept of bagged Deep Image Priors (Bagged-DIP) and integrate them with projected gradient descent. Furthermore, we show how employing Newton-Schulz algorithm for calculating matrix inverses within the iterations of PGD reduces the computational complexity of the algorithm. We will show that this method achieves the state-of-the-art performance.

Theoretical Analysis of Leave-one-out Cross Validation for Non-differentiable Penalties under High-dimensional Settings

Despite a large and significant body of recent work focused on estimating the out-of-sample risk of regularized models in the high dimensional regime, a theoretical understanding of this problem for non-differentiable penalties such as generalized LASSO and nuclear norm is missing. In this paper we resolve this challenge. We study this problem in the proportional high dimensional regime where both the sample size n and number of features p are large, and n/p and the signal-to-noise ratio (per observation) remain finite. We provide finite sample upper bounds on the expected squared error of leave-one-out cross-validation (LO) in estimating the out-of-sample risk. The theoretical framework presented here provides a solid foundation for elucidating empirical findings that show the accuracy of LO.

Approximate Leave-one-out Cross Validation for Regression with $\ell_1$ Regularizers (extended version)

The out-of-sample error (OO) is the main quantity of interest in risk estimation and model selection. Leave-one-out cross validation (LO) offers a (nearly) distribution-free yet computationally demanding approach to estimate OO. Recent theoretical work showed that approximate leave-one-out cross validation (ALO) is a computationally efficient and statistically reliable estimate of LO (and OO) for generalized linear models with differentiable regularizers. For problems involving non-differentiable regularizers, despite significant empirical evidence, the theoretical understanding of ALO's error remains unknown. In this paper, we present a novel theory for a wide class of problems in the generalized linear model family with non-differentiable regularizers. We bound the error |ALO - LO| in terms of intuitive metrics such as the size of leave-i-out perturbations in active sets, sample size n, number of features p and regularization parameters. As a consequence, for the $\ell_1$-regularized problems, we show that |ALO - LO| goes to zero as p goes to infinity while n/p and SNR are fixed and bounded.

Impact of the Sensing Spectrum on Signal Recovery in Generalized Linear Models

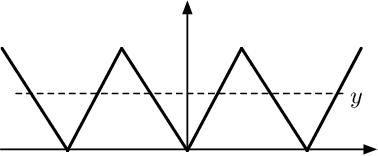
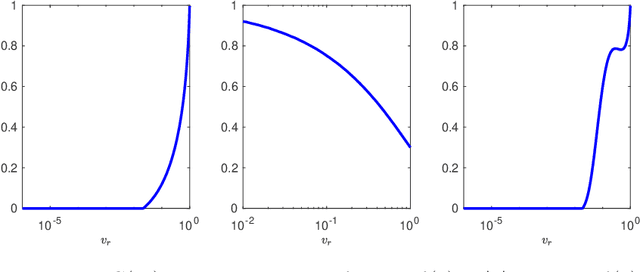
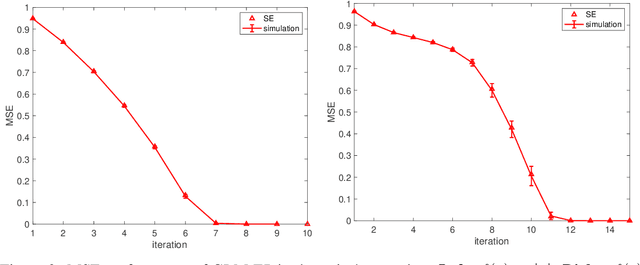
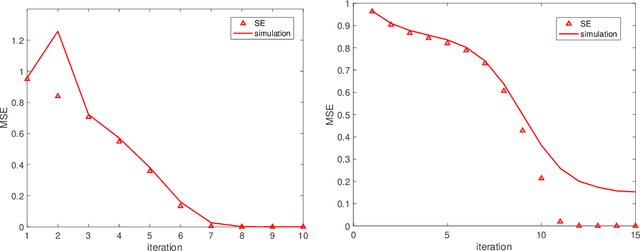
We consider a nonlinear inverse problem $\mathbf{y}= f(\mathbf{Ax})$, where observations $\mathbf{y} \in \mathbb{R}^m$ are the componentwise nonlinear transformation of $\mathbf{Ax} \in \mathbb{R}^m$, $\mathbf{x} \in \mathbb{R}^n$ is the signal of interest and $\mathbf{A}$ is a known linear mapping. By properly specifying the nonlinear processing function, this model can be particularized to many signal processing problems, including compressed sensing and phase retrieval. Our main goal in this paper is to understand the impact of sensing matrices, or more specifically the spectrum of sensing matrices, on the difficulty of recovering $\mathbf{x}$ from $\mathbf{y}$. Towards this goal, we study the performance of one of the most successful recovery methods, i.e. the expectation propagation algorithm (EP). We define a notion for the spikiness of the spectrum of $\mathbf{A}$ and show the importance of this measure in the performance of the EP. Whether the spikiness of the spectrum can hurt or help the recovery performance of EP depends on $f$. We define certain quantities based on the function $f$ that enables us to describe the impact of the spikiness of the spectrum on EP recovery. Based on our framework, we are able to show that for instance, in phase-retrieval problems, matrices with spikier spectrums are better for EP, while in 1-bit compressed sensing problems, less spiky (flatter) spectrums offer better recoveries. Our results unify and substantially generalize the existing results that compare sub-Gaussian and orthogonal matrices, and provide a platform toward designing optimal sensing systems.

Sharp Concentration Results for Heavy-Tailed Distributions

We obtain concentration and large deviation for the sums of independent and identically distributed random variables with heavy-tailed distributions. Our concentration results are concerned with random variables whose distributions satisfy $P(X>t) \leq {\rm e}^{- I(t)}$, where $I: \mathbb{R} \rightarrow \mathbb{R}$ is an increasing function and $I(t)/t \rightarrow \alpha \in [0, \infty)$ as $t \rightarrow \infty$. Our main theorem can not only recover some of the existing results, such as the concentration of the sum of subWeibull random variables, but it can also produce new results for the sum of random variables with heavier tails. We show that the concentration inequalities we obtain are sharp enough to offer large deviation results for the sums of independent random variables as well. Our analyses which are based on standard truncation arguments simplify, unify and generalize the existing results on the concentration and large deviation of heavy-tailed random variables.