A Single Architecture for Representing Invariance Under Any Space Group

Incorporating known symmetries in data into machine learning models has consistently improved predictive accuracy, robustness, and generalization. However, achieving exact invariance to specific symmetries typically requires designing bespoke architectures for each group of symmetries, limiting scalability and preventing knowledge transfer across related symmetries. In the case of the space groups, symmetries critical to modeling crystalline solids in materials science and condensed matter physics, this challenge is particularly salient as there are 230 such groups in three dimensions. In this work we present a new approach to such crystallographic symmetries by developing a single machine learning architecture that is capable of adapting its weights automatically to enforce invariance to any input space group. Our approach is based on constructing symmetry-adapted Fourier bases through an explicit characterization of constraints that group operations impose on Fourier coefficients. Encoding these constraints into a neural network layer enables weight sharing across different space groups, allowing the model to leverage structural similarities between groups and overcome data sparsity when limited measurements are available for specific groups. We demonstrate the effectiveness of this approach in achieving competitive performance on material property prediction tasks and performing zero-shot learning to generalize to unseen groups.

Local Learning Rules for Out-of-Equilibrium Physical Generative Models

We show that the out-of-equilibrium driving protocol of score-based generative models (SGMs) can be learned via a local learning rule. The gradient with respect to the parameters of the driving protocol are computed directly from force measurements or from observed system dynamics. As a demonstration, we implement an SGM in a network of driven, nonlinear, overdamped oscillators coupled to a thermal bath. We first apply it to the problem of sampling from a mixture of two Gaussians in 2D. Finally, we train a network of 10x10 oscillators to sample images of 0s and 1s from the MNIST dataset.

Space Group Equivariant Crystal Diffusion

Accelerating inverse design of crystalline materials with generative models has significant implications for a range of technologies. Unlike other atomic systems, 3D crystals are invariant to discrete groups of isometries called the space groups. Crucially, these space group symmetries are known to heavily influence materials properties. We propose SGEquiDiff, a crystal generative model which naturally handles space group constraints with space group invariant likelihoods. SGEquiDiff consists of an SE(3)-invariant, telescoping discrete sampler of crystal lattices; permutation-invariant, transformer-based autoregressive sampling of Wyckoff positions, elements, and numbers of symmetrically unique atoms; and space group equivariant diffusion of atomic coordinates. We show that space group equivariant vector fields automatically live in the tangent spaces of the Wyckoff positions. SGEquiDiff achieves state-of-the-art performance on standard benchmark datasets as assessed by quantitative proxy metrics and quantum mechanical calculations.

Diagonal Symmetrization of Neural Network Solvers for the Many-Electron Schrödinger Equation

Incorporating group symmetries into neural networks has been a cornerstone of success in many AI-for-science applications. Diagonal groups of isometries, which describe the invariance under a simultaneous movement of multiple objects, arise naturally in many-body quantum problems. Despite their importance, diagonal groups have received relatively little attention, as they lack a natural choice of invariant maps except in special cases. We study different ways of incorporating diagonal invariance in neural network ans\"atze trained via variational Monte Carlo methods, and consider specifically data augmentation, group averaging and canonicalization. We show that, contrary to standard ML setups, in-training symmetrization destabilizes training and can lead to worse performance. Our theoretical and numerical results indicate that this unexpected behavior may arise from a unique computational-statistical tradeoff not found in standard ML analyses of symmetrization. Meanwhile, we demonstrate that post hoc averaging is less sensitive to such tradeoffs and emerges as a simple, flexible and effective method for improving neural network solvers.

Graph Neural Networks Gone Hogwild

Message passing graph neural networks (GNNs) would appear to be powerful tools to learn distributed algorithms via gradient descent, but generate catastrophically incorrect predictions when nodes update asynchronously during inference. This failure under asynchrony effectively excludes these architectures from many potential applications, such as learning local communication policies between resource-constrained agents in, e.g., robotic swarms or sensor networks. In this work we explore why this failure occurs in common GNN architectures, and identify "implicitly-defined" GNNs as a class of architectures which is provably robust to partially asynchronous "hogwild" inference, adapting convergence guarantees from work in asynchronous and distributed optimization, e.g., Bertsekas (1982); Niu et al. (2011). We then propose a novel implicitly-defined GNN architecture, which we call an energy GNN. We show that this architecture outperforms other GNNs from this class on a variety of synthetic tasks inspired by multi-agent systems, and achieves competitive performance on real-world datasets.

Generative Marginalization Models

We introduce marginalization models (MaMs), a new family of generative models for high-dimensional discrete data. They offer scalable and flexible generative modeling with tractable likelihoods by explicitly modeling all induced marginal distributions. Marginalization models enable fast evaluation of arbitrary marginal probabilities with a single forward pass of the neural network, which overcomes a major limitation of methods with exact marginal inference, such as autoregressive models (ARMs). We propose scalable methods for learning the marginals, grounded in the concept of "marginalization self-consistency". Unlike previous methods, MaMs support scalable training of any-order generative models for high-dimensional problems under the setting of energy-based training, where the goal is to match the learned distribution to a given desired probability (specified by an unnormalized (log) probability function such as energy function or reward function). We demonstrate the effectiveness of the proposed model on a variety of discrete data distributions, including binary images, language, physical systems, and molecules, for maximum likelihood and energy-based training settings. MaMs achieve orders of magnitude speedup in evaluating the marginal probabilities on both settings. For energy-based training tasks, MaMs enable any-order generative modeling of high-dimensional problems beyond the capability of previous methods. Code is at https://github.com/PrincetonLIPS/MaM.

Representing and Learning Functions Invariant Under Crystallographic Groups

Crystallographic groups describe the symmetries of crystals and other repetitive structures encountered in nature and the sciences. These groups include the wallpaper and space groups. We derive linear and nonlinear representations of functions that are (1) smooth and (2) invariant under such a group. The linear representation generalizes the Fourier basis to crystallographically invariant basis functions. We show that such a basis exists for each crystallographic group, that it is orthonormal in the relevant $L_2$ space, and recover the standard Fourier basis as a special case for pure shift groups. The nonlinear representation embeds the orbit space of the group into a finite-dimensional Euclidean space. We show that such an embedding exists for every crystallographic group, and that it factors functions through a generalization of a manifold called an orbifold. We describe algorithms that, given a standardized description of the group, compute the Fourier basis and an embedding map. As examples, we construct crystallographically invariant neural networks, kernel machines, and Gaussian processes.

Neuromechanical Autoencoders: Learning to Couple Elastic and Neural Network Nonlinearity

Intelligent biological systems are characterized by their embodiment in a complex environment and the intimate interplay between their nervous systems and the nonlinear mechanical properties of their bodies. This coordination, in which the dynamics of the motor system co-evolved to reduce the computational burden on the brain, is referred to as ``mechanical intelligence'' or ``morphological computation''. In this work, we seek to develop machine learning analogs of this process, in which we jointly learn the morphology of complex nonlinear elastic solids along with a deep neural network to control it. By using a specialized differentiable simulator of elastic mechanics coupled to conventional deep learning architectures -- which we refer to as neuromechanical autoencoders -- we are able to learn to perform morphological computation via gradient descent. Key to our approach is the use of mechanical metamaterials -- cellular solids, in particular -- as the morphological substrate. Just as deep neural networks provide flexible and massively-parametric function approximators for perceptual and control tasks, cellular solid metamaterials are promising as a rich and learnable space for approximating a variety of actuation tasks. In this work we take advantage of these complementary computational concepts to co-design materials and neural network controls to achieve nonintuitive mechanical behavior. We demonstrate in simulation how it is possible to achieve translation, rotation, and shape matching, as well as a ``digital MNIST'' task. We additionally manufacture and evaluate one of the designs to verify its real-world behavior.

Meta-PDE: Learning to Solve PDEs Quickly Without a Mesh

Partial differential equations (PDEs) are often computationally challenging to solve, and in many settings many related PDEs must be be solved either at every timestep or for a variety of candidate boundary conditions, parameters, or geometric domains. We present a meta-learning based method which learns to rapidly solve problems from a distribution of related PDEs. We use meta-learning (MAML and LEAP) to identify initializations for a neural network representation of the PDE solution such that a residual of the PDE can be quickly minimized on a novel task. We apply our meta-solving approach to a nonlinear Poisson's equation, 1D Burgers' equation, and hyperelasticity equations with varying parameters, geometries, and boundary conditions. The resulting Meta-PDE method finds qualitatively accurate solutions to most problems within a few gradient steps; for the nonlinear Poisson and hyper-elasticity equation this results in an intermediate accuracy approximation up to an order of magnitude faster than a baseline finite element analysis (FEA) solver with equivalent accuracy. In comparison to other learned solvers and surrogate models, this meta-learning approach can be trained without supervision from expensive ground-truth data, does not require a mesh, and can even be used when the geometry and topology varies between tasks.

Multi-fidelity Monte Carlo: a pseudo-marginal approach

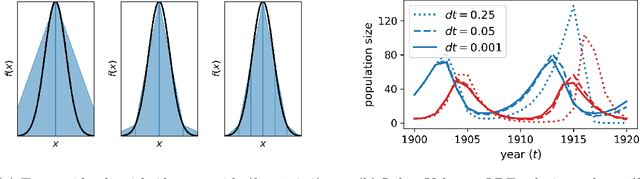
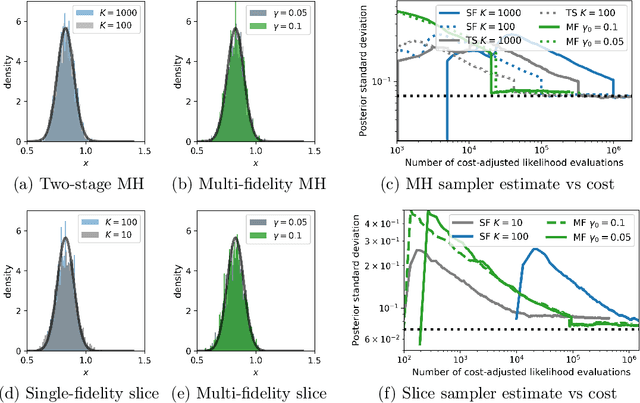
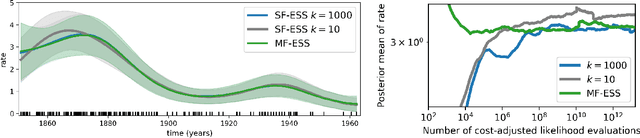
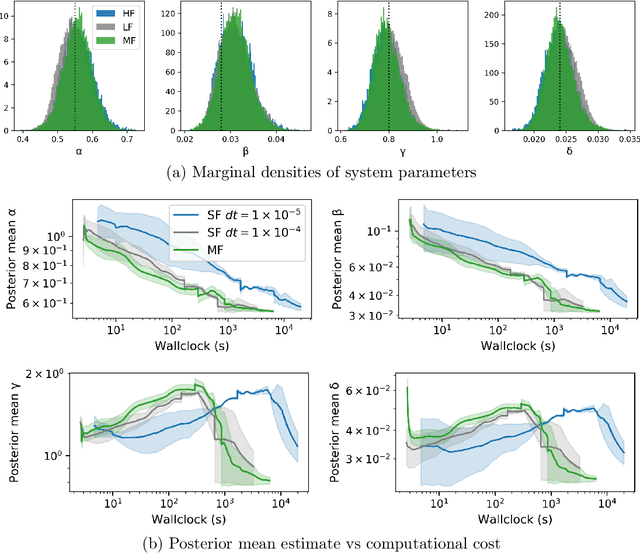
Markov chain Monte Carlo (MCMC) is an established approach for uncertainty quantification and propagation in scientific applications. A key challenge in applying MCMC to scientific domains is computation: the target density of interest is often a function of expensive computations, such as a high-fidelity physical simulation, an intractable integral, or a slowly-converging iterative algorithm. Thus, using an MCMC algorithms with an expensive target density becomes impractical, as these expensive computations need to be evaluated at each iteration of the algorithm. In practice, these computations often approximated via a cheaper, low-fidelity computation, leading to bias in the resulting target density. Multi-fidelity MCMC algorithms combine models of varying fidelities in order to obtain an approximate target density with lower computational cost. In this paper, we describe a class of asymptotically exact multi-fidelity MCMC algorithms for the setting where a sequence of models of increasing fidelity can be computed that approximates the expensive target density of interest. We take a pseudo-marginal MCMC approach for multi-fidelity inference that utilizes a cheaper, randomized-fidelity unbiased estimator of the target fidelity constructed via random truncation of a telescoping series of the low-fidelity sequence of models. Finally, we discuss and evaluate the proposed multi-fidelity MCMC approach on several applications, including log-Gaussian Cox process modeling, Bayesian ODE system identification, PDE-constrained optimization, and Gaussian process regression parameter inference.