EigenVI: score-based variational inference with orthogonal function expansions

We develop EigenVI, an eigenvalue-based approach for black-box variational inference (BBVI). EigenVI constructs its variational approximations from orthogonal function expansions. For distributions over $\mathbb{R}^D$, the lowest order term in these expansions provides a Gaussian variational approximation, while higher-order terms provide a systematic way to model non-Gaussianity. These approximations are flexible enough to model complex distributions (multimodal, asymmetric), but they are simple enough that one can calculate their low-order moments and draw samples from them. EigenVI can also model other types of random variables (e.g., nonnegative, bounded) by constructing variational approximations from different families of orthogonal functions. Within these families, EigenVI computes the variational approximation that best matches the score function of the target distribution by minimizing a stochastic estimate of the Fisher divergence. Notably, this optimization reduces to solving a minimum eigenvalue problem, so that EigenVI effectively sidesteps the iterative gradient-based optimizations that are required for many other BBVI algorithms. (Gradient-based methods can be sensitive to learning rates, termination criteria, and other tunable hyperparameters.) We use EigenVI to approximate a variety of target distributions, including a benchmark suite of Bayesian models from posteriordb. On these distributions, we find that EigenVI is more accurate than existing methods for Gaussian BBVI.

Estimating the Causal Effects of T Cell Receptors

A central question in human immunology is how a patient's repertoire of T cells impacts disease. Here, we introduce a method to infer the causal effects of T cell receptor (TCR) sequences on patient outcomes using observational TCR repertoire sequencing data and clinical outcomes data. Our approach corrects for unobserved confounders, such as a patient's environment and life history, by using the patient's immature, pre-selection TCR repertoire. The pre-selection repertoire can be estimated from nonproductive TCR data, which is widely available. It is generated by a randomized mutational process, V(D)J recombination, which provides a natural experiment. We show formally how to use the pre-selection repertoire to draw causal inferences, and develop a scalable neural-network estimator for our identification formula. Our method produces an estimate of the effect of interventions that add a specific TCR sequence to patient repertoires. As a demonstration, we use it to analyze the effects of TCRs on COVID-19 severity, uncovering potentially therapeutic TCRs that are (1) observed in patients, (2) bind SARS-CoV-2 antigens in vitro and (3) have strong positive effects on clinical outcomes.

Hypothesis Testing the Circuit Hypothesis in LLMs

Large language models (LLMs) demonstrate surprising capabilities, but we do not understand how they are implemented. One hypothesis suggests that these capabilities are primarily executed by small subnetworks within the LLM, known as circuits. But how can we evaluate this hypothesis? In this paper, we formalize a set of criteria that a circuit is hypothesized to meet and develop a suite of hypothesis tests to evaluate how well circuits satisfy them. The criteria focus on the extent to which the LLM's behavior is preserved, the degree of localization of this behavior, and whether the circuit is minimal. We apply these tests to six circuits described in the research literature. We find that synthetic circuits -- circuits that are hard-coded in the model -- align with the idealized properties. Circuits discovered in Transformer models satisfy the criteria to varying degrees. To facilitate future empirical studies of circuits, we created the \textit{circuitry} package, a wrapper around the \textit{TransformerLens} library, which abstracts away lower-level manipulations of hooks and activations. The software is available at \url{https://github.com/blei-lab/circuitry}.

Estimating Wage Disparities Using Foundation Models

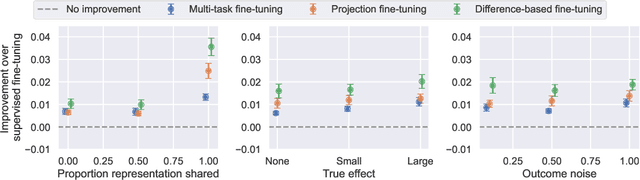
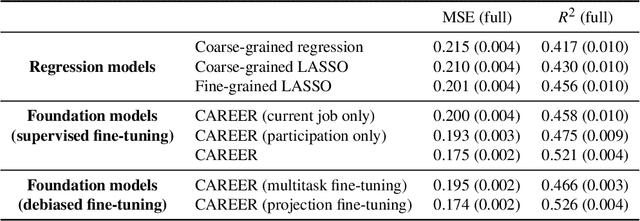
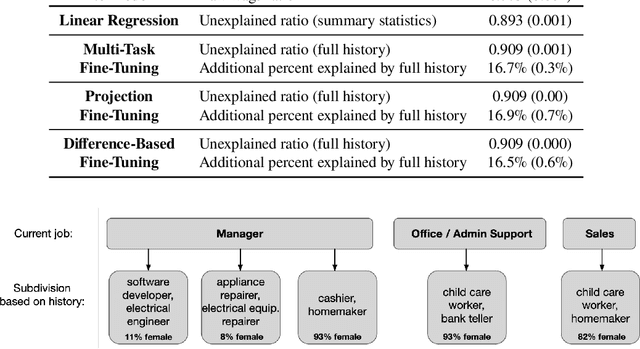
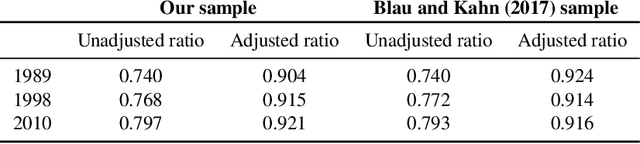
One thread of empirical work in social science focuses on decomposing group differences in outcomes into unexplained components and components explained by observable factors. In this paper, we study gender wage decompositions, which require estimating the portion of the gender wage gap explained by career histories of workers. Classical methods for decomposing the wage gap employ simple predictive models of wages which condition on a small set of simple summaries of labor history. The problem is that these predictive models cannot take advantage of the full complexity of a worker's history, and the resulting decompositions thus suffer from omitted variable bias (OVB), where covariates that are correlated with both gender and wages are not included in the model. Here we explore an alternative methodology for wage gap decomposition that employs powerful foundation models, such as large language models, as the predictive engine. Foundation models excel at making accurate predictions from complex, high-dimensional inputs. We use a custom-built foundation model, designed to predict wages from full labor histories, to decompose the gender wage gap. We prove that the way such models are usually trained might still lead to OVB, but develop fine-tuning algorithms that empirically mitigate this issue. Our model captures a richer representation of career history than simple models and predicts wages more accurately. In detail, we first provide a novel set of conditions under which an estimator of the wage gap based on a fine-tuned foundation model is $\sqrt{n}$-consistent. Building on the theory, we then propose methods for fine-tuning foundation models that minimize OVB. Using data from the Panel Study of Income Dynamics, we find that history explains more of the gender wage gap than standard econometric models can measure, and we identify elements of history that are important for reducing OVB.

Batch and match: black-box variational inference with a score-based divergence

Most leading implementations of black-box variational inference (BBVI) are based on optimizing a stochastic evidence lower bound (ELBO). But such approaches to BBVI often converge slowly due to the high variance of their gradient estimates. In this work, we propose batch and match (BaM), an alternative approach to BBVI based on a score-based divergence. Notably, this score-based divergence can be optimized by a closed-form proximal update for Gaussian variational families with full covariance matrices. We analyze the convergence of BaM when the target distribution is Gaussian, and we prove that in the limit of infinite batch size the variational parameter updates converge exponentially quickly to the target mean and covariance. We also evaluate the performance of BaM on Gaussian and non-Gaussian target distributions that arise from posterior inference in hierarchical and deep generative models. In these experiments, we find that BaM typically converges in fewer (and sometimes significantly fewer) gradient evaluations than leading implementations of BBVI based on ELBO maximization.

Hierarchical Causal Models

Scientists often want to learn about cause and effect from hierarchical data, collected from subunits nested inside units. Consider students in schools, cells in patients, or cities in states. In such settings, unit-level variables (e.g. each school's budget) may affect subunit-level variables (e.g. the test scores of each student in each school) and vice versa. To address causal questions with hierarchical data, we propose hierarchical causal models, which extend structural causal models and causal graphical models by adding inner plates. We develop a general graphical identification technique for hierarchical causal models that extends do-calculus. We find many situations in which hierarchical data can enable causal identification even when it would be impossible with non-hierarchical data, that is, if we had only unit-level summaries of subunit-level variables (e.g. the school's average test score, rather than each student's score). We develop estimation techniques for hierarchical causal models, using methods including hierarchical Bayesian models. We illustrate our results in simulation and via a reanalysis of the classic "eight schools" study.

Revisiting Topic-Guided Language Models

A recent line of work in natural language processing has aimed to combine language models and topic models. These topic-guided language models augment neural language models with topic models, unsupervised learning methods that can discover document-level patterns of word use. This paper compares the effectiveness of these methods in a standardized setting. We study four topic-guided language models and two baselines, evaluating the held-out predictive performance of each model on four corpora. Surprisingly, we find that none of these methods outperform a standard LSTM language model baseline, and most fail to learn good topics. Further, we train a probe of the neural language model that shows that the baseline's hidden states already encode topic information. We make public all code used for this study.

A Computational Approach to Style in American Poetry

We develop a quantitative method to assess the style of American poems and to visualize a collection of poems in relation to one another. Qualitative poetry criticism helped guide our development of metrics that analyze various orthographic, syntactic, and phonemic features. These features are used to discover comprehensive stylistic information from a poem's multi-layered latent structure, and to compute distances between poems in this space. Visualizations provide ready access to the analytical components. We demonstrate our method on several collections of poetry, showing that it better delineates poetry style than the traditional word-occurrence features that are used in typical text analysis algorithms. Our method has potential applications to academic research of texts, to research of the intuitive personal response to poetry, and to making recommendations to readers based on their favorite poems.

Evaluating the Moral Beliefs Encoded in LLMs

This paper presents a case study on the design, administration, post-processing, and evaluation of surveys on large language models (LLMs). It comprises two components: (1) A statistical method for eliciting beliefs encoded in LLMs. We introduce statistical measures and evaluation metrics that quantify the probability of an LLM "making a choice", the associated uncertainty, and the consistency of that choice. (2) We apply this method to study what moral beliefs are encoded in different LLMs, especially in ambiguous cases where the right choice is not obvious. We design a large-scale survey comprising 680 high-ambiguity moral scenarios (e.g., "Should I tell a white lie?") and 687 low-ambiguity moral scenarios (e.g., "Should I stop for a pedestrian on the road?"). Each scenario includes a description, two possible actions, and auxiliary labels indicating violated rules (e.g., "do not kill"). We administer the survey to 28 open- and closed-source LLMs. We find that (a) in unambiguous scenarios, most models "choose" actions that align with commonsense. In ambiguous cases, most models express uncertainty. (b) Some models are uncertain about choosing the commonsense action because their responses are sensitive to the question-wording. (c) Some models reflect clear preferences in ambiguous scenarios. Specifically, closed-source models tend to agree with each other.

Amortized Variational Inference: When and Why?

Amortized variational inference (A-VI) is a method for approximating the intractable posterior distributions that arise in probabilistic models. The defining feature of A-VI is that it learns a global inference function that maps each observation to its local latent variable's approximate posterior. This stands in contrast to the more classical factorized (or mean-field) variational inference (F-VI), which directly learns the parameters of the approximating distribution for each latent variable. In deep generative models, A-VI is used as a computational trick to speed up inference for local latent variables. In this paper, we study A-VI as a general alternative to F-VI for approximate posterior inference. A-VI cannot produce an approximation with a lower Kullback-Leibler divergence than F-VI's optimal solution, because the amortized family is a subset of the factorized family. Thus a central theoretical problem is to characterize when A-VI still attains F-VI's optimal solution. We derive conditions on both the model and the inference function under which A-VI can theoretically achieve F-VI's optimum. We show that for a broad class of hierarchical models, including deep generative models, it is possible to close the gap between A-VI and F-VI. Further, for an even broader class of models, we establish when and how to expand the domain of the inference function to make amortization a feasible strategy. Finally, we prove that for certain models -- including hidden Markov models and Gaussian processes -- A-VI cannot match F-VI's solution, no matter how expressive the inference function is. We also study A-VI empirically. On several examples, we corroborate our theoretical results and investigate the performance of A-VI when varying the complexity of the inference function. When the gap between A-VI and F-VI can be closed, we find that the required complexity of the function need not scale with the number of observations, and that A-VI often converges faster than F-VI.