Fully Dynamic Adversarially Robust Correlation Clustering in Polylogarithmic Update Time

We study the dynamic correlation clustering problem with $\textit{adaptive}$ edge label flips. In correlation clustering, we are given a $n$-vertex complete graph whose edges are labeled either $(+)$ or $(-)$, and the goal is to minimize the total number of $(+)$ edges between clusters and the number of $(-)$ edges within clusters. We consider the dynamic setting with adversarial robustness, in which the $\textit{adaptive}$ adversary could flip the label of an edge based on the current output of the algorithm. Our main result is a randomized algorithm that always maintains an $O(1)$-approximation to the optimal correlation clustering with $O(\log^{2}{n})$ amortized update time. Prior to our work, no algorithm with $O(1)$-approximation and $\text{polylog}{(n)}$ update time for the adversarially robust setting was known. We further validate our theoretical results with experiments on synthetic and real-world datasets with competitive empirical performances. Our main technical ingredient is an algorithm that maintains $\textit{sparse-dense decomposition}$ with $\text{polylog}{(n)}$ update time, which could be of independent interest.

Learning-augmented Maximum Independent Set

We study the Maximum Independent Set (MIS) problem on general graphs within the framework of learning-augmented algorithms. The MIS problem is known to be NP-hard and is also NP-hard to approximate to within a factor of $n^{1-\delta}$ for any $\delta>0$. We show that we can break this barrier in the presence of an oracle obtained through predictions from a machine learning model that answers vertex membership queries for a fixed MIS with probability $1/2+\varepsilon$. In the first setting we consider, the oracle can be queried once per vertex to know if a vertex belongs to a fixed MIS, and the oracle returns the correct answer with probability $1/2 + \varepsilon$. Under this setting, we show an algorithm that obtains an $\tilde{O}(\sqrt{\Delta}/\varepsilon)$-approximation in $O(m)$ time where $\Delta$ is the maximum degree of the graph. In the second setting, we allow multiple queries to the oracle for a vertex, each of which is correct with probability $1/2 + \varepsilon$. For this setting, we show an $O(1)$-approximation algorithm using $O(n/\varepsilon^2)$ total queries and $\tilde{O}(m)$ runtime.

Differentially Private Range Queries with Correlated Input Perturbation

This work proposes a class of locally differentially private mechanisms for linear queries, in particular range queries, that leverages correlated input perturbation to simultaneously achieve unbiasedness, consistency, statistical transparency, and control over utility requirements in terms of accuracy targets expressed either in certain query margins or as implied by the hierarchical database structure. The proposed Cascade Sampling algorithm instantiates the mechanism exactly and efficiently. Our bounds show that we obtain near-optimal utility while being empirically competitive against output perturbation methods.

An Energy-Based View of Graph Neural Networks

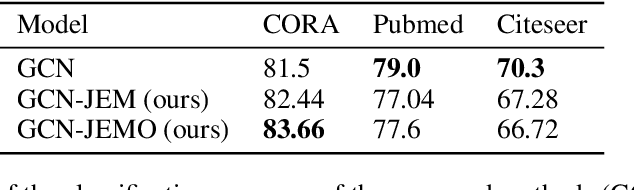
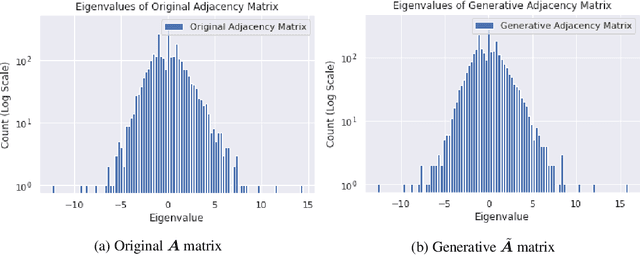
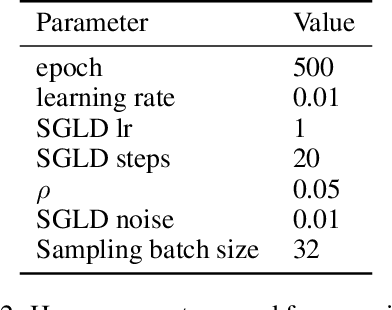
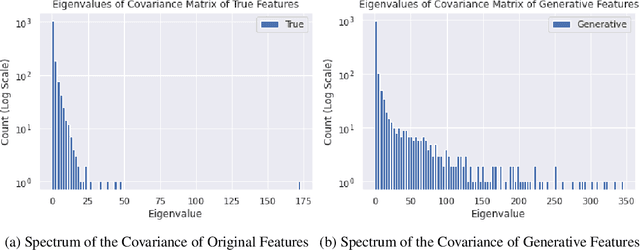
Graph neural networks are a popular variant of neural networks that work with graph-structured data. In this work, we consider combining graph neural networks with the energy-based view of Grathwohl et al. (2019) with the aim of obtaining a more robust classifier. We successfully implement this framework by proposing a novel method to ensure generation over features as well as the adjacency matrix and evaluate our method against the standard graph convolutional network (GCN) architecture (Kipf & Welling (2016)). Our approach obtains comparable discriminative performance while improving robustness, opening promising new directions for future research for energy-based graph neural networks.

Graph Learning for Inverse Landscape Genetics

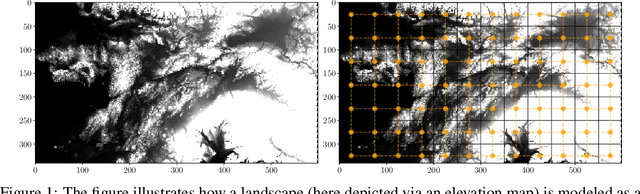
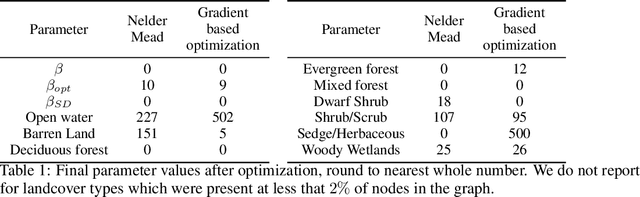
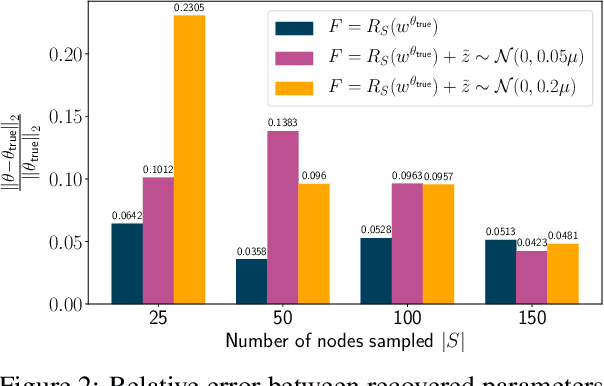
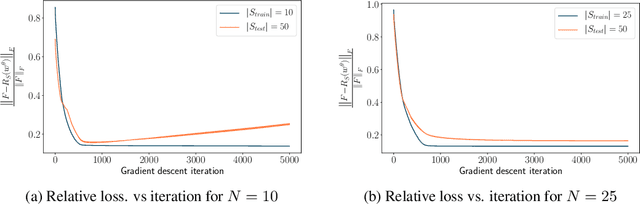
The problem of inferring unknown graph edges from numerical data at a graph's nodes appears in many forms across machine learning. We study a version of this problem that arises in the field of landscape genetics, where genetic similarity between populations of organisms living in a heterogeneous landscape is explained by a weighted graph that encodes the ease of dispersal through that landscape. Our main contribution is an efficient algorithm for inverse landscape genetics, which is the task of inferring this graph from measurements of genetic similarity at different locations (graph nodes). We reduced the problem to that of inferring graph edges from noisy measurements of effective resistances between graph nodes, which have been observed to correlate well with genetic similarity. Building on Hoskins et. al., we develop an efficient first-order optimization method for solving this problem. Despite its non-convex nature, extensive experiments on synthetic and real genetic data establish that our method provides fast and reliable convergence, significantly outperforming existing heuristics used in the field.