Amortized Rejection Sampling in Universal Probabilistic Programming

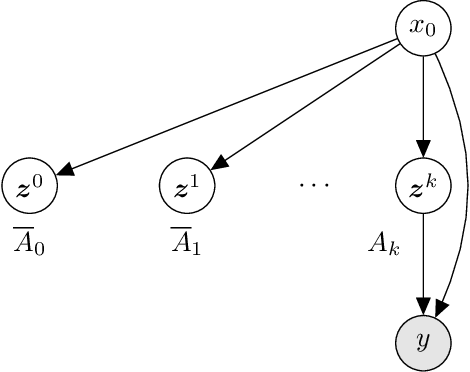
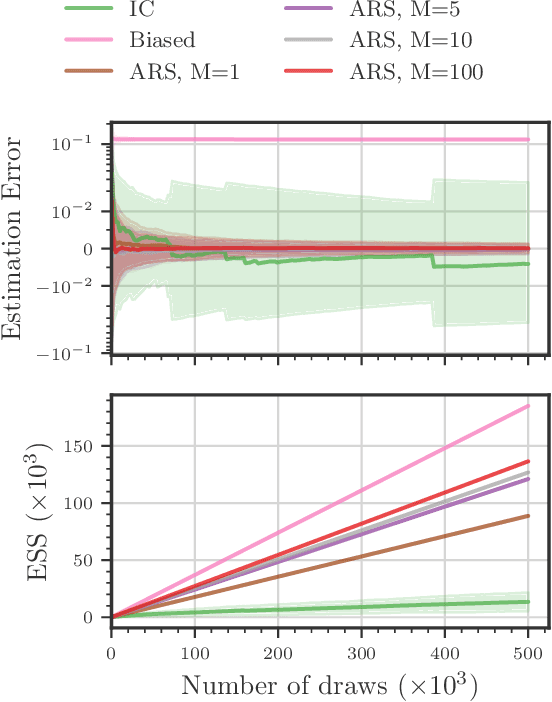
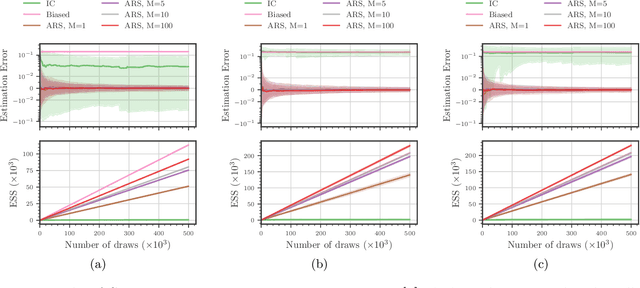
Existing approaches to amortized inference in probabilistic programs with unbounded loops can produce estimators with infinite variance. An instance of this is importance sampling inference in programs that explicitly include rejection sampling as part of the user-programmed generative procedure. In this paper we develop a new and efficient amortized importance sampling estimator. We prove finite variance of our estimator and empirically demonstrate our method's correctness and efficiency compared to existing alternatives on generative programs containing rejection sampling loops and discuss how to implement our method in a generic probabilistic programming framework.

A Unified Stochastic Gradient Approach to Designing Bayesian-Optimal Experiments

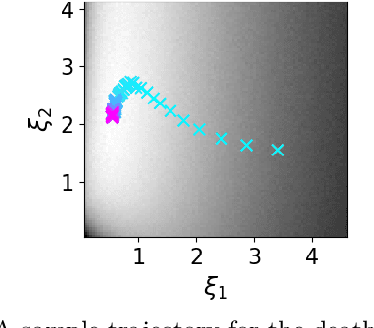
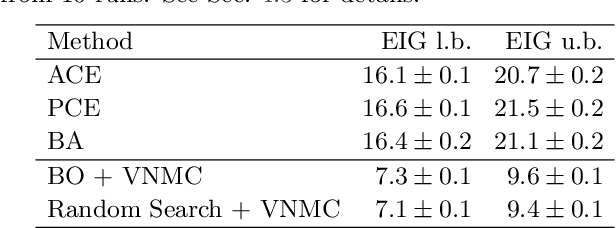
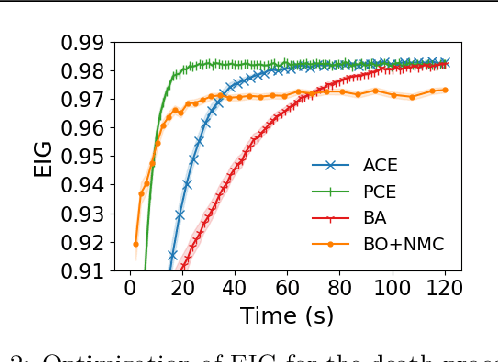
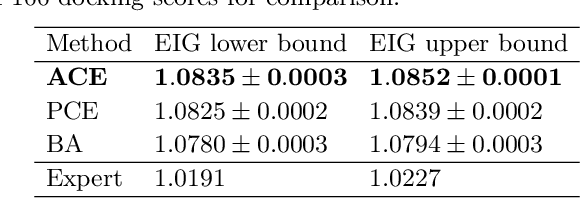
We introduce a fully stochastic gradient based approach to Bayesian optimal experimental design (BOED). This is achieved through the use of variational lower bounds on the expected information gain (EIG) of an experiment that can be simultaneously optimized with respect to both the variational and design parameters. This allows the design process to be carried out through a single unified stochastic gradient ascent procedure, in contrast to existing approaches that typically construct an EIG estimator on a pointwise basis, before passing this estimator to a separate optimizer. We show that this, in turn, leads to more efficient BOED schemes and provide a number of a different variational objectives suited to different settings. Furthermore, we show that our gradient-based approaches are able to provide effective design optimization in substantially higher dimensional settings than existing approaches.

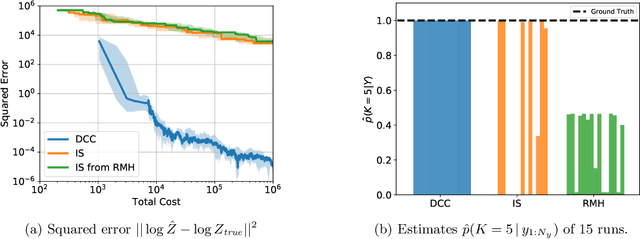
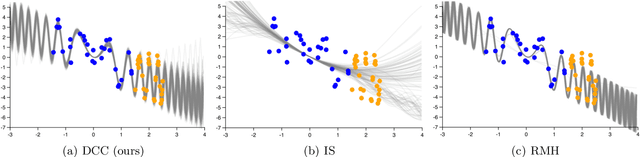
Divide, Conquer, and Combine: a New Inference Strategy for Probabilistic Programs with Stochastic Support

Universal probabilistic programming systems (PPSs) provide a powerful and expressive framework for specifying rich and complex probabilistic models. However, this expressiveness comes at the cost of substantially complicating the process of drawing inferences from the model. In particular, inference can become challenging when the support of the model varies between executions. Though general-purpose inference engines have been designed to operate in such settings, they are typically highly inefficient, often relying on proposing from the prior to make transitions. To address this, we introduce a new inference framework: Divide, Conquer, and Combine (DCC). DCC divides the program into separate straight-line sub-programs, each of which has a fixed support allowing more powerful inference algorithms to be run locally, before recombining their outputs in a principled fashion. We show how DCC can be implemented as an automated and general-purpose PPS inference engine, and empirically confirm that it can provide substantial performance improvements over previous approaches.

Amortized Monte Carlo Integration

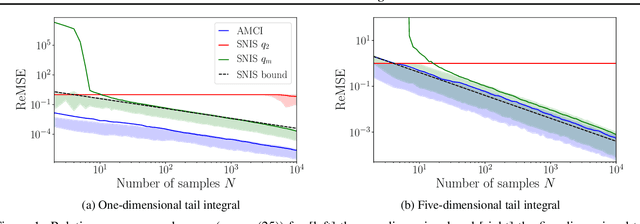
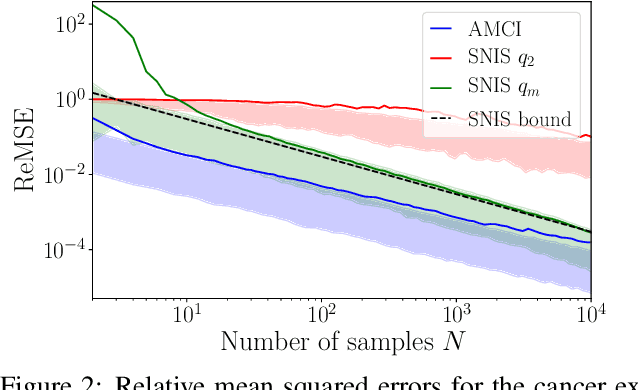
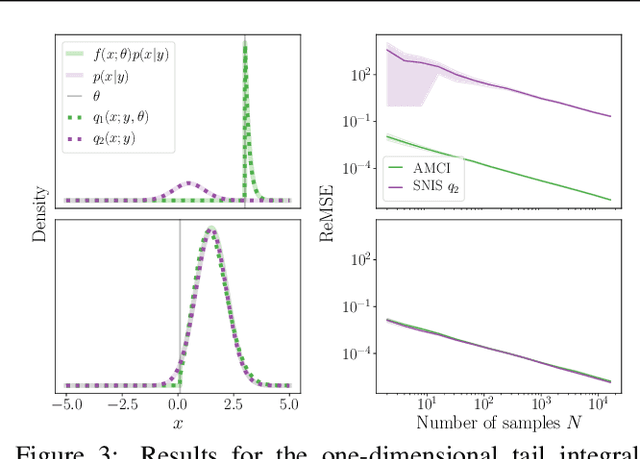
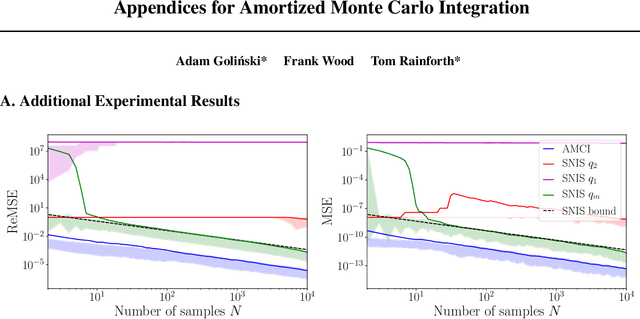
Current approaches to amortizing Bayesian inference focus solely on approximating the posterior distribution. Typically, this approximation is, in turn, used to calculate expectations for one or more target functions - a computational pipeline which is inefficient when the target function(s) are known upfront. In this paper, we address this inefficiency by introducing AMCI, a method for amortizing Monte Carlo integration directly. AMCI operates similarly to amortized inference but produces three distinct amortized proposals, each tailored to a different component of the overall expectation calculation. At runtime, samples are produced separately from each amortized proposal, before being combined to an overall estimate of the expectation. We show that while existing approaches are fundamentally limited in the level of accuracy they can achieve, AMCI can theoretically produce arbitrarily small errors for any integrable target function using only a single sample from each proposal at runtime. We further show that it is able to empirically outperform the theoretically optimal self-normalized importance sampler on a number of example problems. Furthermore, AMCI allows not only for amortizing over datasets but also amortizing over target functions.

On the Fairness of Disentangled Representations

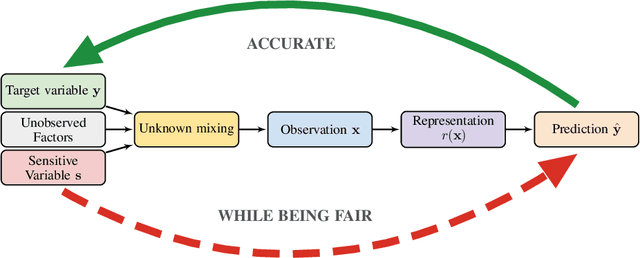
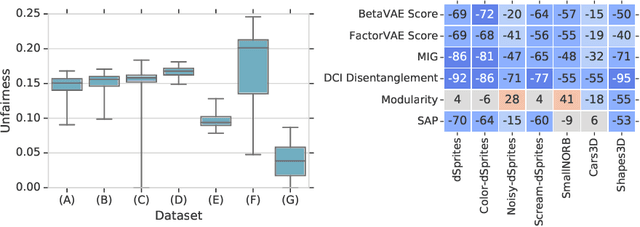
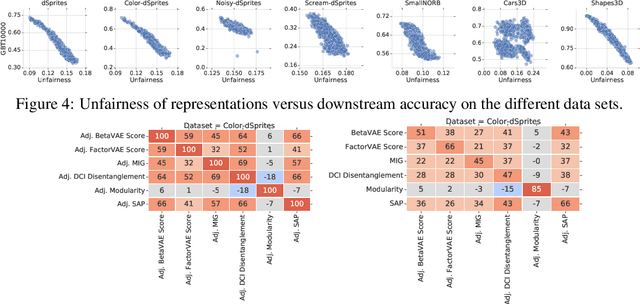
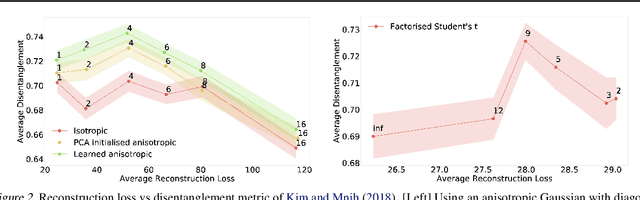
Recently there has been a significant interest in learning disentangled representations, as they promise increased interpretability, generalization to unseen scenarios and faster learning on downstream tasks. In this paper, we investigate the usefulness of different notions of disentanglement for improving the fairness of downstream prediction tasks based on representations. We consider the setting where the goal is to predict a target variable based on the learned representation of high-dimensional observations (such as images) that depend on both the target variable and an unobserved sensitive variable. We show that in this setting both the optimal and empirical predictions can be unfair, even if the target variable and the sensitive variable are independent. Analyzing more than 12600 trained representations of state-of-the-art disentangled models, we observe that various disentanglement scores are consistently correlated with increased fairness, suggesting that disentanglement may be a useful property to encourage fairness when sensitive variables are not observed.

Hijacking Malaria Simulators with Probabilistic Programming

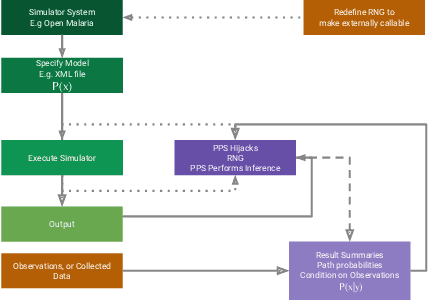
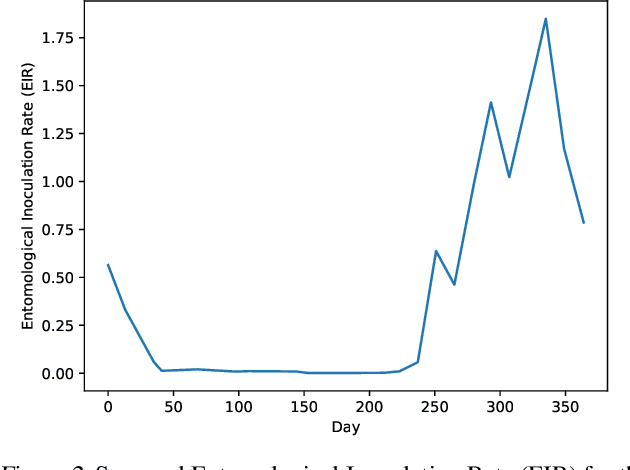
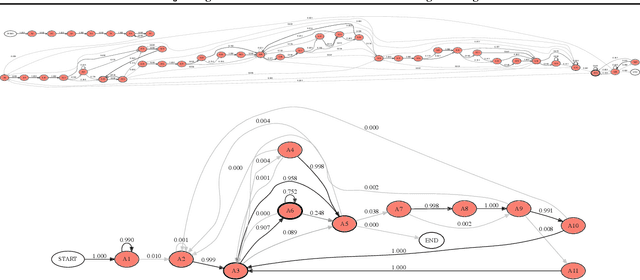
Epidemiology simulations have become a fundamental tool in the fight against the epidemics of various infectious diseases like AIDS and malaria. However, the complicated and stochastic nature of these simulators can mean their output is difficult to interpret, which reduces their usefulness to policymakers. In this paper, we introduce an approach that allows one to treat a large class of population-based epidemiology simulators as probabilistic generative models. This is achieved by hijacking the internal random number generator calls, through the use of a universal probabilistic programming system (PPS). In contrast to other methods, our approach can be easily retrofitted to simulators written in popular industrial programming frameworks. We demonstrate that our method can be used for interpretable introspection and inference, thus shedding light on black-box simulators. This reinstates much-needed trust between policymakers and evidence-based methods.

Variational Estimators for Bayesian Optimal Experimental Design

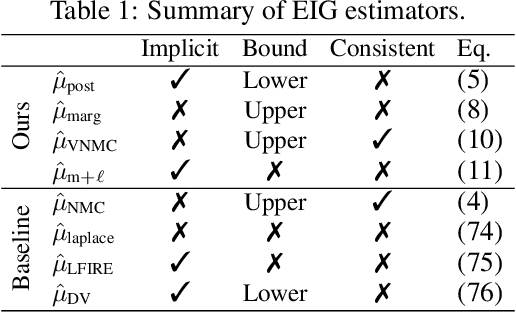
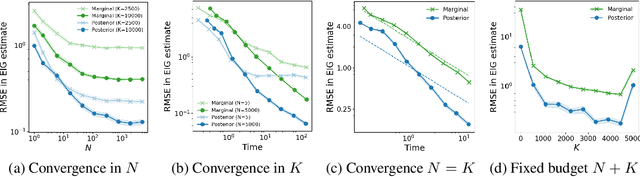
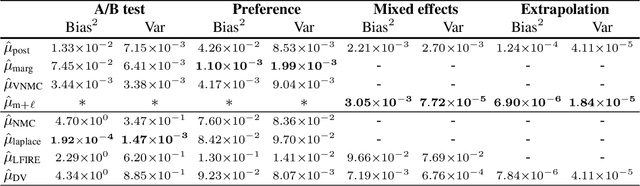
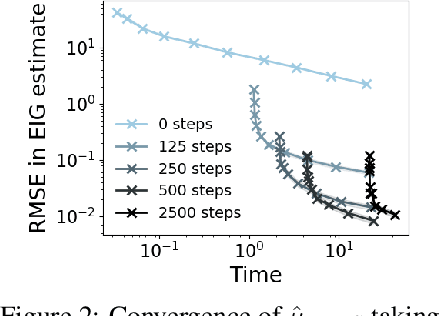
Bayesian optimal experimental design (BOED) is a principled framework for making efficient use of limited experimental resources. Unfortunately, its applicability is hampered by the difficulty of obtaining accurate estimates of the expected information gain (EIG) of an experiment. To address this, we introduce several classes of fast EIG estimators suited to the experiment design context by building on ideas from variational inference and mutual information estimation. We show theoretically and empirically that these estimators can provide significant gains in speed and accuracy over previous approaches. We demonstrate the practicality of our approach via a number of experiments, including an adaptive experiment with human participants.

LF-PPL: A Low-Level First Order Probabilistic Programming Language for Non-Differentiable Models

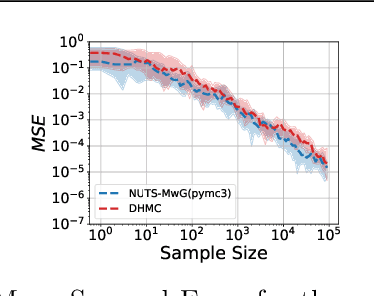
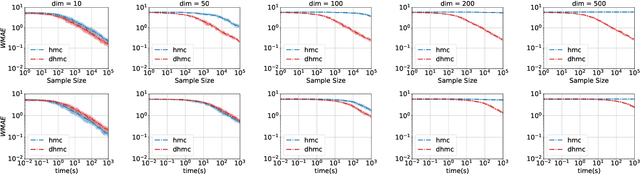
We develop a new Low-level, First-order Probabilistic Programming Language (LF-PPL) suited for models containing a mix of continuous, discrete, and/or piecewise-continuous variables. The key success of this language and its compilation scheme is in its ability to automatically distinguish parameters the density function is discontinuous with respect to, while further providing runtime checks for boundary crossings. This enables the introduction of new inference engines that are able to exploit gradient information, while remaining efficient for models which are not everywhere differentiable. We demonstrate this ability by incorporating a discontinuous Hamiltonian Monte Carlo (DHMC) inference engine that is able to deliver automated and efficient inference for non-differentiable models. Our system is backed up by a mathematical formalism that ensures that any model expressed in this language has a density with measure zero discontinuities to maintain the validity of the inference engine.

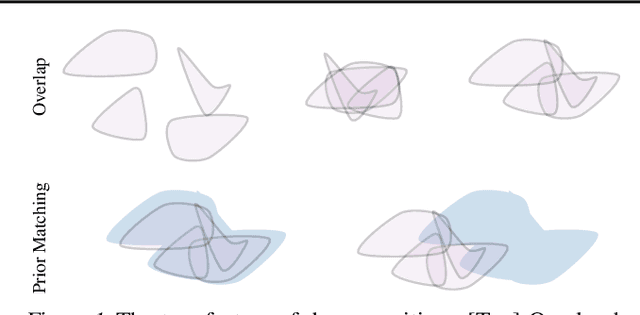
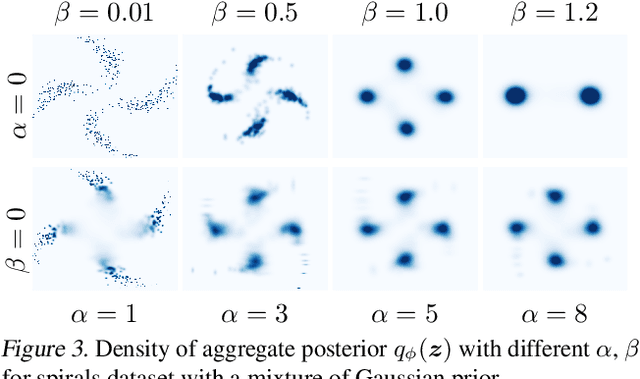
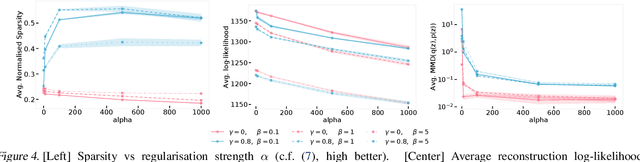
Disentangling Disentanglement

We develop a generalised notion of disentanglement in Variational Auto-Encoders (VAEs) by casting it as a \emph{decomposition} of the latent representation, characterised by i) enforcing an appropriate level of overlap in the latent encodings of the data, and ii) regularisation of the average encoding to a desired structure, represented through the prior. We motivate this by showing that a) the $\beta$-VAE disentangles purely through regularisation of the overlap in latent encodings, and through its average (Gaussian) encoder variance, and b) disentanglement, as independence between latents, can be cast as a regularisation of the aggregate posterior to a prior with specific characteristics. We validate this characterisation by showing that simple manipulations of these factors, such as using rotationally variant priors, can help improve disentanglement, and discuss how this characterisation provides a more general framework to incorporate notions of decomposition beyond just independence between the latents.

A Statistical Approach to Assessing Neural Network Robustness

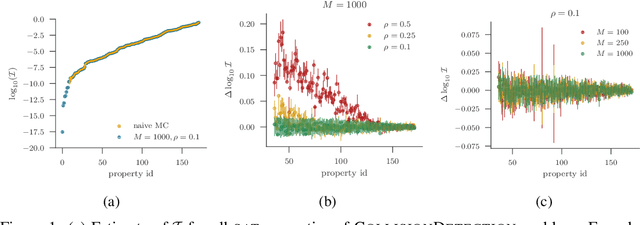
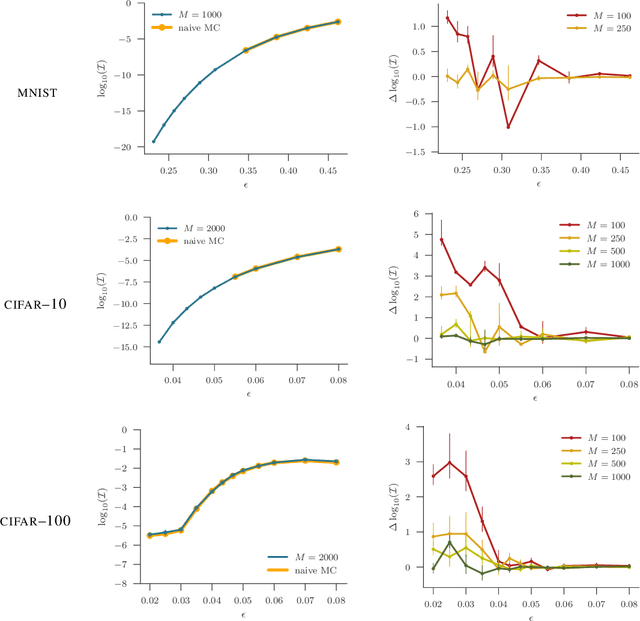
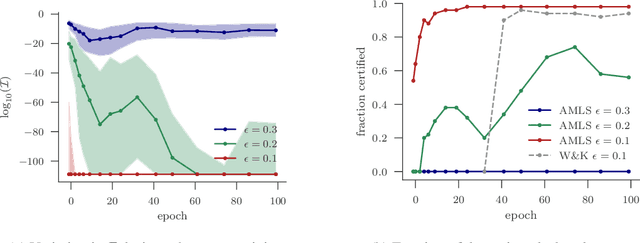
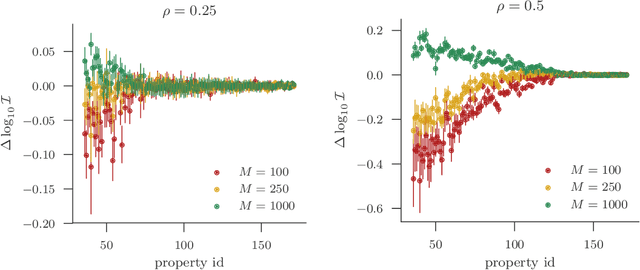
We present a new approach to assessing the robustness of neural networks based on estimating the proportion of inputs for which a property is violated. Specifically, we estimate the probability of the event that the property is violated under an input model. Our approach critically varies from the formal verification framework in that when the property can be violated, it provides an informative notion of how robust the network is, rather than just the conventional assertion that the network is not verifiable. Furthermore, it provides an ability to scale to larger networks than formal verification approaches. Though the framework still provides a formal guarantee of satisfiability whenever it successfully finds one or more violations, these advantages do come at the cost of only providing a statistical estimate of unsatisfiability whenever no violation is found. Key to the practical success of our approach is an adaptation of multi-level splitting, a Monte Carlo approach for estimating the probability of rare events, to our statistical robustness framework. We demonstrate that our approach is able to emulate formal verification procedures on benchmark problems, while scaling to larger networks and providing reliable additional information in the form of accurate estimates of the violation probability.