Variational Partial Group Convolutions for Input-Aware Partial Equivariance of Rotations and Color-Shifts

Group Equivariant CNNs (G-CNNs) have shown promising efficacy in various tasks, owing to their ability to capture hierarchical features in an equivariant manner. However, their equivariance is fixed to the symmetry of the whole group, limiting adaptability to diverse partial symmetries in real-world datasets, such as limited rotation symmetry of handwritten digit images and limited color-shift symmetry of flower images. Recent efforts address this limitation, one example being Partial G-CNN which restricts the output group space of convolution layers to break full equivariance. However, such an approach still fails to adjust equivariance levels across data. In this paper, we propose a novel approach, Variational Partial G-CNN (VP G-CNN), to capture varying levels of partial equivariance specific to each data instance. VP G-CNN redesigns the distribution of the output group elements to be conditioned on input data, leveraging variational inference to avoid overfitting. This enables the model to adjust its equivariance levels according to the needs of individual data points. Additionally, we address training instability inherent in discrete group equivariance models by redesigning the reparametrizable distribution. We demonstrate the effectiveness of VP G-CNN on both toy and real-world datasets, including MNIST67-180, CIFAR10, ColorMNIST, and Flowers102. Our results show robust performance, even in uncertainty metrics.

An Infinite-Width Analysis on the Jacobian-Regularised Training of a Neural Network

The recent theoretical analysis of deep neural networks in their infinite-width limits has deepened our understanding of initialisation, feature learning, and training of those networks, and brought new practical techniques for finding appropriate hyperparameters, learning network weights, and performing inference. In this paper, we broaden this line of research by showing that this infinite-width analysis can be extended to the Jacobian of a deep neural network. We show that a multilayer perceptron (MLP) and its Jacobian at initialisation jointly converge to a Gaussian process (GP) as the widths of the MLP's hidden layers go to infinity and characterise this GP. We also prove that in the infinite-width limit, the evolution of the MLP under the so-called robust training (i.e., training with a regulariser on the Jacobian) is described by a linear first-order ordinary differential equation that is determined by a variant of the Neural Tangent Kernel. We experimentally show the relevance of our theoretical claims to wide finite networks, and empirically analyse the properties of kernel regression solution to obtain an insight into Jacobian regularisation.

Learning Symmetrization for Equivariance with Orbit Distance Minimization

We present a general framework for symmetrizing an arbitrary neural-network architecture and making it equivariant with respect to a given group. We build upon the proposals of Kim et al. (2023); Kaba et al. (2023) for symmetrization, and improve them by replacing their conversion of neural features into group representations, with an optimization whose loss intuitively measures the distance between group orbits. This change makes our approach applicable to a broader range of matrix groups, such as the Lorentz group O(1, 3), than these two proposals. We experimentally show our method's competitiveness on the SO(2) image classification task, and also its increased generality on the task with O(1, 3). Our implementation will be made accessible at https://github.com/tiendatnguyen-vision/Orbit-symmetrize.

Regularizing Towards Soft Equivariance Under Mixed Symmetries

Datasets often have their intrinsic symmetries, and particular deep-learning models called equivariant or invariant models have been developed to exploit these symmetries. However, if some or all of these symmetries are only approximate, which frequently happens in practice, these models may be suboptimal due to the architectural restrictions imposed on them. We tackle this issue of approximate symmetries in a setup where symmetries are mixed, i.e., they are symmetries of not single but multiple different types and the degree of approximation varies across these types. Instead of proposing a new architectural restriction as in most of the previous approaches, we present a regularizer-based method for building a model for a dataset with mixed approximate symmetries. The key component of our method is what we call equivariance regularizer for a given type of symmetries, which measures how much a model is equivariant with respect to the symmetries of the type. Our method is trained with these regularizers, one per each symmetry type, and the strength of the regularizers is automatically tuned during training, leading to the discovery of the approximation levels of some candidate symmetry types without explicit supervision. Using synthetic function approximation and motion forecasting tasks, we demonstrate that our method achieves better accuracy than prior approaches while discovering the approximate symmetry levels correctly.

Over-parameterised Shallow Neural Networks with Asymmetrical Node Scaling: Global Convergence Guarantees and Feature Learning

We consider the optimisation of large and shallow neural networks via gradient flow, where the output of each hidden node is scaled by some positive parameter. We focus on the case where the node scalings are non-identical, differing from the classical Neural Tangent Kernel (NTK) parameterisation. We prove that, for large neural networks, with high probability, gradient flow converges to a global minimum AND can learn features, unlike in the NTK regime. We also provide experiments on synthetic and real-world datasets illustrating our theoretical results and showing the benefit of such scaling in terms of pruning and transfer learning.

Smoothness Analysis for Probabilistic Programs with Application to Optimised Variational Inference

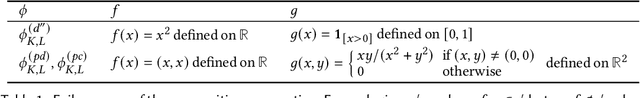
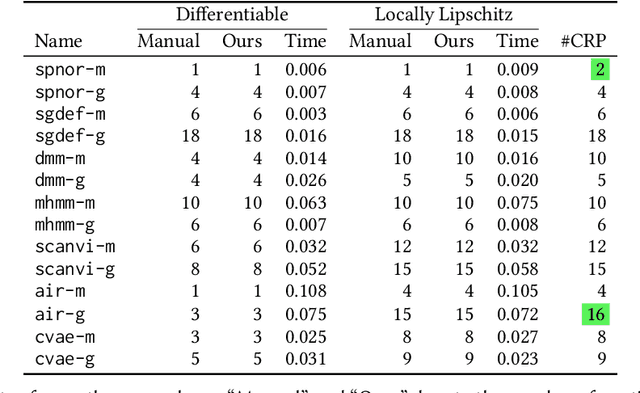
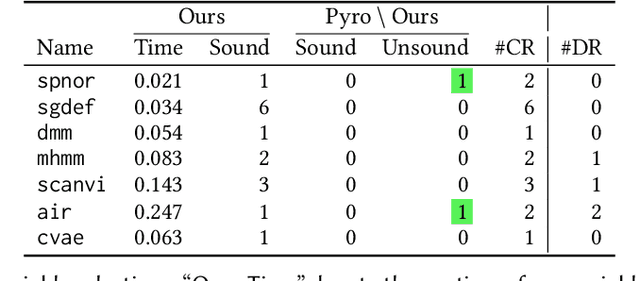
We present a static analysis for discovering differentiable or more generally smooth parts of a given probabilistic program, and show how the analysis can be used to improve the pathwise gradient estimator, one of the most popular methods for posterior inference and model learning. Our improvement increases the scope of the estimator from differentiable models to non-differentiable ones without requiring manual intervention of the user; the improved estimator automatically identifies differentiable parts of a given probabilistic program using our static analysis, and applies the pathwise gradient estimator to the identified parts while using a more general but less efficient estimator, called score estimator, for the rest of the program. Our analysis has a surprisingly subtle soundness argument, partly due to the misbehaviours of some target smoothness properties when viewed from the perspective of program analysis designers. For instance, some smoothness properties are not preserved by function composition, and this makes it difficult to analyse sequential composition soundly without heavily sacrificing precision. We formulate five assumptions on a target smoothness property, prove the soundness of our analysis under those assumptions, and show that our leading examples satisfy these assumptions. We also show that by using information from our analysis, our improved gradient estimator satisfies an important differentiability requirement and thus, under a mild regularity condition, computes the correct estimate on average, i.e., it returns an unbiased estimate. Our experiments with representative probabilistic programs in the Pyro language show that our static analysis is capable of identifying smooth parts of those programs accurately, and making our improved pathwise gradient estimator exploit all the opportunities for high performance in those programs.

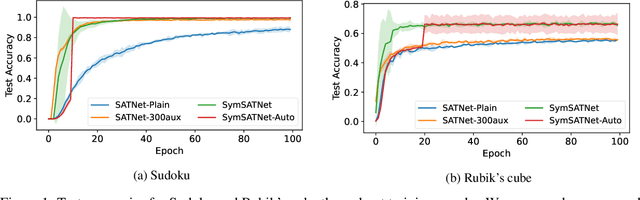
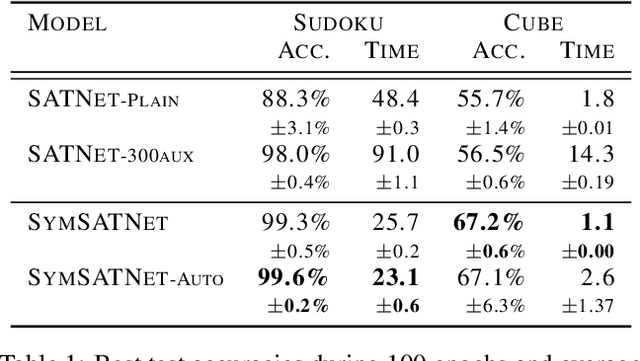
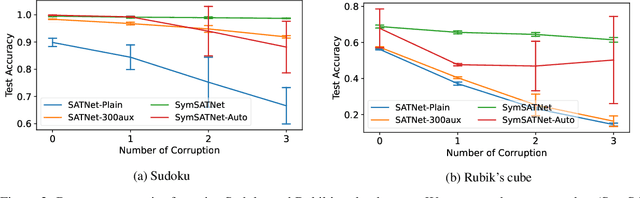
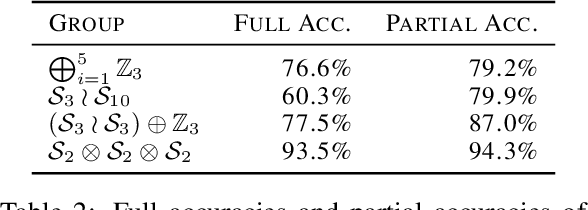
Learning Symmetric Rules with SATNet

SATNet is a differentiable constraint solver with a custom backpropagation algorithm, which can be used as a layer in a deep-learning system. It is a promising proposal for bridging deep learning and logical reasoning. In fact, SATNet has been successfully applied to learn, among others, the rules of a complex logical puzzle, such as Sudoku, just from input and output pairs where inputs are given as images. In this paper, we show how to improve the learning of SATNet by exploiting symmetries in the target rules of a given but unknown logical puzzle or more generally a logical formula. We present SymSATNet, a variant of SATNet that translates the given symmetries of the target rules to a condition on the parameters of SATNet and requires that the parameters should have a particular parametric form that guarantees the condition. The requirement dramatically reduces the number of parameters to learn for the rules with enough symmetries, and makes the parameter learning of SymSATNet much easier than that of SATNet. We also describe a technique for automatically discovering symmetries of the target rules from examples. Our experiments with Sudoku and Rubik's cube show the substantial improvement of SymSATNet over the baseline SATNet.

Deep neural networks with dependent weights: Gaussian Process mixture limit, heavy tails, sparsity and compressibility

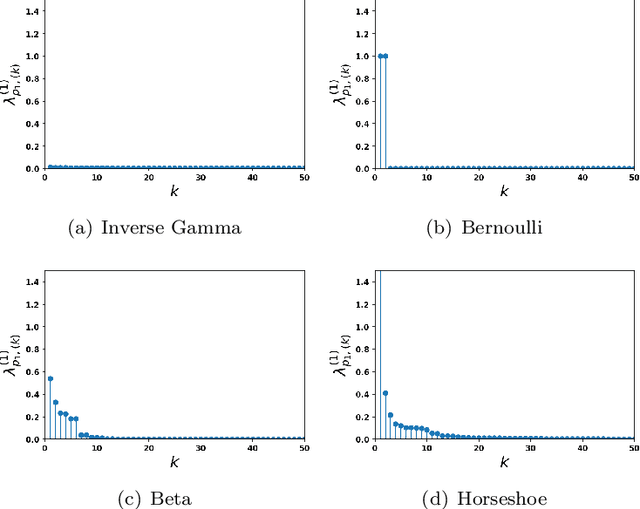
This article studies the infinite-width limit of deep feedforward neural networks whose weights are dependent, and modelled via a mixture of Gaussian distributions. Each hidden node of the network is assigned a nonnegative random variable that controls the variance of the outgoing weights of that node. We make minimal assumptions on these per-node random variables: they are iid and their sum, in each layer, converges to some finite random variable in the infinite-width limit. Under this model, we show that each layer of the infinite-width neural network can be characterised by two simple quantities: a non-negative scalar parameter and a L\'evy measure on the positive reals. If the scalar parameters are strictly positive and the L\'evy measures are trivial at all hidden layers, then one recovers the classical Gaussian process (GP) limit, obtained with iid Gaussian weights. More interestingly, if the L\'evy measure of at least one layer is non-trivial, we obtain a mixture of Gaussian processes (MoGP) in the large-width limit. The behaviour of the neural network in this regime is very different from the GP regime. One obtains correlated outputs, with non-Gaussian distributions, possibly with heavy tails. Additionally, we show that, in this regime, the weights are compressible, and feature learning is possible. Many sparsity-promoting neural network models can be recast as special cases of our approach, and we discuss their infinite-width limits; we also present an asymptotic analysis of the pruning error. We illustrate some of the benefits of the MoGP regime over the GP regime in terms of representation learning and compressibility on simulated, MNIST and Fashion MNIST datasets.

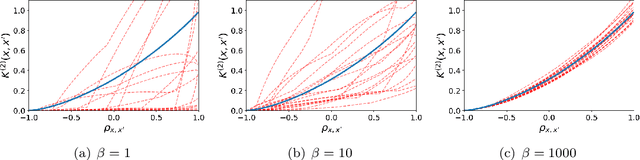
LobsDICE: Offline Imitation Learning from Observation via Stationary Distribution Correction Estimation

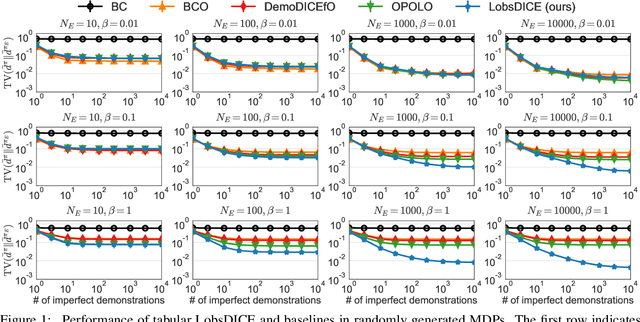
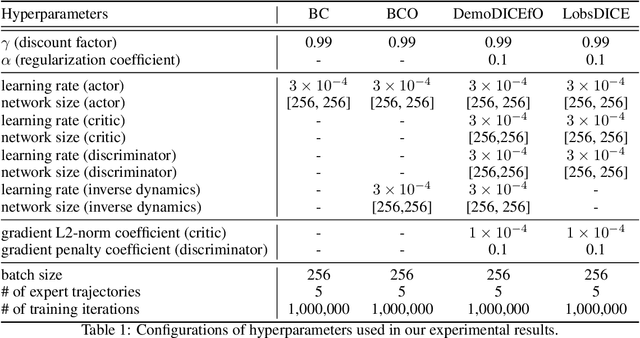
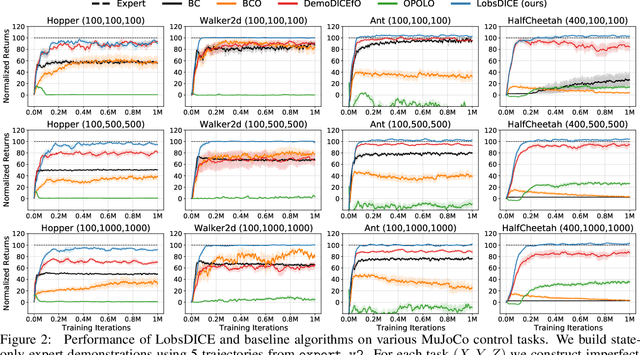
We consider the problem of imitation from observation (IfO), in which the agent aims to mimic the expert's behavior from the state-only demonstrations by experts. We additionally assume that the agent cannot interact with the environment but has access to the action-labeled transition data collected by some agent with unknown quality. This offline setting for IfO is appealing in many real-world scenarios where the ground-truth expert actions are inaccessible and the arbitrary environment interactions are costly or risky. In this paper, we present LobsDICE, an offline IfO algorithm that learns to imitate the expert policy via optimization in the space of stationary distributions. Our algorithm solves a single convex minimization problem, which minimizes the divergence between the two state-transition distributions induced by the expert and the agent policy. On an extensive set of offline IfO tasks, LobsDICE shows promising results, outperforming strong baseline algorithms.

Scale Mixtures of Neural Network Gaussian Processes

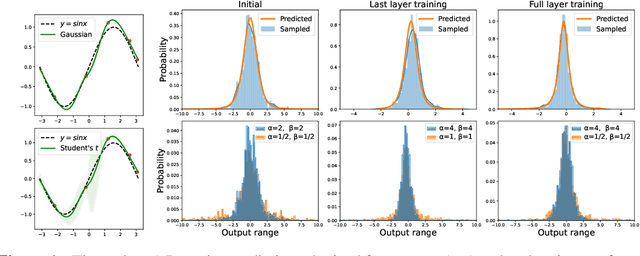
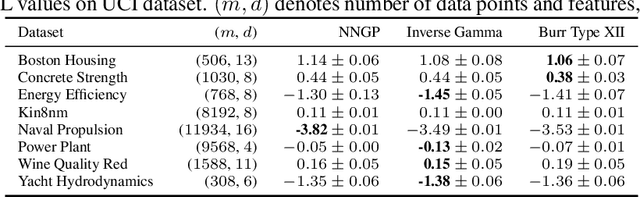
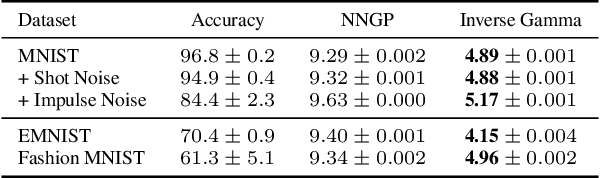
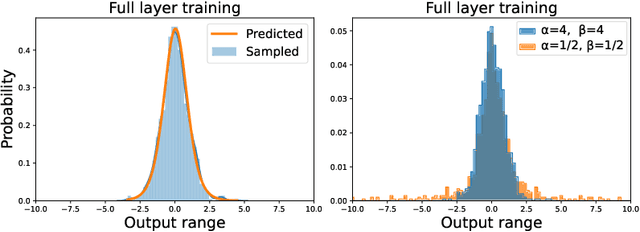
Recent works have revealed that infinitely-wide feed-forward or recurrent neural networks of any architecture correspond to Gaussian processes referred to as $\mathrm{NNGP}$. While these works have extended the class of neural networks converging to Gaussian processes significantly, however, there has been little focus on broadening the class of stochastic processes that such neural networks converge to. In this work, inspired by the scale mixture of Gaussian random variables, we propose the scale mixture of $\mathrm{NNGP}$ for which we introduce a prior distribution on the scale of the last-layer parameters. We show that simply introducing a scale prior on the last-layer parameters can turn infinitely-wide neural networks of any architecture into a richer class of stochastic processes. Especially, with certain scale priors, we obtain heavy-tailed stochastic processes, and we recover Student's $t$ processes in the case of inverse gamma priors. We further analyze the distributions of the neural networks initialized with our prior setting and trained with gradient descents and obtain similar results as for $\mathrm{NNGP}$. We present a practical posterior-inference algorithm for the scale mixture of $\mathrm{NNGP}$ and empirically demonstrate its usefulness on regression and classification tasks.