On Statistical Bias In Active Learning: How and When To Fix It

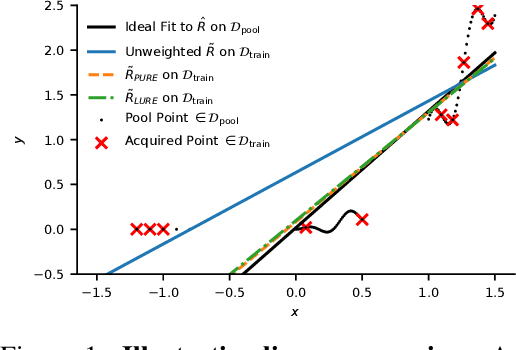
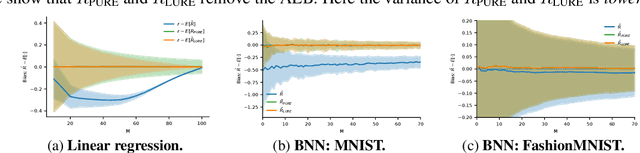
Active learning is a powerful tool when labelling data is expensive, but it introduces a bias because the training data no longer follows the population distribution. We formalize this bias and investigate the situations in which it can be harmful and sometimes even helpful. We further introduce novel corrective weights to remove bias when doing so is beneficial. Through this, our work not only provides a useful mechanism that can improve the active learning approach, but also an explanation of the empirical successes of various existing approaches which ignore this bias. In particular, we show that this bias can be actively helpful when training overparameterized models -- like neural networks -- with relatively little data.

On Signal-to-Noise Ratio Issues in Variational Inference for Deep Gaussian Processes

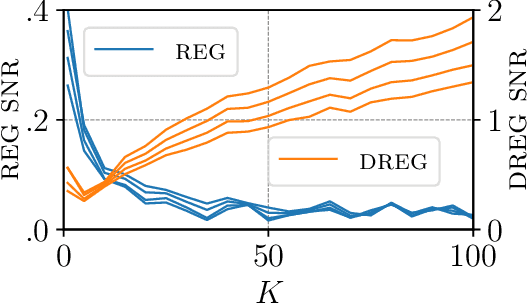
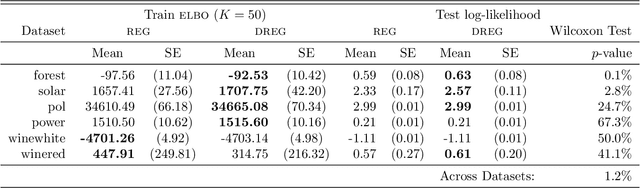
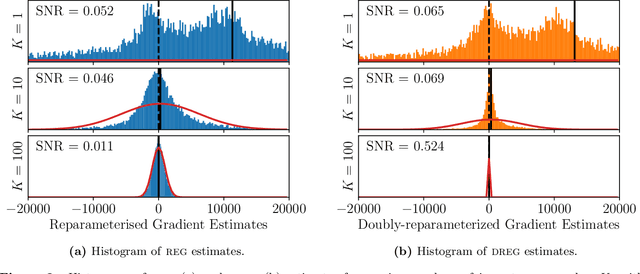
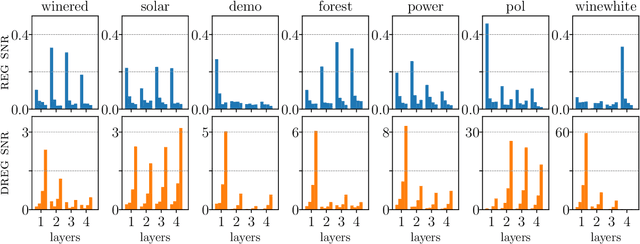
We show that the gradient estimates used in training Deep Gaussian Processes (DGPs) with importance-weighted variational inference are susceptible to signal-to-noise ratio (SNR) issues. Specifically, we show both theoretically and empirically that the SNR of the gradient estimates for the latent variable's variational parameters decreases as the number of importance samples increases. As a result, these gradient estimates degrade to pure noise if the number of importance samples is too large. To address this pathology, we show how doubly-reparameterized gradient estimators, originally proposed for training variational autoencoders, can be adapted to the DGP setting and that the resultant estimators completely remedy the SNR issue, thereby providing more reliable training. Finally, we demonstrate that our fix can lead to improvements in the predictive performance of the model's predictive posterior.

Improving Transformation Invariance in Contrastive Representation Learning

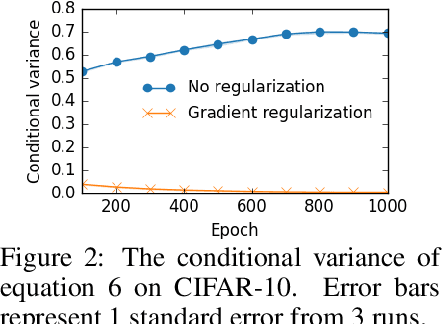
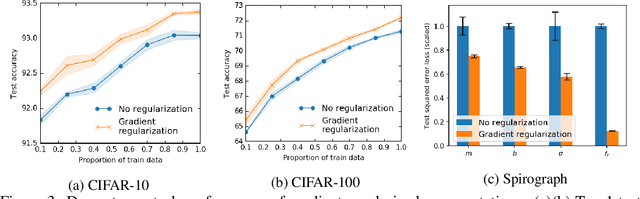
We propose methods to strengthen the invariance properties of representations obtained by contrastive learning. While existing approaches implicitly induce a degree of invariance as representations are learned, we look to more directly enforce invariance in the encoding process. To this end, we first introduce a training objective for contrastive learning that uses a novel regularizer to control how the representation changes under transformation. We show that representations trained with this objective perform better on downstream tasks and are more robust to the introduction of nuisance transformations at test time. Second, we propose a change to how test time representations are generated by introducing a feature averaging approach that combines encodings from multiple transformations of the original input, finding that this leads to across the board performance gains. Finally, we introduce the novel Spirograph dataset to explore our ideas in the context of a differentiable generative process with multiple downstream tasks, showing that our techniques for learning invariance are highly beneficial.

Towards a Theoretical Understanding of the Robustness of Variational Autoencoders

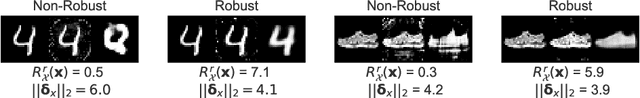
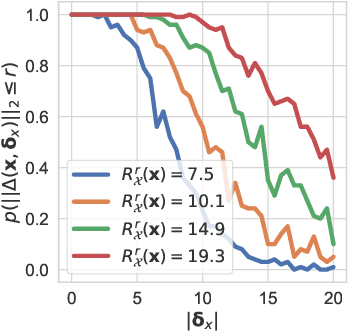
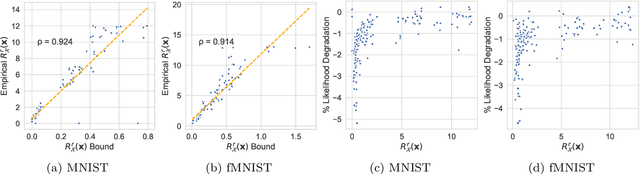
We make inroads into understanding the robustness of Variational Autoencoders (VAEs) to adversarial attacks and other input perturbations. While previous work has developed algorithmic approaches to attacking and defending VAEs, there remains a lack of formalization for what it means for a VAE to be robust. To address this, we develop a novel criterion for robustness in probabilistic models: $r$-robustness. We then use this to construct the first theoretical results for the robustness of VAEs, deriving margins in the input space for which we can provide guarantees about the resulting reconstruction. Informally, we are able to define a region within which any perturbation will produce a reconstruction that is similar to the original reconstruction. To support our analysis, we show that VAEs trained using disentangling methods not only score well under our robustness metrics, but that the reasons for this can be interpreted through our theoretical results.

Rethinking Semi-Supervised Learning in VAEs

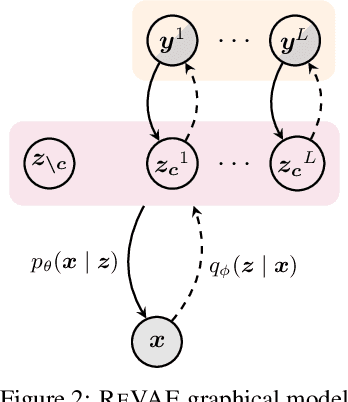
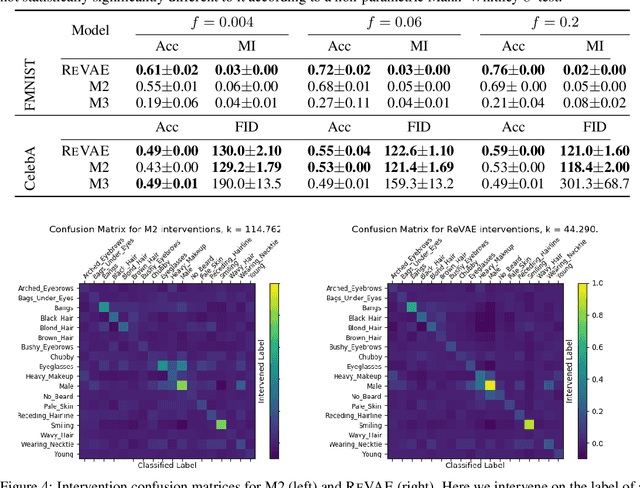
We present an alternative approach to semi-supervision in variational autoencoders(VAEs) that incorporates labels through auxiliary variables rather than directly through the latent variables. Prior work has generally conflated the meaning of labels, i.e. the associated characteristics of interest, with the actual label values themselves-learning latent variables that directly correspond to the label values. We argue that to learn meaningful representations, semi-supervision should instead try to capture these richer characteristics and that the construction of latent variables as label values is not just unnecessary, but actively harmful. To this end, we develop a novel VAE model, the reparameterized VAE (ReVAE), which "reparameterizes" supervision through auxiliary variables and a concomitant variational objective. Through judicious structuring of mappings between latent and auxiliary variables, we show that the ReVAE can effectively learn meaningful representations of data. In particular, we demonstrate that the ReVAE is able to match, and even improve on the classification accuracy of previous approaches, but more importantly, it also allows for more effective and more general interventions to be performed. We include a demo of ReVAE at https://github.com/thwjoy/revae-demo.

Statistically Robust Neural Network Classification

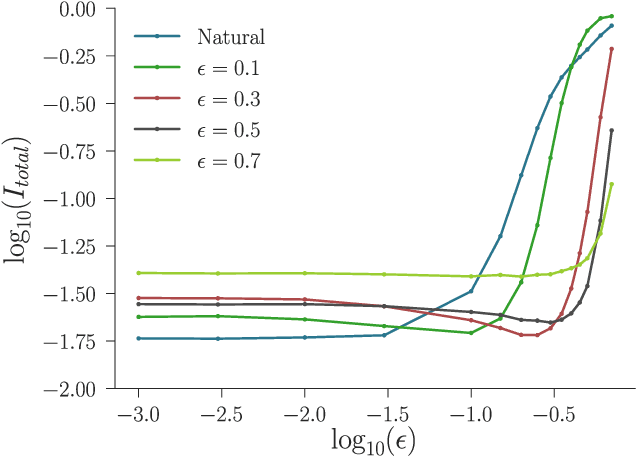
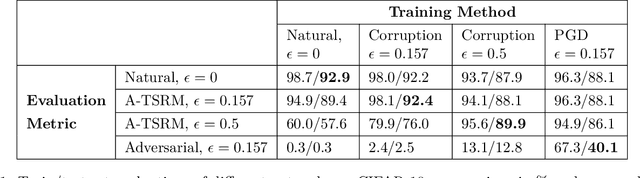
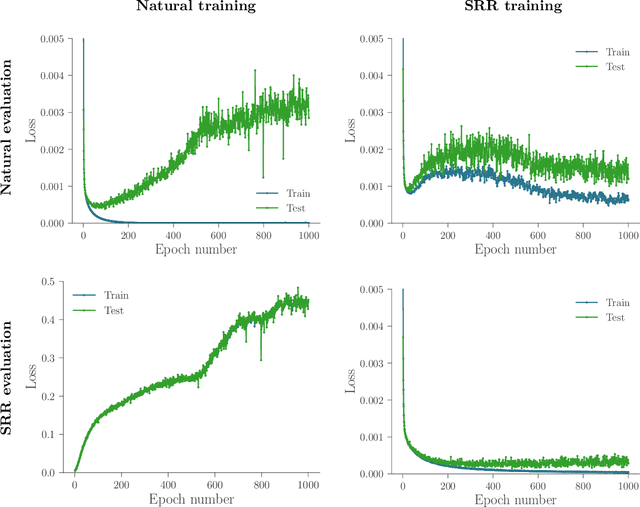
Recently there has been much interest in quantifying the robustness of neural network classifiers through adversarial risk metrics. However, for problems where test-time corruptions occur in a probabilistic manner, rather than being generated by an explicit adversary, adversarial metrics typically do not provide an accurate or reliable indicator of robustness. To address this, we introduce a statistically robust risk (SRR) framework which measures robustness in expectation over both network inputs and a corruption distribution. Unlike many adversarial risk metrics, which typically require separate applications on a point-by-point basis, the SRR can easily be directly estimated for an entire network and used as a training objective in a stochastic gradient scheme. Furthermore, we show both theoretically and empirically that it can scale to higher-dimensional networks by providing superior generalization performance compared with comparable adversarial risks.

Amortized Rejection Sampling in Universal Probabilistic Programming

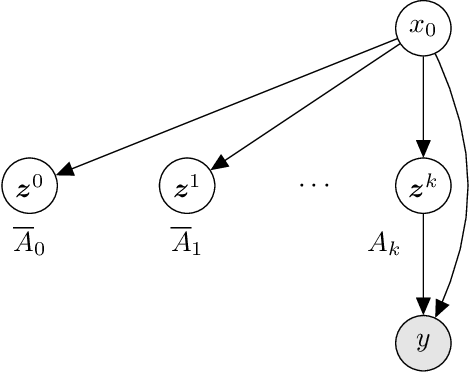
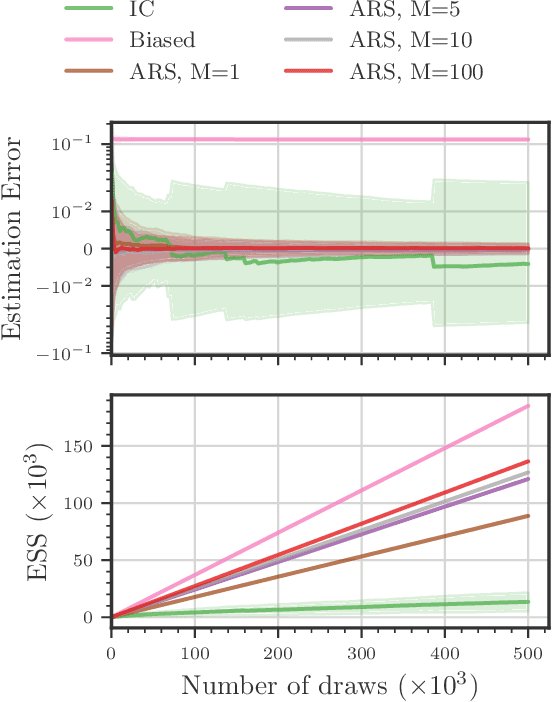
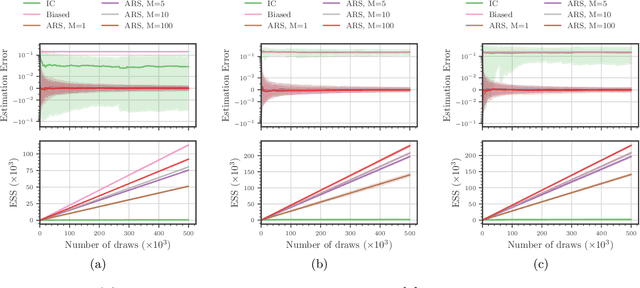
Existing approaches to amortized inference in probabilistic programs with unbounded loops can produce estimators with infinite variance. An instance of this is importance sampling inference in programs that explicitly include rejection sampling as part of the user-programmed generative procedure. In this paper we develop a new and efficient amortized importance sampling estimator. We prove finite variance of our estimator and empirically demonstrate our method's correctness and efficiency compared to existing alternatives on generative programs containing rejection sampling loops and discuss how to implement our method in a generic probabilistic programming framework.

A Unified Stochastic Gradient Approach to Designing Bayesian-Optimal Experiments

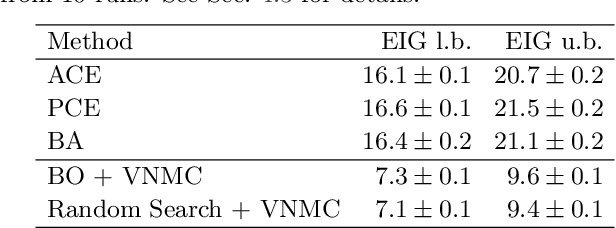
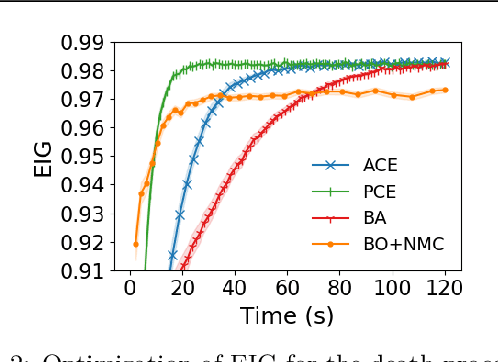
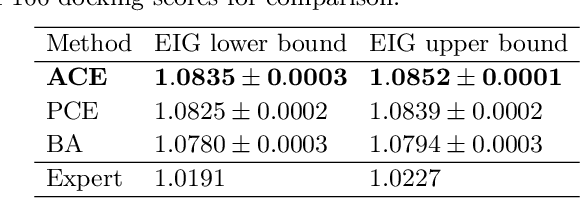
We introduce a fully stochastic gradient based approach to Bayesian optimal experimental design (BOED). This is achieved through the use of variational lower bounds on the expected information gain (EIG) of an experiment that can be simultaneously optimized with respect to both the variational and design parameters. This allows the design process to be carried out through a single unified stochastic gradient ascent procedure, in contrast to existing approaches that typically construct an EIG estimator on a pointwise basis, before passing this estimator to a separate optimizer. We show that this, in turn, leads to more efficient BOED schemes and provide a number of a different variational objectives suited to different settings. Furthermore, we show that our gradient-based approaches are able to provide effective design optimization in substantially higher dimensional settings than existing approaches.

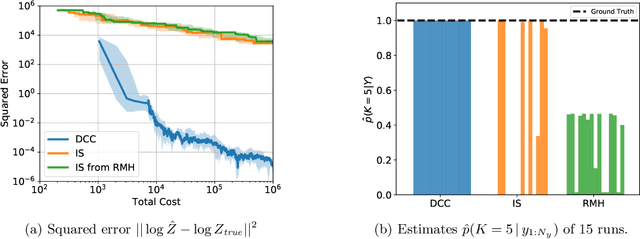
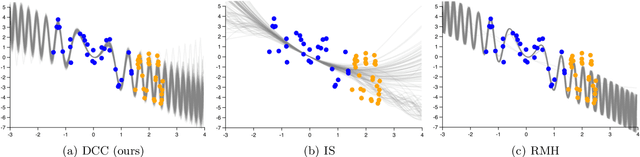
Divide, Conquer, and Combine: a New Inference Strategy for Probabilistic Programs with Stochastic Support

Universal probabilistic programming systems (PPSs) provide a powerful and expressive framework for specifying rich and complex probabilistic models. However, this expressiveness comes at the cost of substantially complicating the process of drawing inferences from the model. In particular, inference can become challenging when the support of the model varies between executions. Though general-purpose inference engines have been designed to operate in such settings, they are typically highly inefficient, often relying on proposing from the prior to make transitions. To address this, we introduce a new inference framework: Divide, Conquer, and Combine (DCC). DCC divides the program into separate straight-line sub-programs, each of which has a fixed support allowing more powerful inference algorithms to be run locally, before recombining their outputs in a principled fashion. We show how DCC can be implemented as an automated and general-purpose PPS inference engine, and empirically confirm that it can provide substantial performance improvements over previous approaches.

Amortized Monte Carlo Integration

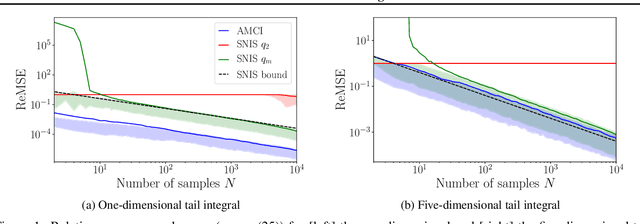
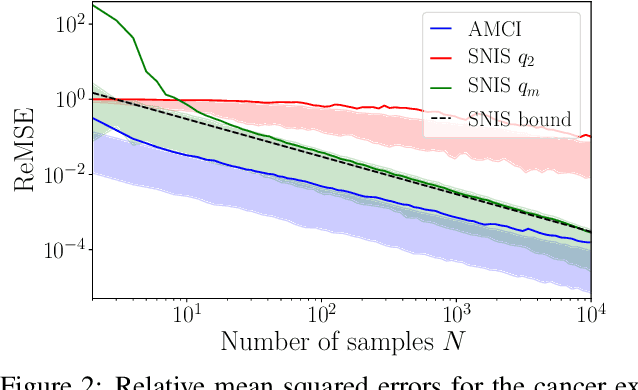
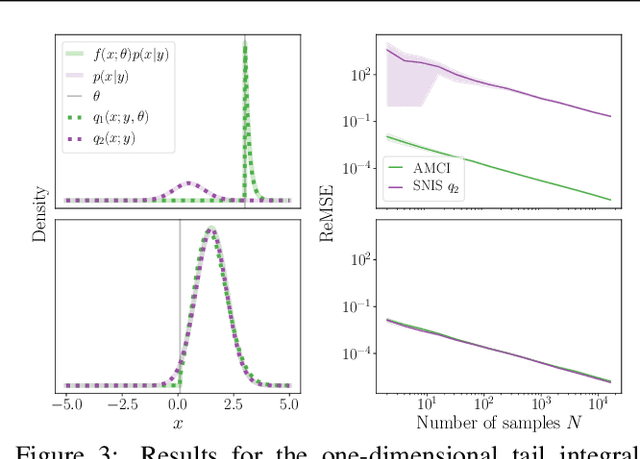
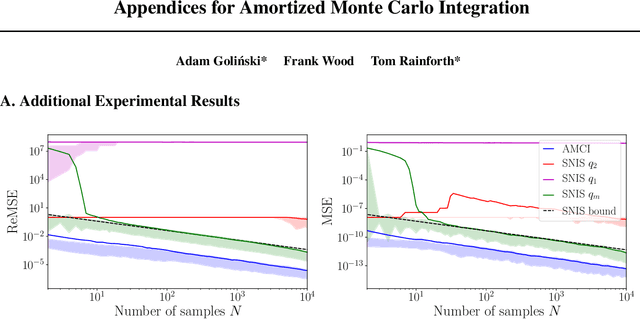
Current approaches to amortizing Bayesian inference focus solely on approximating the posterior distribution. Typically, this approximation is, in turn, used to calculate expectations for one or more target functions - a computational pipeline which is inefficient when the target function(s) are known upfront. In this paper, we address this inefficiency by introducing AMCI, a method for amortizing Monte Carlo integration directly. AMCI operates similarly to amortized inference but produces three distinct amortized proposals, each tailored to a different component of the overall expectation calculation. At runtime, samples are produced separately from each amortized proposal, before being combined to an overall estimate of the expectation. We show that while existing approaches are fundamentally limited in the level of accuracy they can achieve, AMCI can theoretically produce arbitrarily small errors for any integrable target function using only a single sample from each proposal at runtime. We further show that it is able to empirically outperform the theoretically optimal self-normalized importance sampler on a number of example problems. Furthermore, AMCI allows not only for amortizing over datasets but also amortizing over target functions.