Bayesian Neural Networks with Domain Knowledge Priors

Bayesian neural networks (BNNs) have recently gained popularity due to their ability to quantify model uncertainty. However, specifying a prior for BNNs that captures relevant domain knowledge is often extremely challenging. In this work, we propose a framework for integrating general forms of domain knowledge (i.e., any knowledge that can be represented by a loss function) into a BNN prior through variational inference, while enabling computationally efficient posterior inference and sampling. Specifically, our approach results in a prior over neural network weights that assigns high probability mass to models that better align with our domain knowledge, leading to posterior samples that also exhibit this behavior. We show that BNNs using our proposed domain knowledge priors outperform those with standard priors (e.g., isotropic Gaussian, Gaussian process), successfully incorporating diverse types of prior information such as fairness, physics rules, and healthcare knowledge and achieving better predictive performance. We also present techniques for transferring the learned priors across different model architectures, demonstrating their broad utility across various settings.

Spectrally Transformed Kernel Regression

Unlabeled data is a key component of modern machine learning. In general, the role of unlabeled data is to impose a form of smoothness, usually from the similarity information encoded in a base kernel, such as the $\epsilon$-neighbor kernel or the adjacency matrix of a graph. This work revisits the classical idea of spectrally transformed kernel regression (STKR), and provides a new class of general and scalable STKR estimators able to leverage unlabeled data. Intuitively, via spectral transformation, STKR exploits the data distribution for which unlabeled data can provide additional information. First, we show that STKR is a principled and general approach, by characterizing a universal type of "target smoothness", and proving that any sufficiently smooth function can be learned by STKR. Second, we provide scalable STKR implementations for the inductive setting and a general transformation function, while prior work is mostly limited to the transductive setting. Third, we derive statistical guarantees for two scenarios: STKR with a known polynomial transformation, and STKR with kernel PCA when the transformation is unknown. Overall, we believe that this work helps deepen our understanding of how to work with unlabeled data, and its generality makes it easier to inspire new methods.

Reliable Learning for Test-time Attacks and Distribution Shift

Machine learning algorithms are often used in environments which are not captured accurately even by the most carefully obtained training data, either due to the possibility of `adversarial' test-time attacks, or on account of `natural' distribution shift. For test-time attacks, we introduce and analyze a novel robust reliability guarantee, which requires a learner to output predictions along with a reliability radius $\eta$, with the meaning that its prediction is guaranteed to be correct as long as the adversary has not perturbed the test point farther than a distance $\eta$. We provide learners that are optimal in the sense that they always output the best possible reliability radius on any test point, and we characterize the reliable region, i.e. the set of points where a given reliability radius is attainable. We additionally analyze reliable learners under distribution shift, where the test points may come from an arbitrary distribution Q different from the training distribution P. For both cases, we bound the probability mass of the reliable region for several interesting examples, for linear separators under nearly log-concave and s-concave distributions, as well as for smooth boundary classifiers under smooth probability distributions.

Learning with Explanation Constraints

While supervised learning assumes the presence of labeled data, we may have prior information about how models should behave. In this paper, we formalize this notion as learning from explanation constraints and provide a learning theoretic framework to analyze how such explanations can improve the learning of our models. For what models would explanations be helpful? Our first key contribution addresses this question via the definition of what we call EPAC models (models that satisfy these constraints in expectation over new data), and we analyze this class of models using standard learning theoretic tools. Our second key contribution is to characterize these restrictions (in terms of their Rademacher complexities) for a canonical class of explanations given by gradient information for linear models and two layer neural networks. Finally, we provide an algorithmic solution for our framework, via a variational approximation that achieves better performance and satisfies these constraints more frequently, when compared to simpler augmented Lagrangian methods to incorporate these explanations. We demonstrate the benefits of our approach over a large array of synthetic and real-world experiments.

Nash Equilibria and Pitfalls of Adversarial Training in Adversarial Robustness Games

Adversarial training is a standard technique for training adversarially robust models. In this paper, we study adversarial training as an alternating best-response strategy in a 2-player zero-sum game. We prove that even in a simple scenario of a linear classifier and a statistical model that abstracts robust vs. non-robust features, the alternating best response strategy of such game may not converge. On the other hand, a unique pure Nash equilibrium of the game exists and is provably robust. We support our theoretical results with experiments, showing the non-convergence of adversarial training and the robustness of Nash equilibrium.

Label Propagation with Weak Supervision

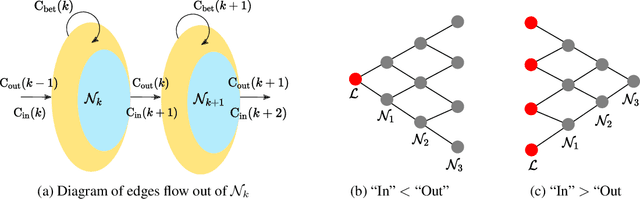
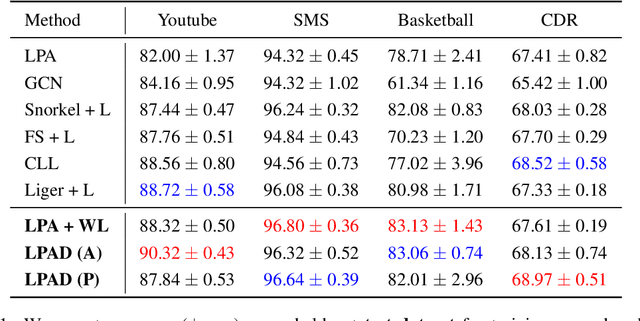
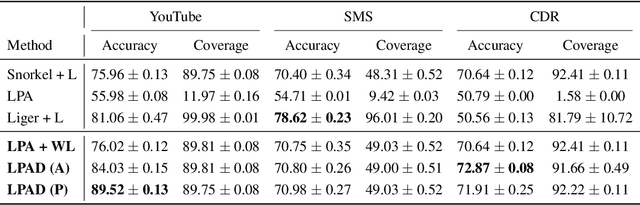
Semi-supervised learning and weakly supervised learning are important paradigms that aim to reduce the growing demand for labeled data in current machine learning applications. In this paper, we introduce a novel analysis of the classical label propagation algorithm (LPA) (Zhu & Ghahramani, 2002) that moreover takes advantage of useful prior information, specifically probabilistic hypothesized labels on the unlabeled data. We provide an error bound that exploits both the local geometric properties of the underlying graph and the quality of the prior information. We also propose a framework to incorporate multiple sources of noisy information. In particular, we consider the setting of weak supervision, where our sources of information are weak labelers. We demonstrate the ability of our approach on multiple benchmark weakly supervised classification tasks, showing improvements upon existing semi-supervised and weakly supervised methods.

Sharp asymptotics on the compression of two-layer neural networks

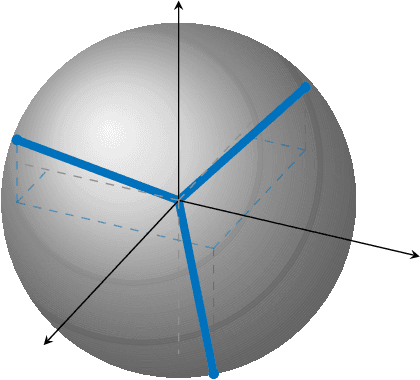
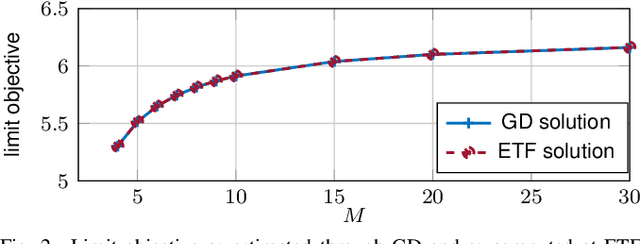
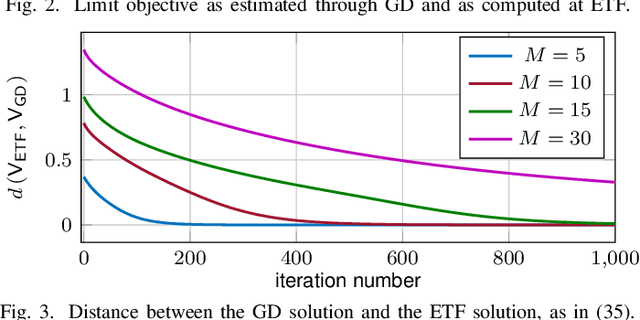
In this paper, we study the compression of a target two-layer neural network with N nodes into a compressed network with M < N nodes. More precisely, we consider the setting in which the weights of the target network are i.i.d. sub-Gaussian, and we minimize the population L2 loss between the outputs of the target and of the compressed network, under the assumption of Gaussian inputs. By using tools from high-dimensional probability, we show that this non-convex problem can be simplified when the target network is sufficiently over-parameterized, and provide the error rate of this approximation as a function of the input dimension and N . For a ReLU activation function, we conjecture that the optimum of the simplified optimization problem is achieved by taking weights on the Equiangular Tight Frame (ETF), while the scaling of the weights and the orientation of the ETF depend on the parameters of the target network. Numerical evidence is provided to support this conjecture.

Improving Transformation Invariance in Contrastive Representation Learning

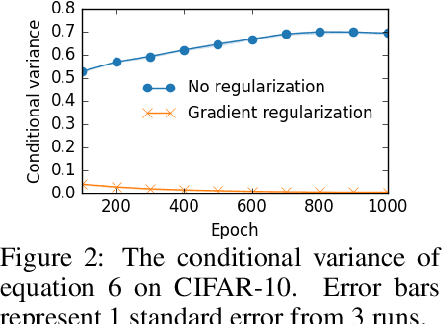
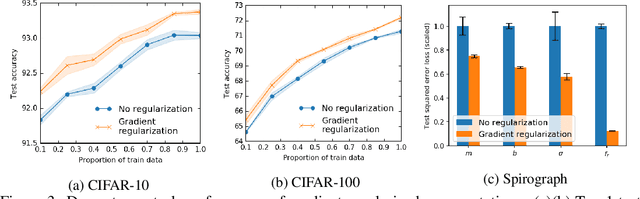
We propose methods to strengthen the invariance properties of representations obtained by contrastive learning. While existing approaches implicitly induce a degree of invariance as representations are learned, we look to more directly enforce invariance in the encoding process. To this end, we first introduce a training objective for contrastive learning that uses a novel regularizer to control how the representation changes under transformation. We show that representations trained with this objective perform better on downstream tasks and are more robust to the introduction of nuisance transformations at test time. Second, we propose a change to how test time representations are generated by introducing a feature averaging approach that combines encodings from multiple transformations of the original input, finding that this leads to across the board performance gains. Finally, we introduce the novel Spirograph dataset to explore our ideas in the context of a differentiable generative process with multiple downstream tasks, showing that our techniques for learning invariance are highly beneficial.