ERA: Expert Retrieval and Assembly for Early Action Prediction

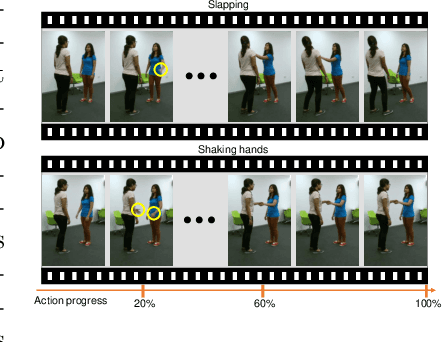
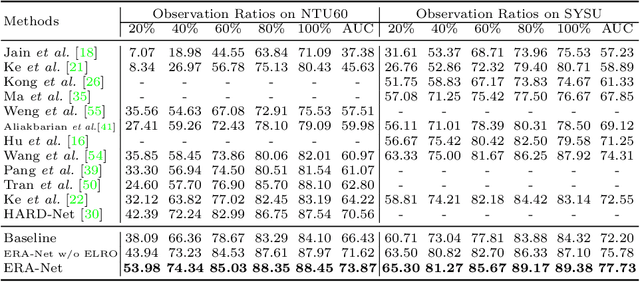
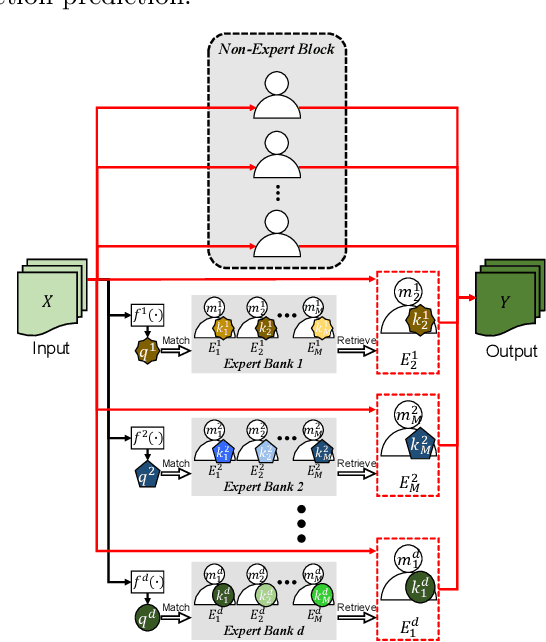
Early action prediction aims to successfully predict the class label of an action before it is completely performed. This is a challenging task because the beginning stages of different actions can be very similar, with only minor subtle differences for discrimination. In this paper, we propose a novel Expert Retrieval and Assembly (ERA) module that retrieves and assembles a set of experts most specialized at using discriminative subtle differences, to distinguish an input sample from other highly similar samples. To encourage our model to effectively use subtle differences for early action prediction, we push experts to discriminate exclusively between samples that are highly similar, forcing these experts to learn to use subtle differences that exist between those samples. Additionally, we design an effective Expert Learning Rate Optimization method that balances the experts' optimization and leads to better performance. We evaluate our ERA module on four public action datasets and achieve state-of-the-art performance.

Stochastic first-order methods for average-reward Markov decision processes

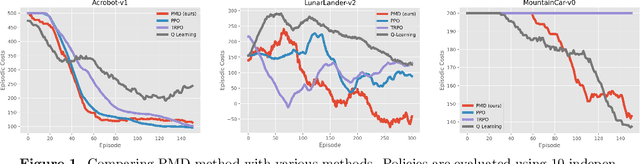
We study the problem of average-reward Markov decision processes (AMDPs) and develop novel first-order methods with strong theoretical guarantees for both policy evaluation and optimization. Existing on-policy evaluation methods suffer from sub-optimal convergence rates as well as failure in handling insufficiently random policies, e.g., deterministic policies, for lack of exploration. To remedy these issues, we develop a novel variance-reduced temporal difference (VRTD) method with linear function approximation for randomized policies along with optimal convergence guarantees, and an exploratory variance-reduced temporal difference (EVRTD) method for insufficiently random policies with comparable convergence guarantees. We further establish linear convergence rate on the bias of policy evaluation, which is essential for improving the overall sample complexity of policy optimization. On the other hand, compared with intensive research interest in finite sample analysis of policy gradient methods for discounted MDPs, existing studies on policy gradient methods for AMDPs mostly focus on regret bounds under restrictive assumptions on the underlying Markov processes (see, e.g., Abbasi-Yadkori et al., 2019), and they often lack guarantees on the overall sample complexities. Towards this end, we develop an average-reward variant of the stochastic policy mirror descent (SPMD) (Lan, 2022). We establish the first $\widetilde{\mathcal{O}}(\epsilon^{-2})$ sample complexity for solving AMDPs with policy gradient method under both the generative model (with unichain assumption) and Markovian noise model (with ergodic assumption). This bound can be further improved to $\widetilde{\mathcal{O}}(\epsilon^{-1})$ for solving regularized AMDPs. Our theoretical advantages are corroborated by numerical experiments.

Accelerated and instance-optimal policy evaluation with linear function approximation

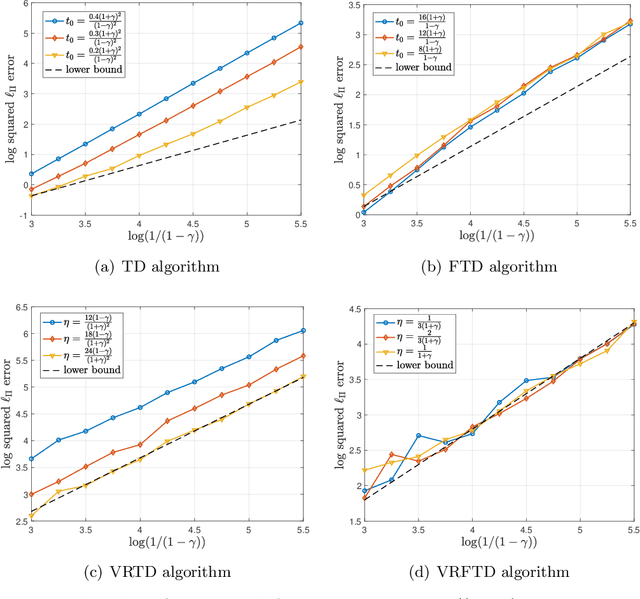
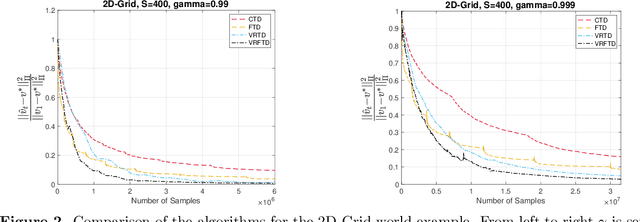
We study the problem of policy evaluation with linear function approximation and present efficient and practical algorithms that come with strong optimality guarantees. We begin by proving lower bounds that establish baselines on both the deterministic error and stochastic error in this problem. In particular, we prove an oracle complexity lower bound on the deterministic error in an instance-dependent norm associated with the stationary distribution of the transition kernel, and use the local asymptotic minimax machinery to prove an instance-dependent lower bound on the stochastic error in the i.i.d. observation model. Existing algorithms fail to match at least one of these lower bounds: To illustrate, we analyze a variance-reduced variant of temporal difference learning, showing in particular that it fails to achieve the oracle complexity lower bound. To remedy this issue, we develop an accelerated, variance-reduced fast temporal difference algorithm (VRFTD) that simultaneously matches both lower bounds and attains a strong notion of instance-optimality. Finally, we extend the VRFTD algorithm to the setting with Markovian observations, and provide instance-dependent convergence results that match those in the i.i.d. setting up to a multiplicative factor that is proportional to the mixing time of the chain. Our theoretical guarantees of optimality are corroborated by numerical experiments.

Faster Algorithm and Sharper Analysis for Constrained Markov Decision Process

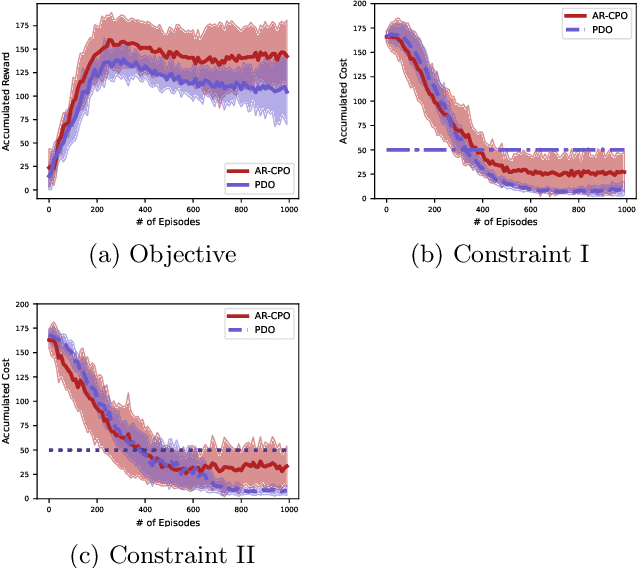
The problem of constrained Markov decision process (CMDP) is investigated, where an agent aims to maximize the expected accumulated discounted reward subject to multiple constraints on its utilities/costs. A new primal-dual approach is proposed with a novel integration of three ingredients: entropy regularized policy optimizer, dual variable regularizer, and Nesterov's accelerated gradient descent dual optimizer, all of which are critical to achieve a faster convergence. The finite-time error bound of the proposed approach is characterized. Despite the challenge of the nonconcave objective subject to nonconcave constraints, the proposed approach is shown to converge to the global optimum with a complexity of $\tilde{\mathcal O}(1/\epsilon)$ in terms of the optimality gap and the constraint violation, which improves the complexity of the existing primal-dual approach by a factor of $\mathcal O(1/\epsilon)$ \citep{ding2020natural,paternain2019constrained}. This is the first demonstration that nonconcave CMDP problems can attain the complexity lower bound of $\mathcal O(1/\epsilon)$ for convex optimization subject to convex constraints. Our primal-dual approach and non-asymptotic analysis are agnostic to the RL optimizer used, and thus are more flexible for practical applications. More generally, our approach also serves as the first algorithm that provably accelerates constrained nonconvex optimization with zero duality gap by exploiting the geometries such as the gradient dominance condition, for which the existing acceleration methods for constrained convex optimization are not applicable.

The Multi-Modal Video Reasoning and Analyzing Competition

In this paper, we introduce the Multi-Modal Video Reasoning and Analyzing Competition (MMVRAC) workshop in conjunction with ICCV 2021. This competition is composed of four different tracks, namely, video question answering, skeleton-based action recognition, fisheye video-based action recognition, and person re-identification, which are based on two datasets: SUTD-TrafficQA and UAV-Human. We summarize the top-performing methods submitted by the participants in this competition and show their results achieved in the competition.

UAV-Human: A Large Benchmark for Human Behavior Understanding with Unmanned Aerial Vehicles

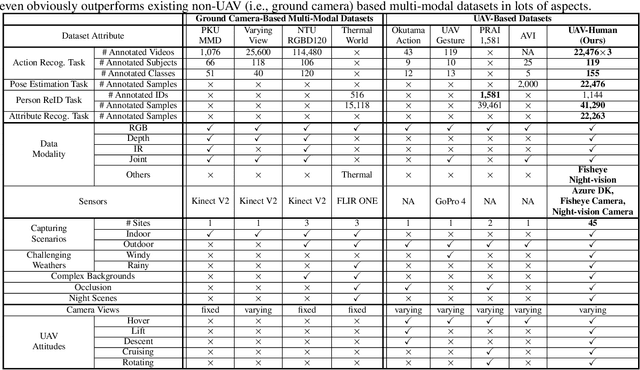
Human behavior understanding with unmanned aerial vehicles (UAVs) is of great significance for a wide range of applications, which simultaneously brings an urgent demand of large, challenging, and comprehensive benchmarks for the development and evaluation of UAV-based models. However, existing benchmarks have limitations in terms of the amount of captured data, types of data modalities, categories of provided tasks, and diversities of subjects and environments. Here we propose a new benchmark - UAVHuman - for human behavior understanding with UAVs, which contains 67,428 multi-modal video sequences and 119 subjects for action recognition, 22,476 frames for pose estimation, 41,290 frames and 1,144 identities for person re-identification, and 22,263 frames for attribute recognition. Our dataset was collected by a flying UAV in multiple urban and rural districts in both daytime and nighttime over three months, hence covering extensive diversities w.r.t subjects, backgrounds, illuminations, weathers, occlusions, camera motions, and UAV flying attitudes. Such a comprehensive and challenging benchmark shall be able to promote the research of UAV-based human behavior understanding, including action recognition, pose estimation, re-identification, and attribute recognition. Furthermore, we propose a fisheye-based action recognition method that mitigates the distortions in fisheye videos via learning unbounded transformations guided by flat RGB videos. Experiments show the efficacy of our method on the UAV-Human dataset. The project page: https://github.com/SUTDCV/UAV-Human

Simple and optimal methods for stochastic variational inequalities, II: Markovian noise and policy evaluation in reinforcement learning

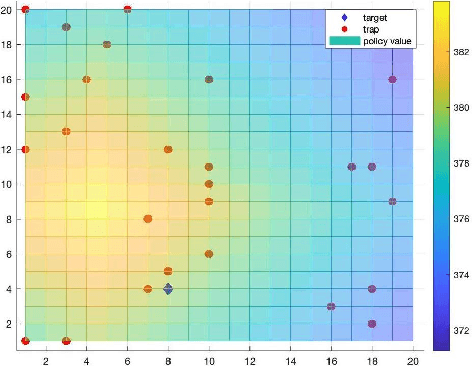
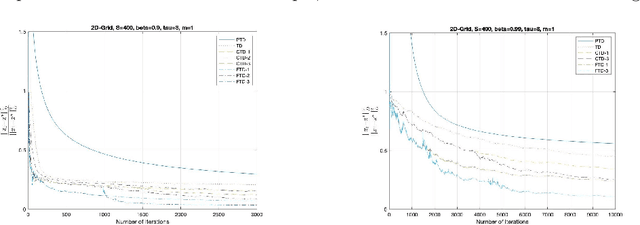
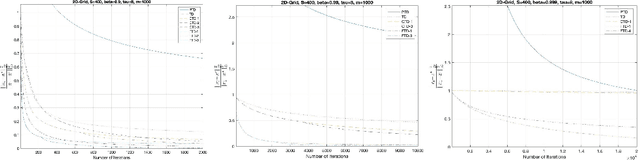
The focus of this paper is on stochastic variational inequalities (VI) under Markovian noise. A prominent application of our algorithmic developments is the stochastic policy evaluation problem in reinforcement learning. Prior investigations in the literature focused on temporal difference (TD) learning by employing nonsmooth finite time analysis motivated by stochastic subgradient descent leading to certain limitations. These encompass the requirement of analyzing a modified TD algorithm that involves projection to an a-priori defined Euclidean ball, achieving a non-optimal convergence rate and no clear way of deriving the beneficial effects of parallel implementation. Our approach remedies these shortcomings in the broader context of stochastic VIs and in particular when it comes to stochastic policy evaluation. We developed a variety of simple TD learning type algorithms motivated by its original version that maintain its simplicity, while offering distinct advantages from a non-asymptotic analysis point of view. We first provide an improved analysis of the standard TD algorithm that can benefit from parallel implementation. Then we present versions of a conditional TD algorithm (CTD), that involves periodic updates of the stochastic iterates, which reduce the bias and therefore exhibit improved iteration complexity. This brings us to the fast TD (FTD) algorithm which combines elements of CTD and the stochastic operator extrapolation method of the companion paper. For a novel index resetting policy FTD exhibits the best known convergence rate. We also devised a robust version of the algorithm that is particularly suitable for discounting factors close to 1.

Simple and optimal methods for stochastic variational inequalities, I: operator extrapolation

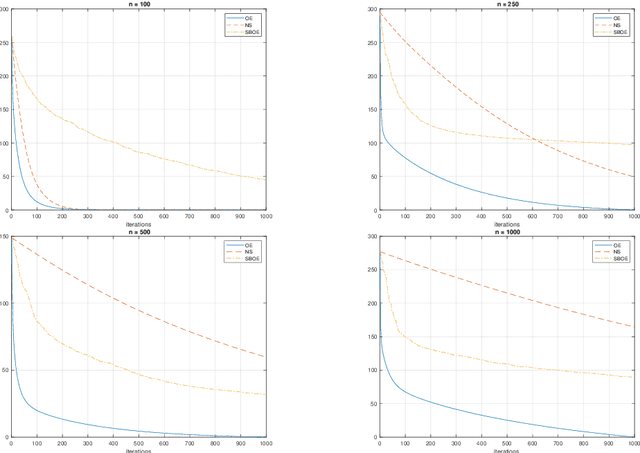
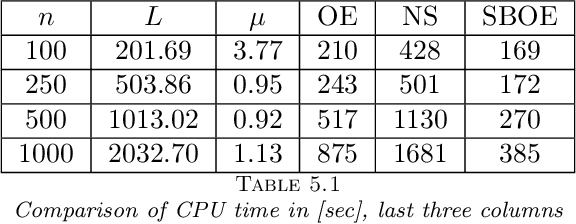
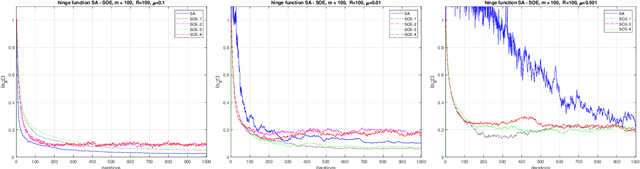
In this paper we first present a novel operator extrapolation (OE) method for solving deterministic variational inequality (VI) problems. Similar to the gradient (operator) projection method, OE updates one single search sequence by solving a single projection subproblem in each iteration. We show that OE can achieve the optimal rate of convergence for solving a variety of VI problems in a much simpler way than existing approaches. We then introduce the stochastic operator extrapolation (SOE) method and establish its optimal convergence behavior for solving different stochastic VI problems. In particular, SOE achieves the optimal complexity for solving a fundamental problem, i.e., stochastic smooth and strongly monotone VI, for the first time in the literature. We also present a stochastic block operator extrapolations (SBOE) method to further reduce the iteration cost for the OE method applied to large-scale deterministic VIs with a certain block structure. Numerical experiments have been conducted to demonstrate the potential advantages of the proposed algorithms. In fact, all these algorithms are applied to solve generalized monotone variational inequality (GMVI) problems whose operator is not necessarily monotone. We will also discuss optimal OE-based policy evaluation methods for reinforcement learning in a companion paper.