Simple and optimal methods for stochastic variational inequalities, II: Markovian noise and policy evaluation in reinforcement learning

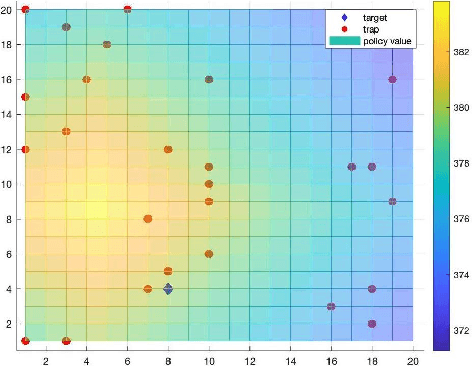
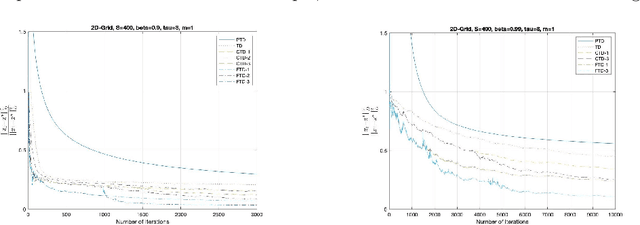
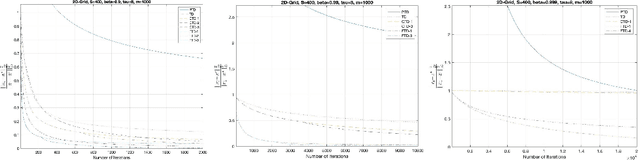
The focus of this paper is on stochastic variational inequalities (VI) under Markovian noise. A prominent application of our algorithmic developments is the stochastic policy evaluation problem in reinforcement learning. Prior investigations in the literature focused on temporal difference (TD) learning by employing nonsmooth finite time analysis motivated by stochastic subgradient descent leading to certain limitations. These encompass the requirement of analyzing a modified TD algorithm that involves projection to an a-priori defined Euclidean ball, achieving a non-optimal convergence rate and no clear way of deriving the beneficial effects of parallel implementation. Our approach remedies these shortcomings in the broader context of stochastic VIs and in particular when it comes to stochastic policy evaluation. We developed a variety of simple TD learning type algorithms motivated by its original version that maintain its simplicity, while offering distinct advantages from a non-asymptotic analysis point of view. We first provide an improved analysis of the standard TD algorithm that can benefit from parallel implementation. Then we present versions of a conditional TD algorithm (CTD), that involves periodic updates of the stochastic iterates, which reduce the bias and therefore exhibit improved iteration complexity. This brings us to the fast TD (FTD) algorithm which combines elements of CTD and the stochastic operator extrapolation method of the companion paper. For a novel index resetting policy FTD exhibits the best known convergence rate. We also devised a robust version of the algorithm that is particularly suitable for discounting factors close to 1.

Simple and optimal methods for stochastic variational inequalities, I: operator extrapolation

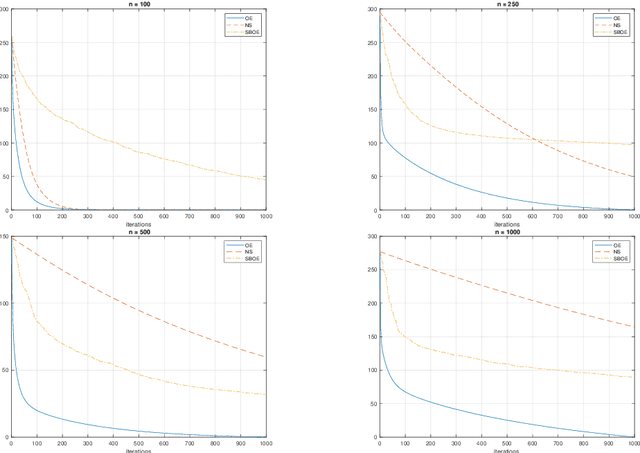
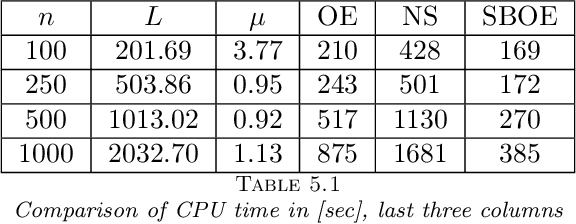
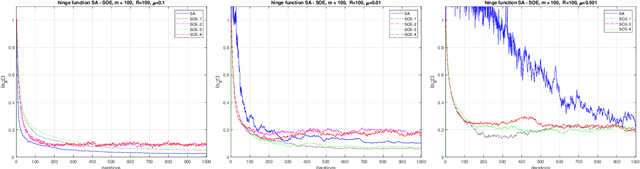
In this paper we first present a novel operator extrapolation (OE) method for solving deterministic variational inequality (VI) problems. Similar to the gradient (operator) projection method, OE updates one single search sequence by solving a single projection subproblem in each iteration. We show that OE can achieve the optimal rate of convergence for solving a variety of VI problems in a much simpler way than existing approaches. We then introduce the stochastic operator extrapolation (SOE) method and establish its optimal convergence behavior for solving different stochastic VI problems. In particular, SOE achieves the optimal complexity for solving a fundamental problem, i.e., stochastic smooth and strongly monotone VI, for the first time in the literature. We also present a stochastic block operator extrapolations (SBOE) method to further reduce the iteration cost for the OE method applied to large-scale deterministic VIs with a certain block structure. Numerical experiments have been conducted to demonstrate the potential advantages of the proposed algorithms. In fact, all these algorithms are applied to solve generalized monotone variational inequality (GMVI) problems whose operator is not necessarily monotone. We will also discuss optimal OE-based policy evaluation methods for reinforcement learning in a companion paper.