Detecting Changes in Asset Co-Movement Using the Autoencoder Reconstruction Ratio

Detecting changes in asset co-movements is of much importance to financial practitioners, with numerous risk management benefits arising from the timely detection of breakdowns in historical correlations. In this article, we propose a real-time indicator to detect temporary increases in asset co-movements, the Autoencoder Reconstruction Ratio, which measures how well a basket of asset returns can be modelled using a lower-dimensional set of latent variables. The ARR uses a deep sparse denoising autoencoder to perform the dimensionality reduction on the returns vector, which replaces the PCA approach of the standard Absorption Ratio, and provides a better model for non-Gaussian returns. Through a systemic risk application on forecasting on the CRSP US Total Market Index, we show that lower ARR values coincide with higher volatility and larger drawdowns, indicating that increased asset co-movement does correspond with periods of market weakness. We also demonstrate that short-term (i.e. 5-min and 1-hour) predictors for realised volatility and market crashes can be improved by including additional ARR inputs.

Safety Guarantees for Planning Based on Iterative Gaussian Processes

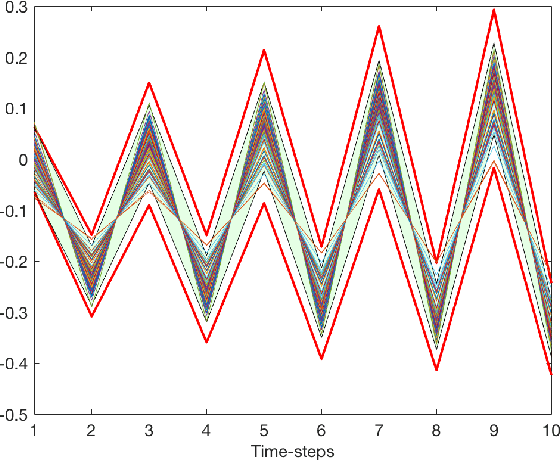
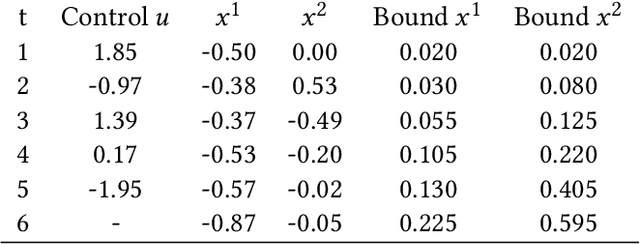
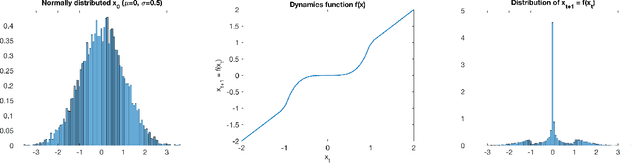
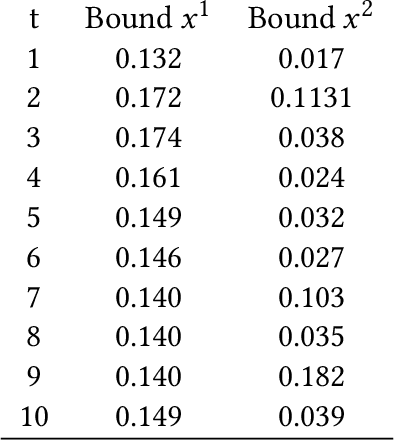
Gaussian Processes (GPs) are widely employed in control and learning because of their principled treatment of uncertainty. However, tracking uncertainty for iterative, multi-step predictions in general leads to an analytically intractable problem. While approximation methods exist, they do not come with guarantees, making it difficult to estimate their reliability and to trust their predictions. In this work, we derive formal probability error bounds for iterative prediction and planning with GPs. Building on GP properties, we bound the probability that random trajectories lie in specific regions around the predicted values. Namely, given a tolerance $\epsilon > 0 $, we compute regions around the predicted trajectory values, such that GP trajectories are guaranteed to lie inside them with probability at least $1-\epsilon$. We verify experimentally that our method tracks the predictive uncertainty correctly, even when current approximation techniques fail. Furthermore, we show how the proposed bounds can be employed within a safe reinforcement learning framework to verify the safety of candidate control policies, guiding the synthesis of provably safe controllers.

MLRG Deep Curvature

We present MLRG Deep Curvature suite, a PyTorch-based, open-source package for analysis and visualisation of neural network curvature and loss landscape. Despite of providing rich information into properties of neural network and useful for a various designed tasks, curvature information is still not made sufficient use for various reasons, and our method aims to bridge this gap. We present a primer, including its main practical desiderata and common misconceptions, of \textit{Lanczos algorithm}, the theoretical backbone of our package, and present a series of examples based on synthetic toy examples and realistic modern neural networks tested on CIFAR datasets, and show the superiority of our package against existing competing approaches for the similar purposes.

A Maximum Entropy approach to Massive Graph Spectra

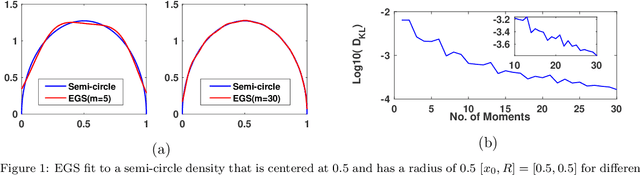
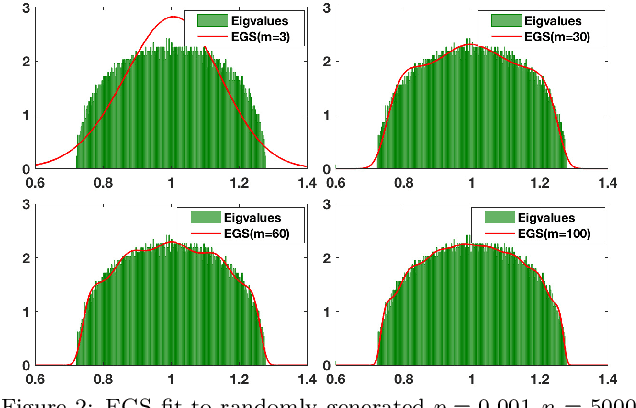
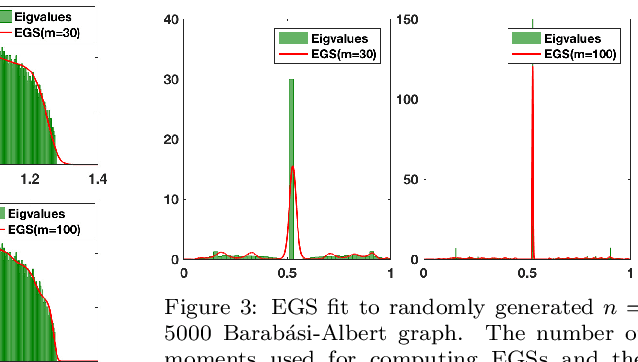
Graph spectral techniques for measuring graph similarity, or for learning the cluster number, require kernel smoothing. The choice of kernel function and bandwidth are typically chosen in an ad-hoc manner and heavily affect the resulting output. We prove that kernel smoothing biases the moments of the spectral density. We propose an information theoretically optimal approach to learn a smooth graph spectral density, which fully respects the moment information. Our method's computational cost is linear in the number of edges, and hence can be applied to large networks, with millions of nodes. We apply our method to the problems to graph similarity and cluster number learning, where we outperform comparable iterative spectral approaches on synthetic and real graphs.

Indian Buffet Neural Networks for Continual Learning

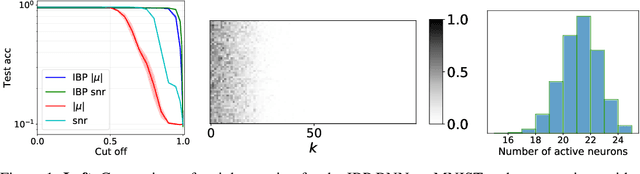
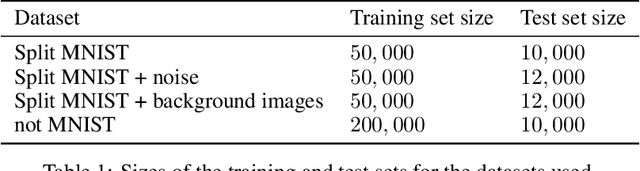
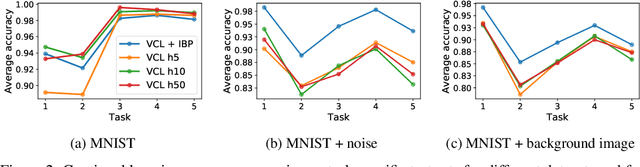
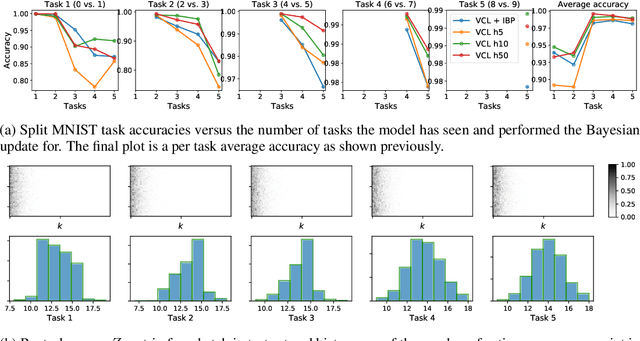
We place an Indian Buffet Process (IBP) prior over the neural structure of a Bayesian Neural Network (BNN), thus allowing the complexity of the BNN to increase and decrease automatically. We apply this methodology to the problem of resource allocation in continual learning, where new tasks occur and the network requires extra resources. Our BNN exploits online variational inference with relaxations to the Bernoulli and Beta distributions (which constitute the IBP prior), so allowing the use of the reparameterisation trick to learn variational posteriors via gradient-based methods. As we automatically learn the number of weights in the BNN, overfitting and underfitting problems are largely overcome. We show empirically that the method offers competitive results compared to Variational Continual Learning (VCL) in some settings.

Deep Reinforcement Learning for Trading

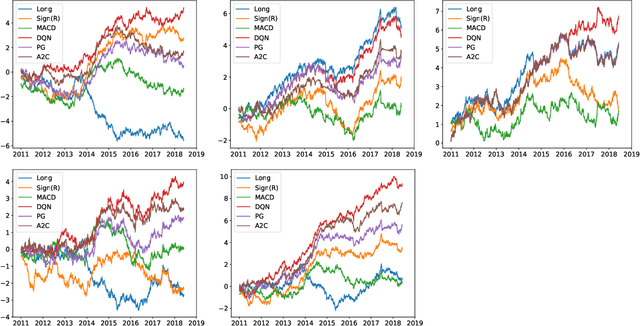
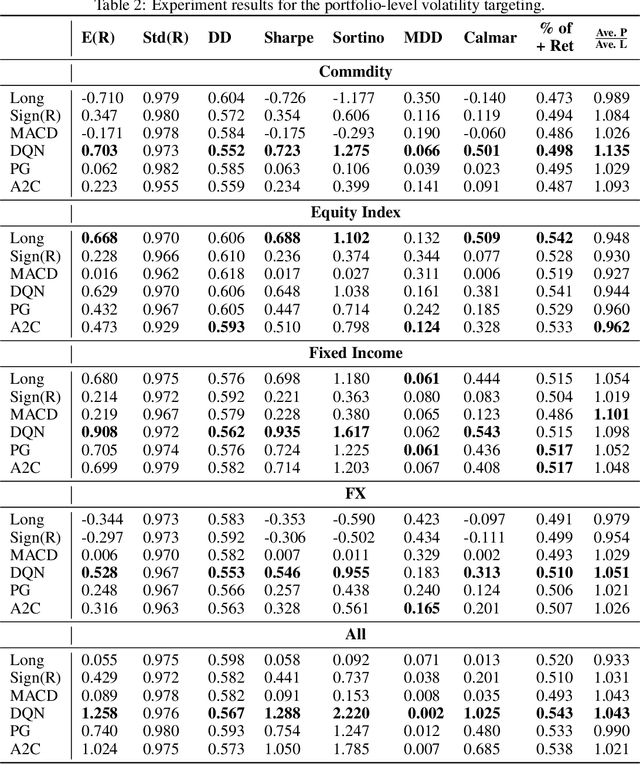
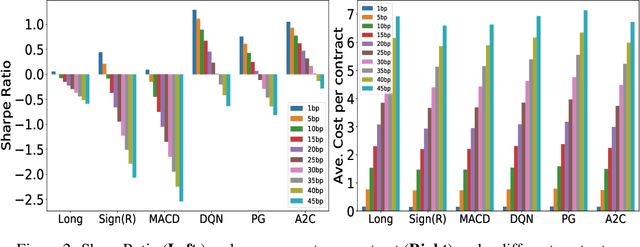
We adopt Deep Reinforcement Learning algorithms to design trading strategies for continuous futures contracts. Both discrete and continuous action spaces are considered and volatility scaling is incorporated to create reward functions which scale trade positions based on market volatility. We test our algorithms on the 50 most liquid futures contracts from 2011 to 2019, and investigate how performance varies across different asset classes including commodities, equity indices, fixed income and FX markets. We compare our algorithms against classical time series momentum strategies, and show that our method outperforms such baseline models, delivering positive profits despite heavy transaction costs. The experiments show that the proposed algorithms can follow large market trends without changing positions and can also scale down, or hold, through consolidation periods.

Regularising Deep Networks with Deep Generative Models

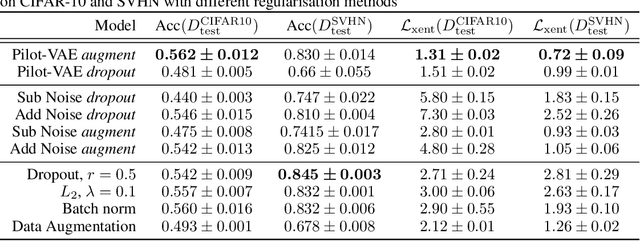
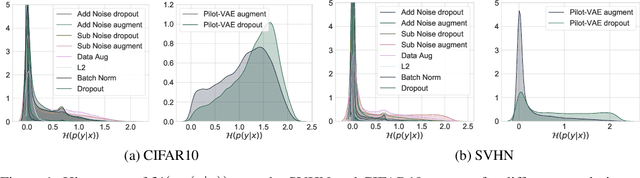
We develop a new method for regularising neural networks. We learn a probability distribution over the activations of all layers of the model and then insert imputed values into the network during training. We obtain a posterior for an arbitrary subset of activations conditioned on the remainder. This is a generalisation of data augmentation to the hidden layers of a network, and a form of data-aware dropout. We demonstrate that our training method leads to higher test accuracy and lower test-set cross-entropy for neural networks trained on CIFAR-10 and SVHN compared to standard regularisation baselines: our approach leads to networks with better calibrated uncertainty over the class posteriors all the while delivering greater test-set accuracy.

Disentangling to Cluster: Gaussian Mixture Variational Ladder Autoencoders

In clustering we normally output one cluster variable for each datapoint. However it is not necessarily the case that there is only one way to partition a given dataset into cluster components. For example, one could cluster objects by their colour, or by their type. Different attributes form a hierarchy, and we could wish to cluster in any of them. By disentangling the learnt latent representations of some dataset into different layers for different attributes we can then cluster in those latent spaces. We call this "disentangled clustering". Extending Variational Ladder Autoencoders (Zhao et al., 2017), we propose a clustering algorithm, VLAC, that outperforms a Gaussian Mixture DGM in cluster accuracy over digit identity on the test set of SVHN. We also demonstrate learning clusters jointly over numerous layers of the hierarchy of latent variables for the data, and show component-wise generation from this hierarchical model.

Balancing Reconstruction Quality and Regularisation in ELBO for VAEs

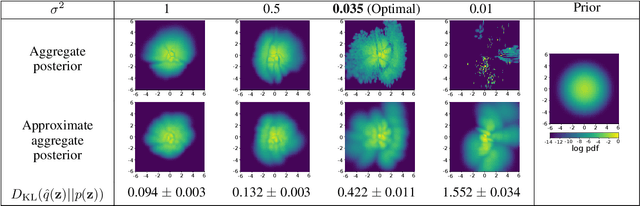
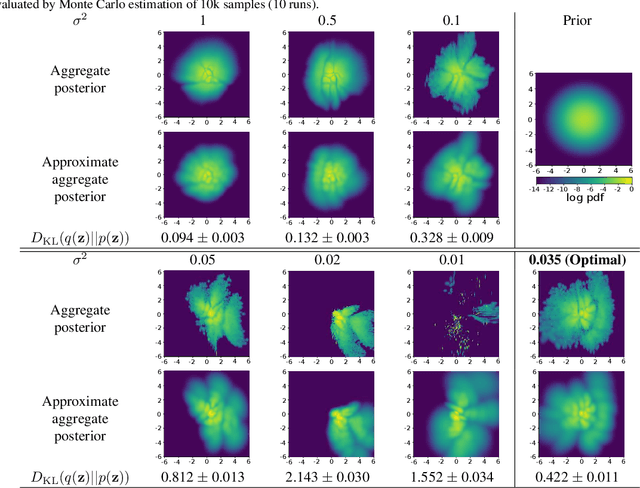
A trade-off exists between reconstruction quality and the prior regularisation in the Evidence Lower Bound (ELBO) loss that Variational Autoencoder (VAE) models use for learning. There are few satisfactory approaches to deal with a balance between the prior and reconstruction objective, with most methods dealing with this problem through heuristics. In this paper, we show that the noise variance (often set as a fixed value) in the Gaussian likelihood p(x|z) for real-valued data can naturally act to provide such a balance. By learning this noise variance so as to maximise the ELBO loss, we automatically obtain an optimal trade-off between the reconstruction error and the prior constraint on the posteriors. This variance can be interpreted intuitively as the necessary noise level for the current model to be the best explanation of the observed dataset. Further, by allowing the variance inference to be more flexible it can conveniently be used as an uncertainty estimator for reconstructed or generated samples. We demonstrate that optimising the noise variance is a crucial component of VAE learning, and showcase the performance on MNIST, Fashion MNIST and CelebA datasets. We find our approach can significantly improve the quality of generated samples whilst maintaining a smooth latent-space manifold to represent the data. The method also offers an indication of uncertainty in the final generative model.

MEMe: An Accurate Maximum Entropy Method for Efficient Approximations in Large-Scale Machine Learning

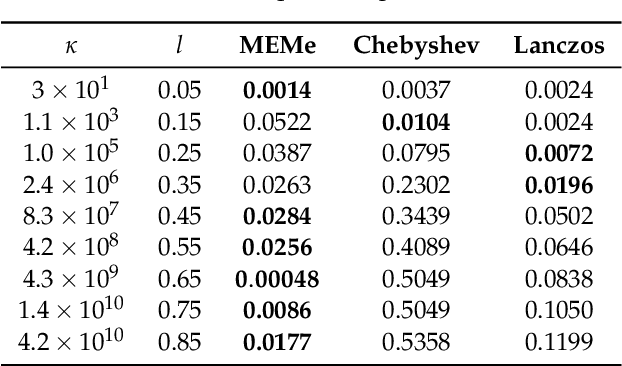
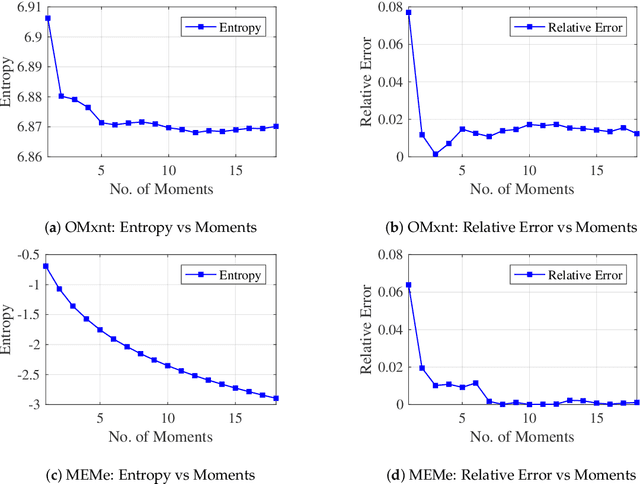
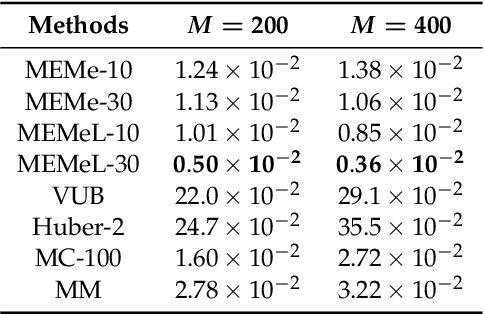
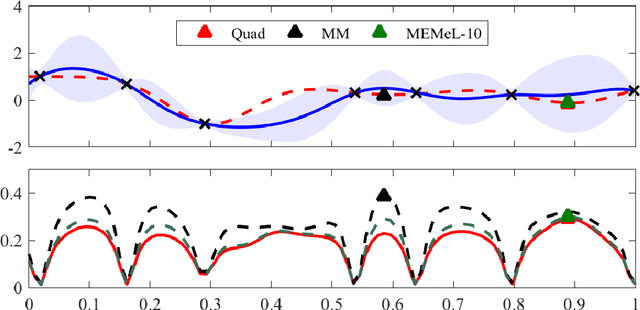
Efficient approximation lies at the heart of large-scale machine learning problems. In this paper, we propose a novel, robust maximum entropy algorithm, which is capable of dealing with hundreds of moments and allows for computationally efficient approximations. We showcase the usefulness of the proposed method, its equivalence to constrained Bayesian variational inference and demonstrate its superiority over existing approaches in two applications, namely, fast log determinant estimation and information-theoretic Bayesian optimisation.