Bayesian Quadrature for Neural Ensemble Search

Ensembling can improve the performance of Neural Networks, but existing approaches struggle when the architecture likelihood surface has dispersed, narrow peaks. Furthermore, existing methods construct equally weighted ensembles, and this is likely to be vulnerable to the failure modes of the weaker architectures. By viewing ensembling as approximately marginalising over architectures we construct ensembles using the tools of Bayesian Quadrature -- tools which are well suited to the exploration of likelihood surfaces with dispersed, narrow peaks. Additionally, the resulting ensembles consist of architectures weighted commensurate with their performance. We show empirically -- in terms of test likelihood, accuracy, and expected calibration error -- that our method outperforms state-of-the-art baselines, and verify via ablation studies that its components do so independently.

Neural Architecture Search using Bayesian Optimisation with Weisfeiler-Lehman Kernel

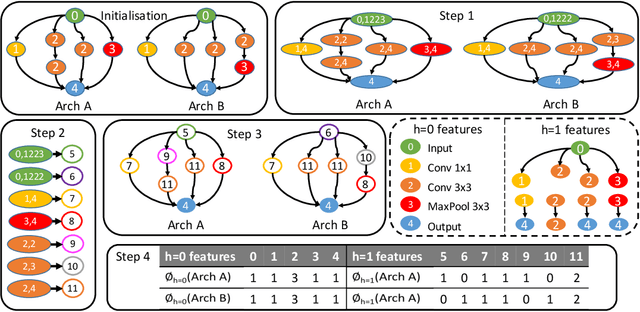
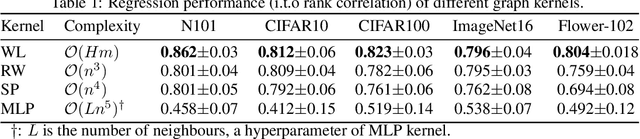
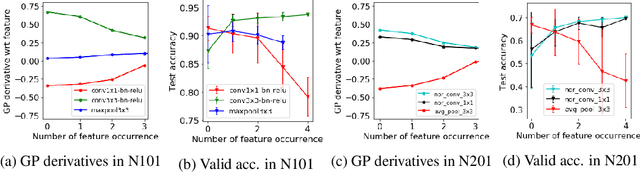
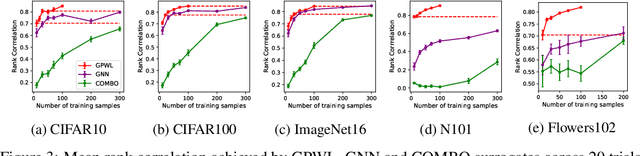
Bayesian optimisation (BO) has been widely used for hyperparameter optimisation but its application in neural architecture search (NAS) is limited due to the non-continuous, high-dimensional and graph-like search spaces. Current approaches either rely on encoding schemes, which are not scalable to large architectures and ignore the implicit topological structure of architectures, or use graph neural networks, which require additional hyperparameter tuning and a large amount of observed data, which is particularly expensive to obtain in NAS. We propose a neat BO approach for NAS, which combines the Weisfeiler-Lehman graph kernel with a Gaussian process surrogate to capture the topological structure of architectures, without having to explicitly define a Gaussian process over high-dimensional vector spaces. We also harness the interpretable features learnt via the graph kernel to guide the generation of new architectures. We demonstrate empirically that our surrogate model is scalable to large architectures and highly data-efficient; competing methods require 3 to 20 times more observations to achieve equally good prediction performance as ours. We finally show that our method outperforms existing NAS approaches to achieve state-of-the-art results on NAS datasets.

A Maximum Entropy approach to Massive Graph Spectra

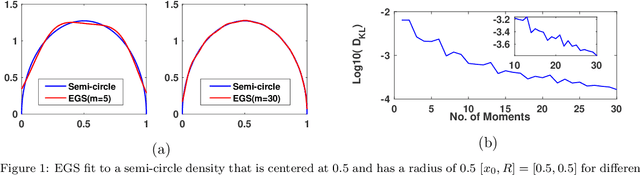
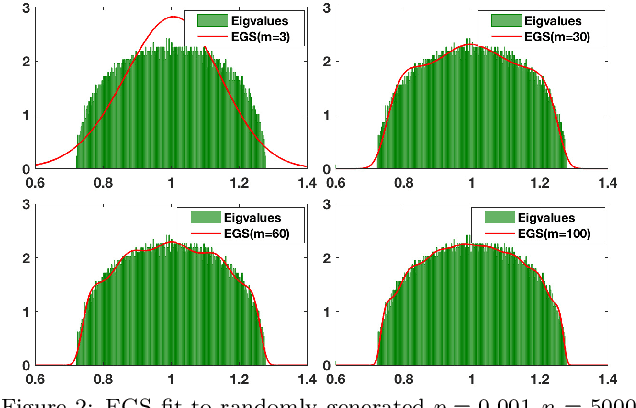
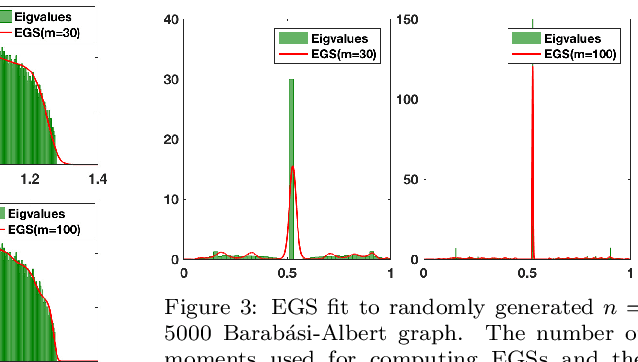
Graph spectral techniques for measuring graph similarity, or for learning the cluster number, require kernel smoothing. The choice of kernel function and bandwidth are typically chosen in an ad-hoc manner and heavily affect the resulting output. We prove that kernel smoothing biases the moments of the spectral density. We propose an information theoretically optimal approach to learn a smooth graph spectral density, which fully respects the moment information. Our method's computational cost is linear in the number of edges, and hence can be applied to large networks, with millions of nodes. We apply our method to the problems to graph similarity and cluster number learning, where we outperform comparable iterative spectral approaches on synthetic and real graphs.

Radial Bayesian Neural Networks: Robust Variational Inference In Big Models

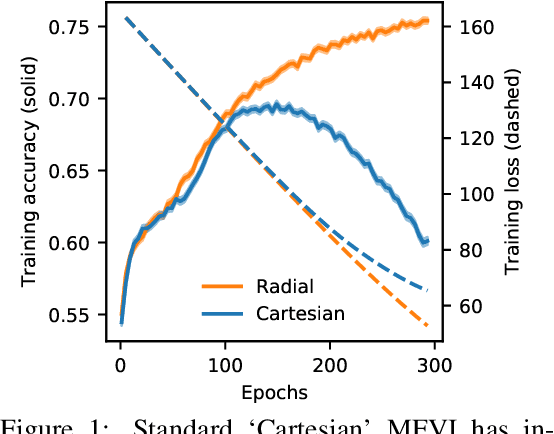
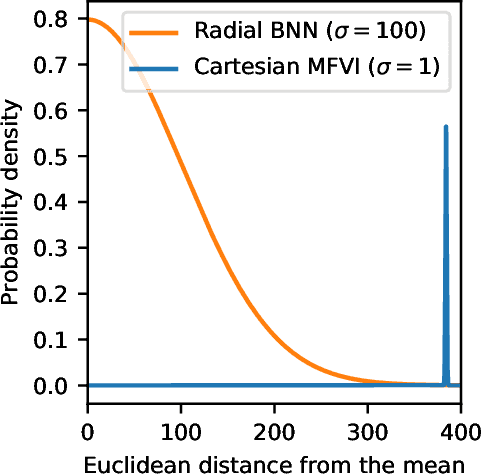
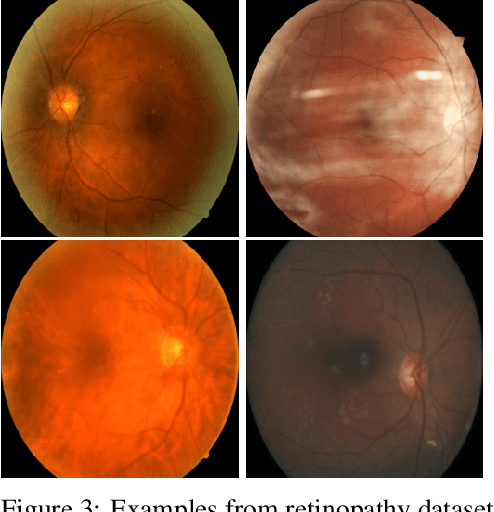
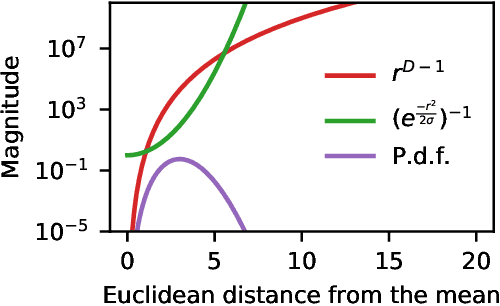
We propose Radial Bayesian Neural Networks: a variational distribution for mean field variational inference (MFVI) in Bayesian neural networks that is simple to implement, scalable to large models, and robust to hyperparameter selection. We hypothesize that standard MFVI fails in large models because of a property of the high-dimensional Gaussians used as posteriors. As variances grow, samples come almost entirely from a `soap-bubble' far from the mean. We show that the ad-hoc tweaks used previously in the literature to get MFVI to work served to stop such variances growing. Designing a new posterior distribution, we avoid this pathology in a theoretically principled way. Our distribution improves accuracy and uncertainty over standard MFVI, while scaling to large data where most other VI and MCMC methods struggle. We benchmark Radial BNNs in a real-world task of diabetic retinopathy diagnosis from fundus images, a task with ~100x larger input dimensionality and model size compared to previous demonstrations of MFVI.

MEMe: An Accurate Maximum Entropy Method for Efficient Approximations in Large-Scale Machine Learning

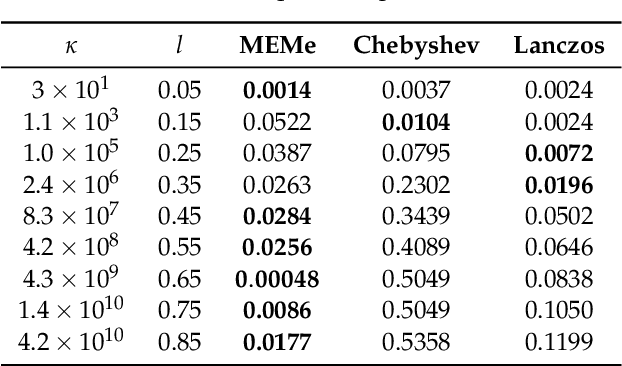
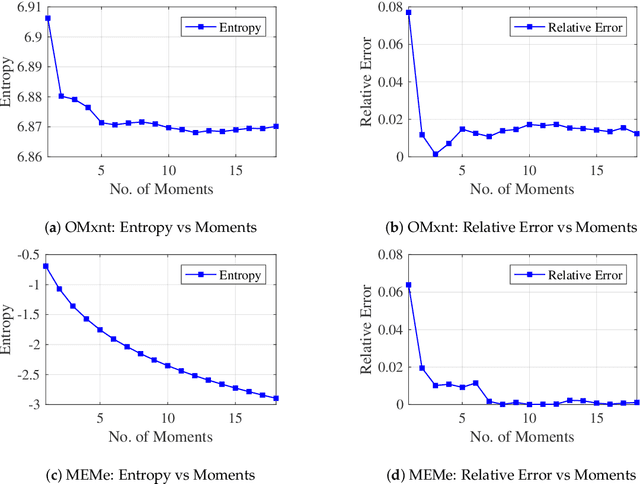
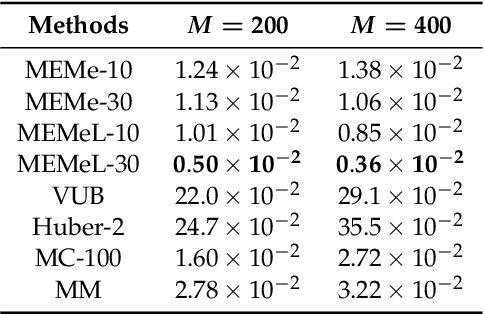
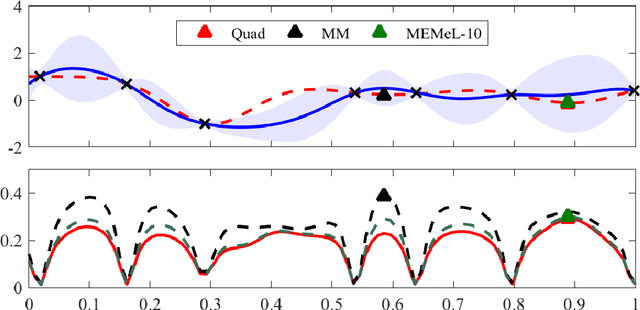
Efficient approximation lies at the heart of large-scale machine learning problems. In this paper, we propose a novel, robust maximum entropy algorithm, which is capable of dealing with hundreds of moments and allows for computationally efficient approximations. We showcase the usefulness of the proposed method, its equivalence to constrained Bayesian variational inference and demonstrate its superiority over existing approaches in two applications, namely, fast log determinant estimation and information-theoretic Bayesian optimisation.

On the Limitations of Representing Functions on Sets

Recent work on the representation of functions on sets has considered the use of summation in a latent space to enforce permutation invariance. In particular, it has been conjectured that the dimension of this latent space may remain fixed as the cardinality of the sets under consideration increases. However, we demonstrate that the analysis leading to this conjecture requires mappings which are highly discontinuous and argue that this is only of limited practical use. Motivated by this observation, we prove that an implementation of this model via continuous mappings (as provided by e.g. neural networks or Gaussian processes) actually imposes a constraint on the dimensionality of the latent space. Practical universal function representation for set inputs can only be achieved with a latent dimension at least the size of the maximum number of input elements.

Batch Selection for Parallelisation of Bayesian Quadrature

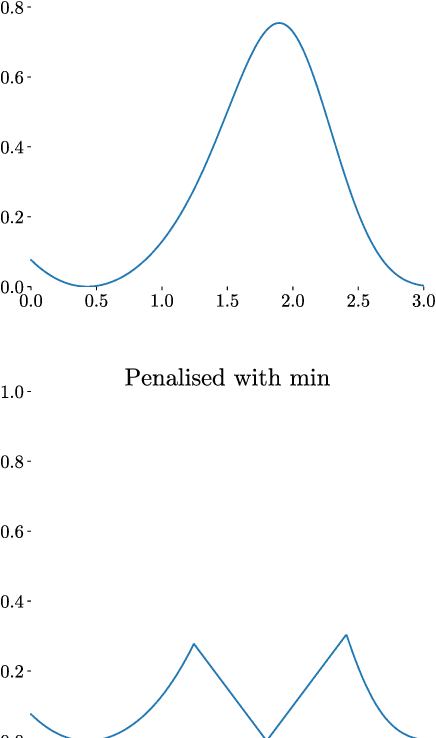
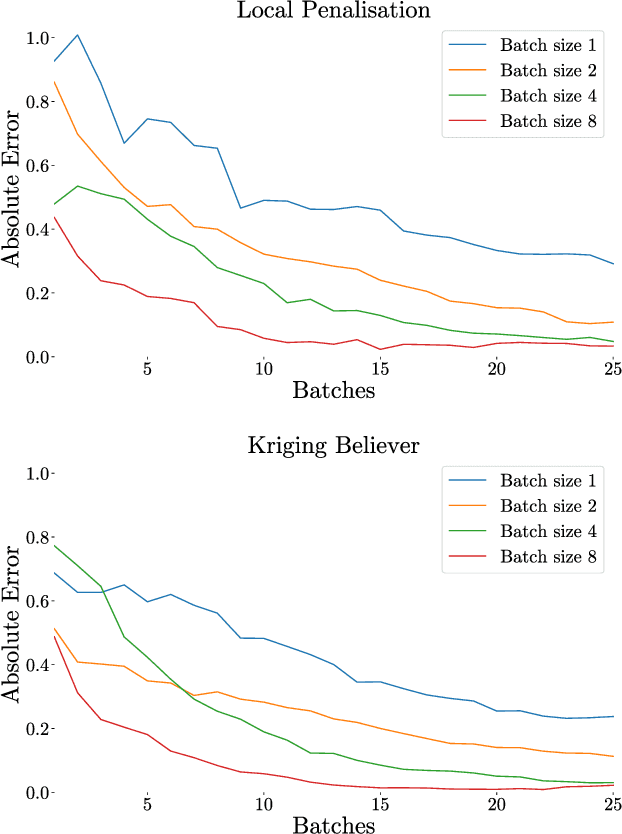
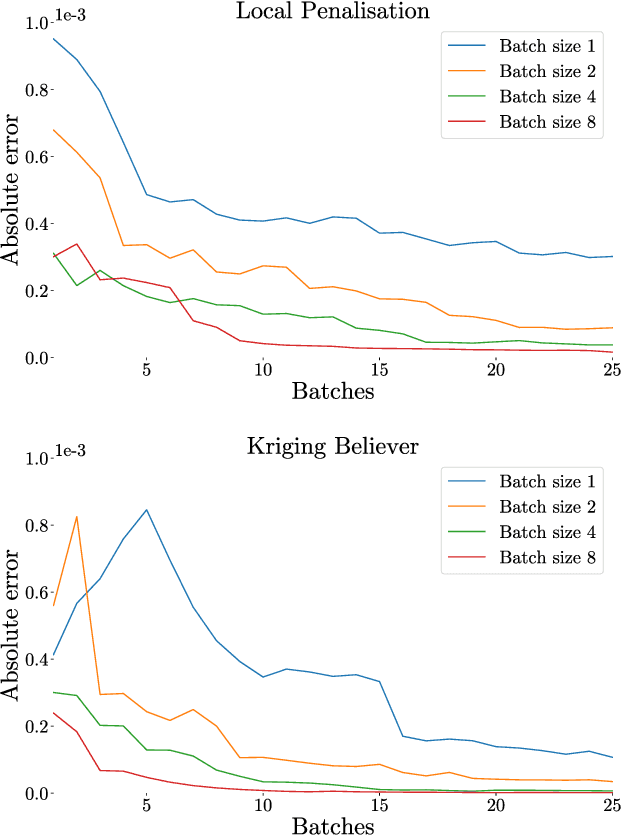
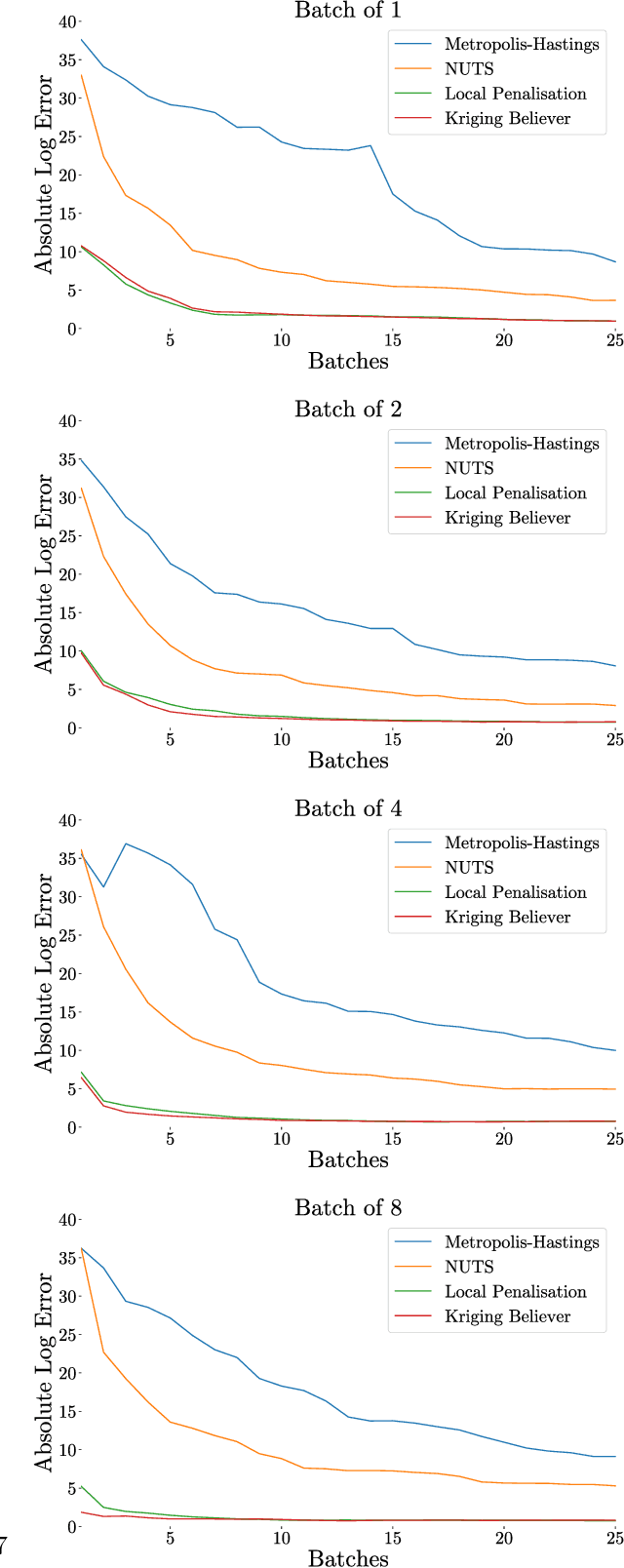
Integration over non-negative integrands is a central problem in machine learning (e.g. for model averaging, (hyper-)parameter marginalisation, and computing posterior predictive distributions). Bayesian Quadrature is a probabilistic numerical integration technique that performs promisingly when compared to traditional Markov Chain Monte Carlo methods. However, in contrast to easily-parallelised MCMC methods, Bayesian Quadrature methods have, thus far, been essentially serial in nature, selecting a single point to sample at each step of the algorithm. We deliver methods to select batches of points at each step, based upon those recently presented in the Batch Bayesian Optimisation literature. Such parallelisation significantly reduces computation time, especially when the integrand is expensive to sample.

Intersectionality: Multiple Group Fairness in Expectation Constraints

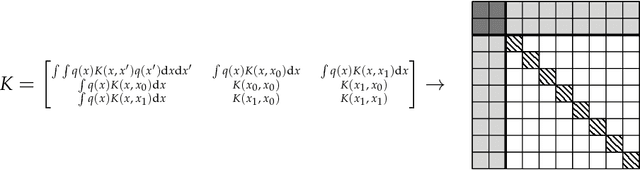
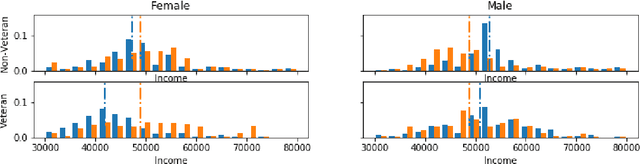
Group fairness is an important concern for machine learning researchers, developers, and regulators. However, the strictness to which models must be constrained to be considered fair is still under debate. The focus of this work is on constraining the expected outcome of subpopulations in kernel regression and, in particular, decision tree regression, with application to random forests, boosted trees and other ensemble models. While individual constraints were previously addressed, this work addresses concerns about incorporating multiple constraints simultaneously. The proposed solution does not affect the order of computational or memory complexity of the decision trees and is easily integrated into models post training.

Equality Constrained Decision Trees: For the Algorithmic Enforcement of Group Fairness

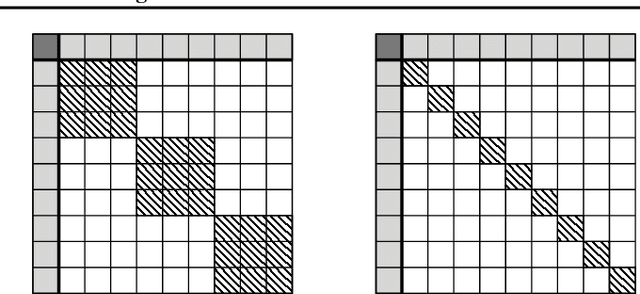
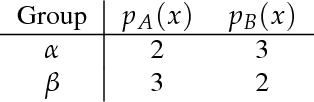
Fairness, through its many forms and definitions, has become an important issue facing the machine learning community. In this work, we consider how to incorporate group fairness constraints in kernel regression methods. More specifically, we focus on examining the incorporation of these constraints in decision tree regression when cast as a form of kernel regression, with direct applications to random forests and boosted trees amongst other widespread popular inference techniques. We show that order of complexity of memory and computation is preserved for such models and bounds the expected perturbations to the model in terms of the number of leaves of the trees. Importantly, the approach works on trained models and hence can be easily applied to models in current use.

Entropic Spectral Learning in Large Scale Networks

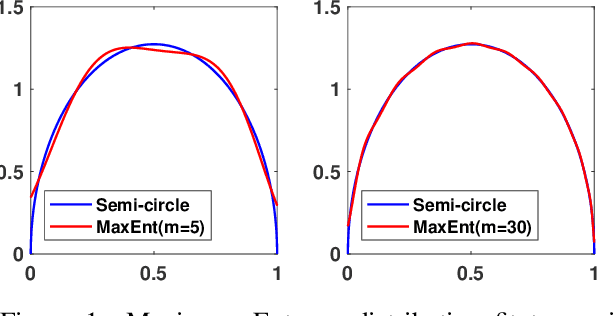
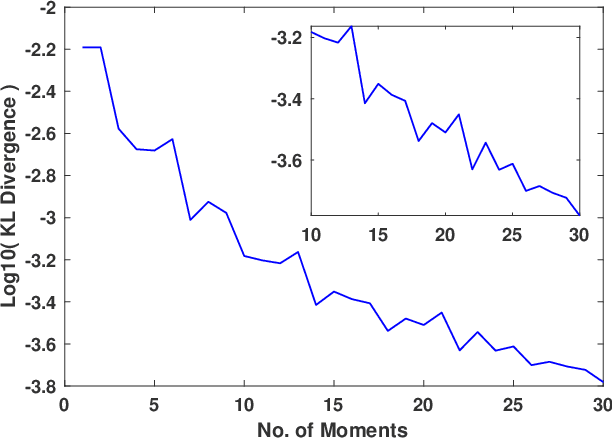
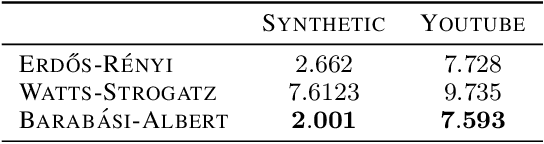
We present a novel algorithm for learning the spectral density of large scale networks using stochastic trace estimation and the method of maximum entropy. The complexity of the algorithm is linear in the number of non-zero elements of the matrix, offering a computational advantage over other algorithms. We apply our algorithm to the problem of community detection in large networks. We show state-of-the-art performance on both synthetic and real datasets.