Self-reflective Uncertainties: Do LLMs Know Their Internal Answer Distribution?

To reveal when a large language model (LLM) is uncertain about a response, uncertainty quantification commonly produces percentage numbers along with the output. But is this all we can do? We argue that in the output space of LLMs, the space of strings, exist strings expressive enough to summarize the distribution over output strings the LLM deems possible. We lay a foundation for this new avenue of uncertainty explication and present SelfReflect, a theoretically-motivated metric to assess how faithfully a string summarizes an LLM's internal answer distribution. We show that SelfReflect is able to discriminate even subtle differences of candidate summary strings and that it aligns with human judgement, outperforming alternative metrics such as LLM judges and embedding comparisons. With SelfReflect, we investigate a number of self-summarization methods and find that even state-of-the-art reasoning models struggle to explicate their internal uncertainty. But we find that faithful summarizations can be generated by sampling and summarizing. Our metric enables future works towards this universal form of LLM uncertainties.

Revisiting Uncertainty Quantification Evaluation in Language Models: Spurious Interactions with Response Length Bias Results

Uncertainty Quantification (UQ) in Language Models (LMs) is crucial for improving their safety and reliability. Evaluations often use performance metrics like AUROC to assess how well UQ methods (e.g., negative sequence probabilities) correlate with task correctness functions (e.g., ROUGE-L). In this paper, we show that commonly used correctness functions bias UQ evaluations by inflating the performance of certain UQ methods. We evaluate 7 correctness functions -- from lexical-based and embedding-based metrics to LLM-as-a-judge approaches -- across 4 datasets x 4 models x 6 UQ methods. Our analysis reveals that length biases in the errors of these correctness functions distort UQ assessments by interacting with length biases in UQ methods. We identify LLM-as-a-judge approaches as among the least length-biased choices and hence a potential solution to mitigate these biases.

Controlling Language and Diffusion Models by Transporting Activations

The increasing capabilities of large generative models and their ever more widespread deployment have raised concerns about their reliability, safety, and potential misuse. To address these issues, recent works have proposed to control model generation by steering model activations in order to effectively induce or prevent the emergence of concepts or behaviors in the generated output. In this paper we introduce Activation Transport (AcT), a general framework to steer activations guided by optimal transport theory that generalizes many previous activation-steering works. AcT is modality-agnostic and provides fine-grained control over the model behavior with negligible computational overhead, while minimally impacting model abilities. We experimentally show the effectiveness and versatility of our approach by addressing key challenges in large language models (LLMs) and text-to-image diffusion models (T2Is). For LLMs, we show that AcT can effectively mitigate toxicity, induce arbitrary concepts, and increase their truthfulness. In T2Is, we show how AcT enables fine-grained style control and concept negation.

Considerations for Distribution Shift Robustness of Diagnostic Models in Healthcare

We consider robustness to distribution shifts in the context of diagnostic models in healthcare, where the prediction target $Y$, e.g., the presence of a disease, is causally upstream of the observations $X$, e.g., a biomarker. Distribution shifts may occur, for instance, when the training data is collected in a domain with patients having particular demographic characteristics while the model is deployed on patients from a different demographic group. In the domain of applied ML for health, it is common to predict $Y$ from $X$ without considering further information about the patient. However, beyond the direct influence of the disease $Y$ on biomarker $X$, a predictive model may learn to exploit confounding dependencies (or shortcuts) between $X$ and $Y$ that are unstable under certain distribution shifts. In this work, we highlight a data generating mechanism common to healthcare settings and discuss how recent theoretical results from the causality literature can be applied to build robust predictive models. We theoretically show why ignoring covariates as well as common invariant learning approaches will in general not yield robust predictors in the studied setting, while including certain covariates into the prediction model will. In an extensive simulation study, we showcase the robustness (or lack thereof) of different predictors under various data generating processes. Lastly, we analyze the performance of the different approaches using the PTB-XL dataset, a public dataset of annotated ECG recordings.

Robust multimodal models have outlier features and encode more concepts

What distinguishes robust models from non-robust ones? This question has gained traction with the appearance of large-scale multimodal models, such as CLIP. These models have demonstrated unprecedented robustness with respect to natural distribution shifts. While it has been shown that such differences in robustness can be traced back to differences in training data, so far it is not known what that translates to in terms of what the model has learned. In this work, we bridge this gap by probing the representation spaces of 12 robust multimodal models with various backbones (ResNets and ViTs) and pretraining sets (OpenAI, LAION-400M, LAION-2B, YFCC15M, CC12M and DataComp). We find two signatures of robustness in the representation spaces of these models: (1) Robust models exhibit outlier features characterized by their activations, with some being several orders of magnitude above average. These outlier features induce privileged directions in the model's representation space. We demonstrate that these privileged directions explain most of the predictive power of the model by pruning up to $80 \%$ of the least important representation space directions without negative impacts on model accuracy and robustness; (2) Robust models encode substantially more concepts in their representation space. While this superposition of concepts allows robust models to store much information, it also results in highly polysemantic features, which makes their interpretation challenging. We discuss how these insights pave the way for future research in various fields, such as model pruning and mechanistic interpretability.

The Role of Entropy and Reconstruction in Multi-View Self-Supervised Learning

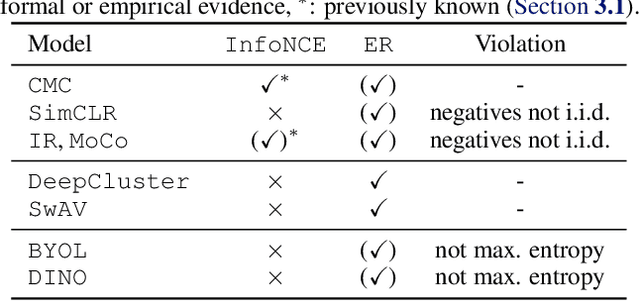
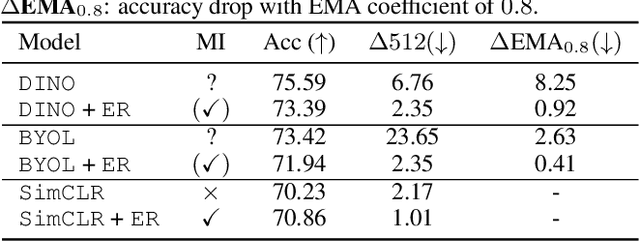
The mechanisms behind the success of multi-view self-supervised learning (MVSSL) are not yet fully understood. Contrastive MVSSL methods have been studied through the lens of InfoNCE, a lower bound of the Mutual Information (MI). However, the relation between other MVSSL methods and MI remains unclear. We consider a different lower bound on the MI consisting of an entropy and a reconstruction term (ER), and analyze the main MVSSL families through its lens. Through this ER bound, we show that clustering-based methods such as DeepCluster and SwAV maximize the MI. We also re-interpret the mechanisms of distillation-based approaches such as BYOL and DINO, showing that they explicitly maximize the reconstruction term and implicitly encourage a stable entropy, and we confirm this empirically. We show that replacing the objectives of common MVSSL methods with this ER bound achieves competitive performance, while making them stable when training with smaller batch sizes or smaller exponential moving average (EMA) coefficients. Github repo: https://github.com/apple/ml-entropy-reconstruction.

DUET: 2D Structured and Approximately Equivariant Representations

Multiview Self-Supervised Learning (MSSL) is based on learning invariances with respect to a set of input transformations. However, invariance partially or totally removes transformation-related information from the representations, which might harm performance for specific downstream tasks that require such information. We propose 2D strUctured and EquivarianT representations (coined DUET), which are 2d representations organized in a matrix structure, and equivariant with respect to transformations acting on the input data. DUET representations maintain information about an input transformation, while remaining semantically expressive. Compared to SimCLR (Chen et al., 2020) (unstructured and invariant) and ESSL (Dangovski et al., 2022) (unstructured and equivariant), the structured and equivariant nature of DUET representations enables controlled generation with lower reconstruction error, while controllability is not possible with SimCLR or ESSL. DUET also achieves higher accuracy for several discriminative tasks, and improves transfer learning.

Challenges of Adversarial Image Augmentations

Image augmentations applied during training are crucial for the generalization performance of image classifiers. Therefore, a large body of research has focused on finding the optimal augmentation policy for a given task. Yet, RandAugment [2], a simple random augmentation policy, has recently been shown to outperform existing sophisticated policies. Only Adversarial AutoAugment (AdvAA) [11], an approach based on the idea of adversarial training, has shown to be better than RandAugment. In this paper, we show that random augmentations are still competitive compared to an optimal adversarial approach, as well as to simple curricula, and conjecture that the success of AdvAA is due to the stochasticity of the policy controller network, which introduces a mild form of curriculum.

Adversarial Attacks on Graph Classification via Bayesian Optimisation

Graph neural networks, a popular class of models effective in a wide range of graph-based learning tasks, have been shown to be vulnerable to adversarial attacks. While the majority of the literature focuses on such vulnerability in node-level classification tasks, little effort has been dedicated to analysing adversarial attacks on graph-level classification, an important problem with numerous real-life applications such as biochemistry and social network analysis. The few existing methods often require unrealistic setups, such as access to internal information of the victim models, or an impractically-large number of queries. We present a novel Bayesian optimisation-based attack method for graph classification models. Our method is black-box, query-efficient and parsimonious with respect to the perturbation applied. We empirically validate the effectiveness and flexibility of the proposed method on a wide range of graph classification tasks involving varying graph properties, constraints and modes of attack. Finally, we analyse common interpretable patterns behind the adversarial samples produced, which may shed further light on the adversarial robustness of graph classification models.

On Invariance Penalties for Risk Minimization

The Invariant Risk Minimization (IRM) principle was first proposed by Arjovsky et al. [2019] to address the domain generalization problem by leveraging data heterogeneity from differing experimental conditions. Specifically, IRM seeks to find a data representation under which an optimal classifier remains invariant across all domains. Despite the conceptual appeal of IRM, the effectiveness of the originally proposed invariance penalty has recently been brought into question. In particular, there exists counterexamples for which that invariance penalty can be arbitrarily small for non-invariant data representations. We propose an alternative invariance penalty by revisiting the Gramian matrix of the data representation. We discuss the role of its eigenvalues in the relationship between the risk and the invariance penalty, and demonstrate that it is ill-conditioned for said counterexamples. The proposed approach is guaranteed to recover an invariant representation for linear settings under mild non-degeneracy conditions. Its effectiveness is substantiated by experiments on DomainBed and InvarianceUnitTest, two extensive test beds for domain generalization.