LaDDer: Latent Data Distribution Modelling with a Generative Prior

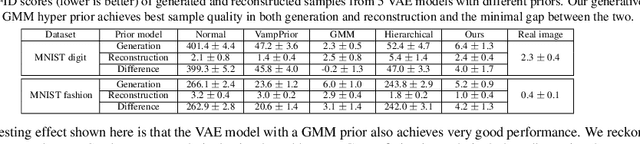
In this paper, we show that the performance of a learnt generative model is closely related to the model's ability to accurately represent the inferred \textbf{latent data distribution}, i.e. its topology and structural properties. We propose LaDDer to achieve accurate modelling of the latent data distribution in a variational autoencoder framework and to facilitate better representation learning. The central idea of LaDDer is a meta-embedding concept, which uses multiple VAE models to learn an embedding of the embeddings, forming a ladder of encodings. We use a non-parametric mixture as the hyper prior for the innermost VAE and learn all the parameters in a unified variational framework. From extensive experiments, we show that our LaDDer model is able to accurately estimate complex latent distribution and results in improvement in the representation quality. We also propose a novel latent space interpolation method that utilises the derived data distribution.

Balancing Reconstruction Quality and Regularisation in ELBO for VAEs

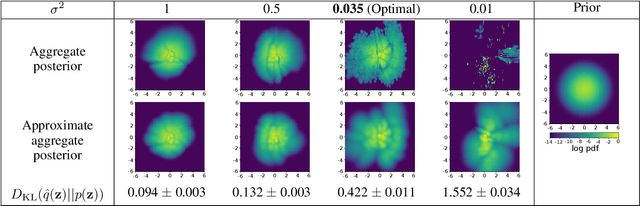
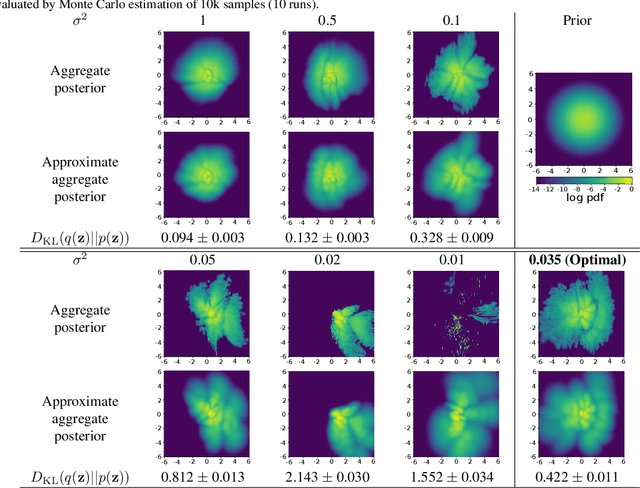
A trade-off exists between reconstruction quality and the prior regularisation in the Evidence Lower Bound (ELBO) loss that Variational Autoencoder (VAE) models use for learning. There are few satisfactory approaches to deal with a balance between the prior and reconstruction objective, with most methods dealing with this problem through heuristics. In this paper, we show that the noise variance (often set as a fixed value) in the Gaussian likelihood p(x|z) for real-valued data can naturally act to provide such a balance. By learning this noise variance so as to maximise the ELBO loss, we automatically obtain an optimal trade-off between the reconstruction error and the prior constraint on the posteriors. This variance can be interpreted intuitively as the necessary noise level for the current model to be the best explanation of the observed dataset. Further, by allowing the variance inference to be more flexible it can conveniently be used as an uncertainty estimator for reconstructed or generated samples. We demonstrate that optimising the noise variance is a crucial component of VAE learning, and showcase the performance on MNIST, Fashion MNIST and CelebA datasets. We find our approach can significantly improve the quality of generated samples whilst maintaining a smooth latent-space manifold to represent the data. The method also offers an indication of uncertainty in the final generative model.

WiSE-ALE: Wide Sample Estimator for Approximate Latent Embedding

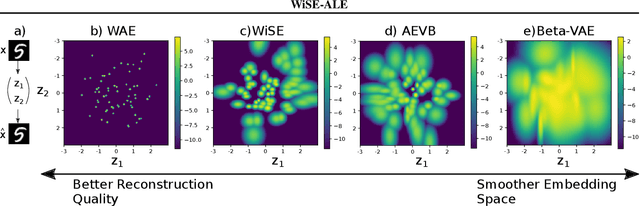
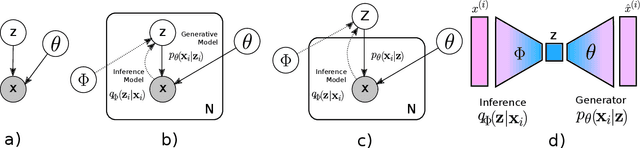
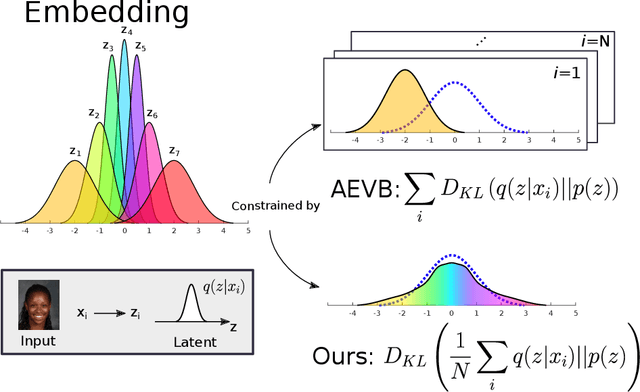
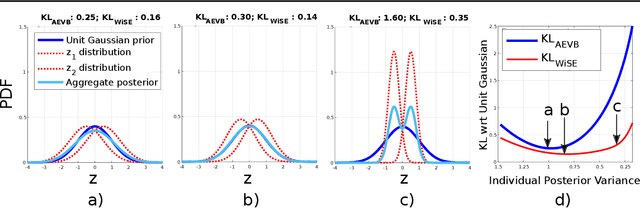
Variational Auto-encoders (VAEs) have been very successful as methods for forming compressed latent representations of complex, often high-dimensional, data. In this paper, we derive an alternative variational lower bound from the one common in VAEs, which aims to minimize aggregate information loss. Using our lower bound as the objective function for an auto-encoder enables us to place a prior on the bulk statistics, corresponding to an aggregate posterior for the entire dataset, as opposed to a single sample posterior as in the original VAE. This alternative form of prior constraint allows individual posteriors more flexibility to preserve necessary information for good reconstruction quality. We further derive an analytic approximation to our lower bound, leading to an efficient learning algorithm - WiSE-ALE. Through various examples, we demonstrate that WiSE-ALE can reach excellent reconstruction quality in comparison to other state-of-the-art VAE models, while still retaining the ability to learn a smooth, compact representation.