Operator Models for Continuous-Time Offline Reinforcement Learning

Continuous-time stochastic processes underlie many natural and engineered systems. In healthcare, autonomous driving, and industrial control, direct interaction with the environment is often unsafe or impractical, motivating offline reinforcement learning from historical data. However, there is limited statistical understanding of the approximation errors inherent in learning policies from offline datasets. We address this by linking reinforcement learning to the Hamilton-Jacobi-Bellman equation and proposing an operator-theoretic algorithm based on a simple dynamic programming recursion. Specifically, we represent our world model in terms of the infinitesimal generator of controlled diffusion processes learned in a reproducing kernel Hilbert space. By integrating statistical learning methods and operator theory, we establish global convergence of the value function and derive finite-sample guarantees with bounds tied to system properties such as smoothness and stability. Our theoretical and numerical results indicate that operator-based approaches may hold promise in solving offline reinforcement learning using continuous-time optimal control.

SAD-Flower: Flow Matching for Safe, Admissible, and Dynamically Consistent Planning

Flow matching (FM) has shown promising results in data-driven planning. However, it inherently lacks formal guarantees for ensuring state and action constraints, whose satisfaction is a fundamental and crucial requirement for the safety and admissibility of planned trajectories on various systems. Moreover, existing FM planners do not ensure the dynamical consistency, which potentially renders trajectories inexecutable. We address these shortcomings by proposing SAD-Flower, a novel framework for generating Safe, Admissible, and Dynamically consistent trajectories. Our approach relies on an augmentation of the flow with a virtual control input. Thereby, principled guidance can be derived using techniques from nonlinear control theory, providing formal guarantees for state constraints, action constraints, and dynamic consistency. Crucially, SAD-Flower operates without retraining, enabling test-time satisfaction of unseen constraints. Through extensive experiments across several tasks, we demonstrate that SAD-Flower outperforms various generative-model-based baselines in ensuring constraint satisfaction.

Koopman-Equivariant Gaussian Processes

Credible forecasting and representation learning of dynamical systems are of ever-increasing importance for reliable decision-making. To that end, we propose a family of Gaussian processes (GP) for dynamical systems with linear time-invariant responses, which are nonlinear only in initial conditions. This linearity allows us to tractably quantify forecasting and representational uncertainty, simultaneously alleviating the challenge of computing the distribution of trajectories from a GP-based dynamical system and enabling a new probabilistic treatment of learning Koopman operator representations. Using a trajectory-based equivariance -- which we refer to as \textit{Koopman equivariance} -- we obtain a GP model with enhanced generalization capabilities. To allow for large-scale regression, we equip our framework with variational inference based on suitable inducing points. Experiments demonstrate on-par and often better forecasting performance compared to kernel-based methods for learning dynamical systems.

Jacta: A Versatile Planner for Learning Dexterous and Whole-body Manipulation

Robotic manipulation is challenging due to discontinuous dynamics, as well as high-dimensional state and action spaces. Data-driven approaches that succeed in manipulation tasks require large amounts of data and expert demonstrations, typically from humans. Existing manipulation planners are restricted to specific systems and often depend on specialized algorithms for using demonstration. Therefore, we introduce a flexible motion planner tailored to dexterous and whole-body manipulation tasks. Our planner creates readily usable demonstrations for reinforcement learning algorithms, eliminating the need for additional training pipeline complexities. With this approach, we can efficiently learn policies for complex manipulation tasks, where traditional reinforcement learning alone only makes little progress. Furthermore, we demonstrate that learned policies are transferable to real robotic systems for solving complex dexterous manipulation tasks.

Data-Driven Optimal Feedback Laws via Kernel Mean Embeddings

This paper proposes a fully data-driven approach for optimal control of nonlinear control-affine systems represented by a stochastic diffusion. The focus is on the scenario where both the nonlinear dynamics and stage cost functions are unknown, while only control penalty function and constraints are provided. Leveraging the theory of reproducing kernel Hilbert spaces, we introduce novel kernel mean embeddings (KMEs) to identify the Markov transition operators associated with controlled diffusion processes. The KME learning approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions. Thus, unlike traditional dynamic programming methods, our approach exploits the ``kernel trick'' to break the curse of dimensionality. We demonstrate the effectiveness of our method through numerical examples, highlighting its ability to solve a large class of nonlinear optimal control problems.

Nonparametric Control-Koopman Operator Learning: Flexible and Scalable Models for Prediction and Control

Linearity of Koopman operators and simplicity of their estimators coupled with model-reduction capabilities has lead to their great popularity in applications for learning dynamical systems. While nonparametric Koopman operator learning in infinite-dimensional reproducing kernel Hilbert spaces is well understood for autonomous systems, its control system analogues are largely unexplored. Addressing systems with control inputs in a principled manner is crucial for fully data-driven learning of controllers, especially since existing approaches commonly resort to representational heuristics or parametric models of limited expressiveness and scalability. We address the aforementioned challenge by proposing a universal framework via control-affine reproducing kernels that enables direct estimation of a single operator even for control systems. The proposed approach, called control-Koopman operator regression (cKOR), is thus completely analogous to Koopman operator regression of the autonomous case. First in the literature, we present a nonparametric framework for learning Koopman operator representations of nonlinear control-affine systems that does not suffer from the curse of control input dimensionality. This allows for reformulating the infinite-dimensional learning problem in a finite-dimensional space based solely on data without apriori loss of precision due to a restriction to a finite span of functions or inputs as in other approaches. For enabling applications to large-scale control systems, we also enhance the scalability of control-Koopman operator estimators by leveraging random projections (sketching). The efficacy of our novel cKOR approach is demonstrated on both forecasting and control tasks.

Cooperative Learning with Gaussian Processes for Euler-Lagrange Systems Tracking Control under Switching Topologies

This work presents an innovative learning-based approach to tackle the tracking control problem of Euler-Lagrange multi-agent systems with partially unknown dynamics operating under switching communication topologies. The approach leverages a correlation-aware cooperative algorithm framework built upon Gaussian process regression, which adeptly captures inter-agent correlations for uncertainty predictions. A standout feature is its exceptional efficiency in deriving the aggregation weights achieved by circumventing the computationally intensive posterior variance calculations. Through Lyapunov stability analysis, the distributed control law ensures bounded tracking errors with high probability. Simulation experiments validate the protocol's efficacy in effectively managing complex scenarios, establishing it as a promising solution for robust tracking control in multi-agent systems characterized by uncertain dynamics and dynamic communication structures.

Koopman Kernel Regression

Many machine learning approaches for decision making, such as reinforcement learning, rely on simulators or predictive models to forecast the time-evolution of quantities of interest, e.g., the state of an agent or the reward of a policy. Forecasts of such complex phenomena are commonly described by highly nonlinear dynamical systems, making their use in optimization-based decision-making challenging. Koopman operator theory offers a beneficial paradigm for addressing this problem by characterizing forecasts via linear dynamical systems. This makes system analysis and long-term predictions simple -- involving only matrix multiplications. However, the transformation to a linear system is generally non-trivial and unknown, requiring learning-based approaches. While there exists a variety of approaches, they usually lack crucial learning-theoretic guarantees, such that the behavior of the obtained models with increasing data and dimensionality is often unclear. We address the aforementioned by deriving a novel reproducing kernel Hilbert space (RKHS) that solely spans transformations into linear dynamical systems. The resulting Koopman Kernel Regression (KKR) framework enables the use of statistical learning tools from function approximation for novel convergence results and generalization risk bounds under weaker assumptions than existing work. Our numerical experiments indicate advantages over state-of-the-art statistical learning approaches for Koopman-based predictors.

Variational Integrators and Graph-Based Solvers for Multibody Dynamics in Maximal Coordinates

Multibody dynamics simulators are an important tool in many fields, including learning and control for robotics. However, many existing dynamics simulators suffer from inaccuracies when dealing with constrained mechanical systems due to unsuitable integrators and dissatisfying constraint handling. Variational integrators are numerical discretization methods that can reduce physical inaccuracies when simulating mechanical systems, and formulating the dynamics in maximal coordinates allows for easy and numerically robust incorporation of constraints such as kinematic loops or contacts. Therefore, this article derives a variational integrator for mechanical systems with equality and inequality constraints in maximal coordinates. Additionally, efficient graph-based sparsity-exploiting algorithms for solving the integrator are provided and implemented as an open-source simulator. The evaluation of the simulator shows the improved physical accuracy due to the variational integrator and the advantages of the sparse solvers, while application examples of a walking robot and an exoskeleton with explicit constraints demonstrate the necessity and capabilities of maximal coordinates.

Dext-Gen: Dexterous Grasping in Sparse Reward Environments with Full Orientation Control

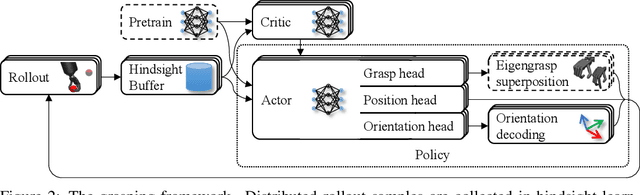
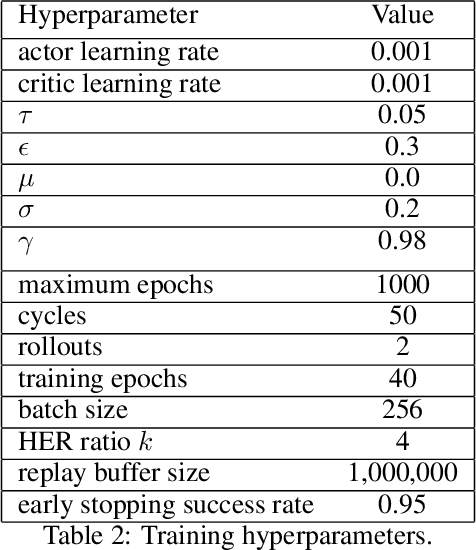
Reinforcement learning is a promising method for robotic grasping as it can learn effective reaching and grasping policies in difficult scenarios. However, achieving human-like manipulation capabilities with sophisticated robotic hands is challenging because of the problem's high dimensionality. Although remedies such as reward shaping or expert demonstrations can be employed to overcome this issue, they often lead to oversimplified and biased policies. We present Dext-Gen, a reinforcement learning framework for Dexterous Grasping in sparse reward ENvironments that is applicable to a variety of grippers and learns unbiased and intricate policies. Full orientation control of the gripper and object is achieved through smooth orientation representation. Our approach has reasonable training durations and provides the option to include desired prior knowledge. The effectiveness and adaptability of the framework to different scenarios is demonstrated in simulated experiments.