Are LLM Decisions Faithful to Verbal Confidence?

Large Language Models (LLMs) can produce surprisingly sophisticated estimates of their own uncertainty. However, it remains unclear to what extent this expressed confidence is tied to the reasoning, knowledge, or decision making of the model. To test this, we introduce $\textbf{RiskEval}$: a framework designed to evaluate whether models adjust their abstention policies in response to varying error penalties. Our evaluation of several frontier models reveals a critical dissociation: models are neither cost-aware when articulating their verbal confidence, nor strategically responsive when deciding whether to engage or abstain under high-penalty conditions. Even when extreme penalties render frequent abstention the mathematically optimal strategy, models almost never abstain, resulting in utility collapse. This indicates that calibrated verbal confidence scores may not be sufficient to create trustworthy and interpretable AI systems, as current models lack the strategic agency to convert uncertainty signals into optimal and risk-sensitive decisions.

From Calibration to Collaboration: LLM Uncertainty Quantification Should Be More Human-Centered

Large Language Models (LLMs) are increasingly assisting users in the real world, yet their reliability remains a concern. Uncertainty quantification (UQ) has been heralded as a tool to enhance human-LLM collaboration by enabling users to know when to trust LLM predictions. We argue that current practices for uncertainty quantification in LLMs are not optimal for developing useful UQ for human users making decisions in real-world tasks. Through an analysis of 40 LLM UQ methods, we identify three prevalent practices hindering the community's progress toward its goal of benefiting downstream users: 1) evaluating on benchmarks with low ecological validity; 2) considering only epistemic uncertainty; and 3) optimizing metrics that are not necessarily indicative of downstream utility. For each issue, we propose concrete user-centric practices and research directions that LLM UQ researchers should consider. Instead of hill-climbing on unrepresentative tasks using imperfect metrics, we argue that the community should adopt a more human-centered approach to LLM uncertainty quantification.

An Efficient Plugin Method for Metric Optimization of Black-Box Models

Many machine learning algorithms and classifiers are available only via API queries as a ``black-box'' -- that is, the downstream user has no ability to change, re-train, or fine-tune the model on a particular target distribution. Indeed, the downstream user may not even have knowledge of the \emph{original} training distribution or performance metric used to construct and optimize the black-box model. We propose a simple and efficient method, Plugin, which \emph{post-processes} arbitrary multiclass predictions from any black-box classifier in order to simultaneously (1) adapt these predictions to a target distribution; and (2) optimize a particular metric of the confusion matrix. Importantly, Plugin is a completely \textit{post-hoc} method which does not rely on feature information, only requires a small amount of probabilistic predictions along with their corresponding true label, and optimizes metrics by querying. We empirically demonstrate that Plugin is both broadly applicable and has performance competitive with related methods on a variety of tabular and language tasks.

When is Multicalibration Post-Processing Necessary?

Calibration is a well-studied property of predictors which guarantees meaningful uncertainty estimates. Multicalibration is a related notion -- originating in algorithmic fairness -- which requires predictors to be simultaneously calibrated over a potentially complex and overlapping collection of protected subpopulations (such as groups defined by ethnicity, race, or income). We conduct the first comprehensive study evaluating the usefulness of multicalibration post-processing across a broad set of tabular, image, and language datasets for models spanning from simple decision trees to 90 million parameter fine-tuned LLMs. Our findings can be summarized as follows: (1) models which are calibrated out of the box tend to be relatively multicalibrated without any additional post-processing; (2) multicalibration post-processing can help inherently uncalibrated models; and (3) traditional calibration measures may sometimes provide multicalibration implicitly. More generally, we also distill many independent observations which may be useful for practical and effective applications of multicalibration post-processing in real-world contexts.

Learnability is a Compact Property

Recent work on learning has yielded a striking result: the learnability of various problems can be undecidable, or independent of the standard ZFC axioms of set theory. Furthermore, the learnability of such problems can fail to be a property of finite character: informally, it cannot be detected by examining finite projections of the problem. On the other hand, learning theory abounds with notions of dimension that characterize learning and consider only finite restrictions of the problem, i.e., are properties of finite character. How can these results be reconciled? More precisely, which classes of learning problems are vulnerable to logical undecidability, and which are within the grasp of finite characterizations? We demonstrate that the difficulty of supervised learning with metric losses admits a tight finite characterization. In particular, we prove that the sample complexity of learning a hypothesis class can be detected by examining its finite projections. For realizable and agnostic learning with respect to a wide class of proper loss functions, we demonstrate an exact compactness result: a class is learnable with a given sample complexity precisely when the same is true of all its finite projections. For realizable learning with improper loss functions, we show that exact compactness of sample complexity can fail, and provide matching upper and lower bounds of a factor of 2 on the extent to which such sample complexities can differ. We conjecture that larger gaps are possible for the agnostic case. At the heart of our technical work is a compactness result concerning assignments of variables that maintain a class of functions below a target value, which generalizes Hall's classic matching theorem and may be of independent interest.

Stability and Multigroup Fairness in Ranking with Uncertain Predictions

Rankings are ubiquitous across many applications, from search engines to hiring committees. In practice, many rankings are derived from the output of predictors. However, when predictors trained for classification tasks have intrinsic uncertainty, it is not obvious how this uncertainty should be represented in the derived rankings. Our work considers ranking functions: maps from individual predictions for a classification task to distributions over rankings. We focus on two aspects of ranking functions: stability to perturbations in predictions and fairness towards both individuals and subgroups. Not only is stability an important requirement for its own sake, but -- as we show -- it composes harmoniously with individual fairness in the sense of Dwork et al. (2012). While deterministic ranking functions cannot be stable aside from trivial scenarios, we show that the recently proposed uncertainty aware (UA) ranking functions of Singh et al. (2021) are stable. Our main result is that UA rankings also achieve multigroup fairness through successful composition with multiaccurate or multicalibrated predictors. Our work demonstrates that UA rankings naturally interpolate between group and individual level fairness guarantees, while simultaneously satisfying stability guarantees important whenever machine-learned predictions are used.

Regularization and Optimal Multiclass Learning

The quintessential learning algorithm of empirical risk minimization (ERM) is known to fail in various settings for which uniform convergence does not characterize learning. It is therefore unsurprising that the practice of machine learning is rife with considerably richer algorithmic techniques for successfully controlling model capacity. Nevertheless, no such technique or principle has broken away from the pack to characterize optimal learning in these more general settings. The purpose of this work is to characterize the role of regularization in perhaps the simplest setting for which ERM fails: multiclass learning with arbitrary label sets. Using one-inclusion graphs (OIGs), we exhibit optimal learning algorithms that dovetail with tried-and-true algorithmic principles: Occam's Razor as embodied by structural risk minimization (SRM), the principle of maximum entropy, and Bayesian reasoning. Most notably, we introduce an optimal learner which relaxes structural risk minimization on two dimensions: it allows the regularization function to be "local" to datapoints, and uses an unsupervised learning stage to learn this regularizer at the outset. We justify these relaxations by showing that they are necessary: removing either dimension fails to yield a near-optimal learner. We also extract from OIGs a combinatorial sequence we term the Hall complexity, which is the first to characterize a problem's transductive error rate exactly. Lastly, we introduce a generalization of OIGs and the transductive learning setting to the agnostic case, where we show that optimal orientations of Hamming graphs -- judged using nodes' outdegrees minus a system of node-dependent credits -- characterize optimal learners exactly. We demonstrate that an agnostic version of the Hall complexity again characterizes error rates exactly, and exhibit an optimal learner using maximum entropy programs.

Fairness in Matching under Uncertainty

The prevalence and importance of algorithmic two-sided marketplaces has drawn attention to the issue of fairness in such settings. Algorithmic decisions are used in assigning students to schools, users to advertisers, and applicants to job interviews. These decisions should heed the preferences of individuals, and simultaneously be fair with respect to their merits (synonymous with fit, future performance, or need). Merits conditioned on observable features are always uncertain, a fact that is exacerbated by the widespread use of machine learning algorithms to infer merit from the observables. As our key contribution, we carefully axiomatize a notion of individual fairness in the two-sided marketplace setting which respects the uncertainty in the merits; indeed, it simultaneously recognizes uncertainty as the primary potential cause of unfairness and an approach to address it. We design a linear programming framework to find fair utility-maximizing distributions over allocations, and we show that the linear program is robust to perturbations in the estimated parameters of the uncertain merit distributions, a key property in combining the approach with machine learning techniques.

Polynomial Time Reinforcement Learning in Correlated FMDPs with Linear Value Functions

Many reinforcement learning (RL) environments in practice feature enormous state spaces that may be described compactly by a "factored" structure, that may be modeled by Factored Markov Decision Processes (FMDPs). We present the first polynomial-time algorithm for RL with FMDPs that does not rely on an oracle planner, and instead of requiring a linear transition model, only requires a linear value function with a suitable local basis with respect to the factorization. With this assumption, we can solve FMDPs in polynomial time by constructing an efficient separation oracle for convex optimization. Importantly, and in contrast to prior work, we do not assume that the transitions on various factors are independent.

Failout: Achieving Failure-Resilient Inference in Distributed Neural Networks

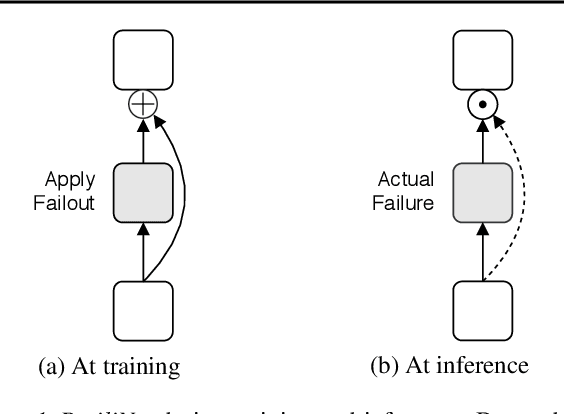
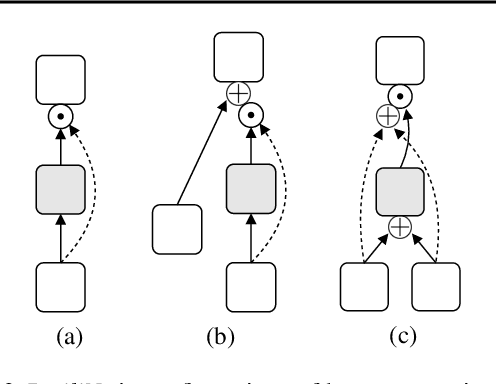
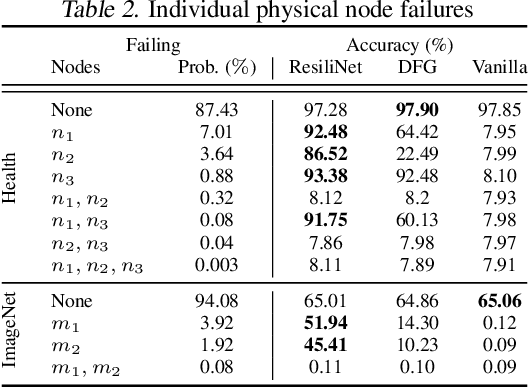
When a neural network is partitioned and distributed across physical nodes, failure of physical nodes causes the failure of the neural units that are placed on those nodes, which results in a significant performance drop. Current approaches focus on resiliency of training in distributed neural networks. However, resiliency of inference in distributed neural networks is less explored. We introduce ResiliNet, a scheme for making inference in distributed neural networks resilient to physical node failures. ResiliNet combines two concepts to provide resiliency: skip connection in residual neural networks, and a novel technique called failout, which is introduced in this paper. Failout simulates physical node failure conditions during training using dropout, and is specifically designed to improve the resiliency of distributed neural networks. The results of the experiments and ablation studies using three datasets confirm the ability of ResiliNet to provide inference resiliency for distributed neural networks.