Is Transductive Learning Equivalent to PAC Learning?

Most work in the area of learning theory has focused on designing effective Probably Approximately Correct (PAC) learners. Recently, other models of learning such as transductive error have seen more scrutiny. We move toward showing that these problems are equivalent by reducing agnostic learning with a PAC guarantee to agnostic learning with a transductive guarantee by adding a small number of samples to the dataset. We first rederive the result of Aden-Ali et al. arXiv:2304.09167 reducing PAC learning to transductive learning in the realizable setting using simpler techniques and at more generality as background for our main positive result. Our agnostic transductive to PAC conversion technique extends the aforementioned argument to the agnostic case, showing that an agnostic transductive learner can be efficiently converted to an agnostic PAC learner. Finally, we characterize the performance of the agnostic one inclusion graph algorithm of Asilis et al. arXiv:2309.13692 for binary classification, and show that plugging it into our reduction leads to an agnostic PAC learner that is essentially optimal. Our results imply that transductive and PAC learning are essentially equivalent for supervised learning with pseudometric losses in the realizable setting, and for binary classification in the agnostic setting. We conjecture this is true more generally for the agnostic setting.

Learnability is a Compact Property

Recent work on learning has yielded a striking result: the learnability of various problems can be undecidable, or independent of the standard ZFC axioms of set theory. Furthermore, the learnability of such problems can fail to be a property of finite character: informally, it cannot be detected by examining finite projections of the problem. On the other hand, learning theory abounds with notions of dimension that characterize learning and consider only finite restrictions of the problem, i.e., are properties of finite character. How can these results be reconciled? More precisely, which classes of learning problems are vulnerable to logical undecidability, and which are within the grasp of finite characterizations? We demonstrate that the difficulty of supervised learning with metric losses admits a tight finite characterization. In particular, we prove that the sample complexity of learning a hypothesis class can be detected by examining its finite projections. For realizable and agnostic learning with respect to a wide class of proper loss functions, we demonstrate an exact compactness result: a class is learnable with a given sample complexity precisely when the same is true of all its finite projections. For realizable learning with improper loss functions, we show that exact compactness of sample complexity can fail, and provide matching upper and lower bounds of a factor of 2 on the extent to which such sample complexities can differ. We conjecture that larger gaps are possible for the agnostic case. At the heart of our technical work is a compactness result concerning assignments of variables that maintain a class of functions below a target value, which generalizes Hall's classic matching theorem and may be of independent interest.

Regularization and Optimal Multiclass Learning

The quintessential learning algorithm of empirical risk minimization (ERM) is known to fail in various settings for which uniform convergence does not characterize learning. It is therefore unsurprising that the practice of machine learning is rife with considerably richer algorithmic techniques for successfully controlling model capacity. Nevertheless, no such technique or principle has broken away from the pack to characterize optimal learning in these more general settings. The purpose of this work is to characterize the role of regularization in perhaps the simplest setting for which ERM fails: multiclass learning with arbitrary label sets. Using one-inclusion graphs (OIGs), we exhibit optimal learning algorithms that dovetail with tried-and-true algorithmic principles: Occam's Razor as embodied by structural risk minimization (SRM), the principle of maximum entropy, and Bayesian reasoning. Most notably, we introduce an optimal learner which relaxes structural risk minimization on two dimensions: it allows the regularization function to be "local" to datapoints, and uses an unsupervised learning stage to learn this regularizer at the outset. We justify these relaxations by showing that they are necessary: removing either dimension fails to yield a near-optimal learner. We also extract from OIGs a combinatorial sequence we term the Hall complexity, which is the first to characterize a problem's transductive error rate exactly. Lastly, we introduce a generalization of OIGs and the transductive learning setting to the agnostic case, where we show that optimal orientations of Hamming graphs -- judged using nodes' outdegrees minus a system of node-dependent credits -- characterize optimal learners exactly. We demonstrate that an agnostic version of the Hall complexity again characterizes error rates exactly, and exhibit an optimal learner using maximum entropy programs.

Mitigating the Curse of Correlation in Security Games by Entropy Maximization

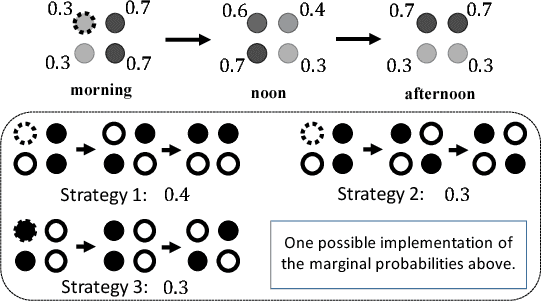
In Stackelberg security games, a defender seeks to randomly allocate limited security resources to protect critical targets from an attack. In this paper, we study a fundamental, yet underexplored, phenomenon in security games, which we term the \emph{Curse of Correlation} (CoC). Specifically, we observe that there are inevitable correlations among the protection status of different targets. Such correlation is a crucial concern, especially in \emph{spatio-temporal} domains like conservation area patrolling, where attackers can surveil patrollers at certain areas and then infer their patrolling routes using such correlations. To mitigate this issue, we propose to design entropy-maximizing defending strategies for spatio-temporal security games, which frequently suffer from CoC. We prove that the problem is \#P-hard in general. However, it admits efficient algorithms in well-motivated special settings. Our experiments show significant advantages of max-entropy algorithms over previous algorithms. A scalable implementation of our algorithm is currently under pre-deployment testing for integration into FAMS software to improve the scheduling of US federal air marshals.

On the Distortion of Voting with Multiple Representative Candidates

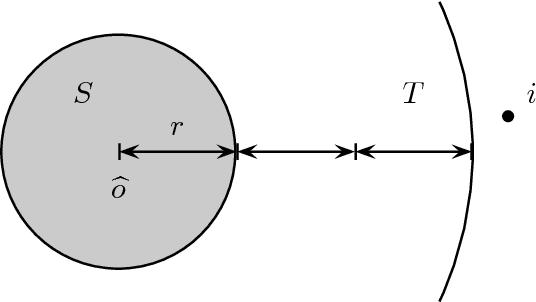
We study positional voting rules when candidates and voters are embedded in a common metric space, and cardinal preferences are naturally given by distances in the metric space. In a positional voting rule, each candidate receives a score from each ballot based on the ballot's rank order; the candidate with the highest total score wins the election. The cost of a candidate is his sum of distances to all voters, and the distortion of an election is the ratio between the cost of the elected candidate and the cost of the optimum candidate. We consider the case when candidates are representative of the population, in the sense that they are drawn i.i.d. from the population of the voters, and analyze the expected distortion of positional voting rules. Our main result is a clean and tight characterization of positional voting rules that have constant expected distortion (independent of the number of candidates and the metric space). Our characterization result immediately implies constant expected distortion for Borda Count and elections in which each voter approves a constant fraction of all candidates. On the other hand, we obtain super-constant expected distortion for Plurality, Veto, and approving a constant number of candidates. These results contrast with previous results on voting with metric preferences: When the candidates are chosen adversarially, all of the preceding voting rules have distortion linear in the number of candidates or voters. Thus, the model of representative candidates allows us to distinguish voting rules which seem equally bad in the worst case.

Of the People: Voting Is More Effective with Representative Candidates

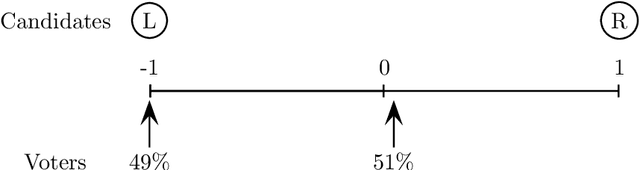
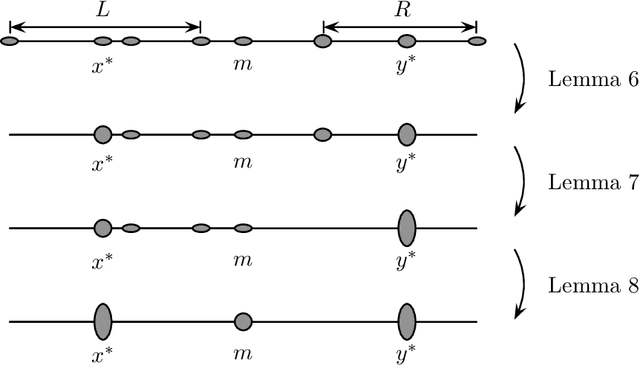
In light of the classic impossibility results of Arrow and Gibbard and Satterthwaite regarding voting with ordinal rules, there has been recent interest in characterizing how well common voting rules approximate the social optimum. In order to quantify the quality of approximation, it is natural to consider the candidates and voters as embedded within a common metric space, and to ask how much further the chosen candidate is from the population as compared to the socially optimal one. We use this metric preference model to explore a fundamental and timely question: does the social welfare of a population improve when candidates are representative of the population? If so, then by how much, and how does the answer depend on the complexity of the metric space? We restrict attention to the most fundamental and common social choice setting: a population of voters, two independently drawn candidates, and a majority rule election. When candidates are not representative of the population, it is known that the candidate selected by the majority rule can be thrice as far from the population as the socially optimal one. We examine how this ratio improves when candidates are drawn independently from the population of voters. Our results are two-fold: When the metric is a line, the ratio improves from $3$ to $4-2\sqrt{2}$, roughly $1.1716$; this bound is tight. When the metric is arbitrary, we show a lower bound of $1.5$ and a constant upper bound strictly better than $2$ on the approximation ratio of the majority rule. The positive result depends in part on the assumption that candidates are independent and identically distributed. However, we show that independence alone is not enough to achieve the upper bound: even when candidates are drawn independently, if the population of candidates can be different from the voters, then an upper bound of $2$ on the approximation is tight.

Security Games with Information Leakage: Modeling and Computation

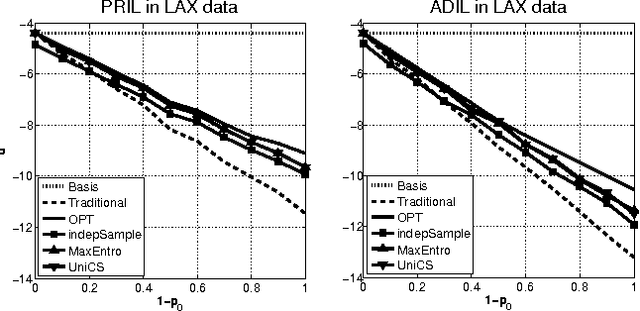
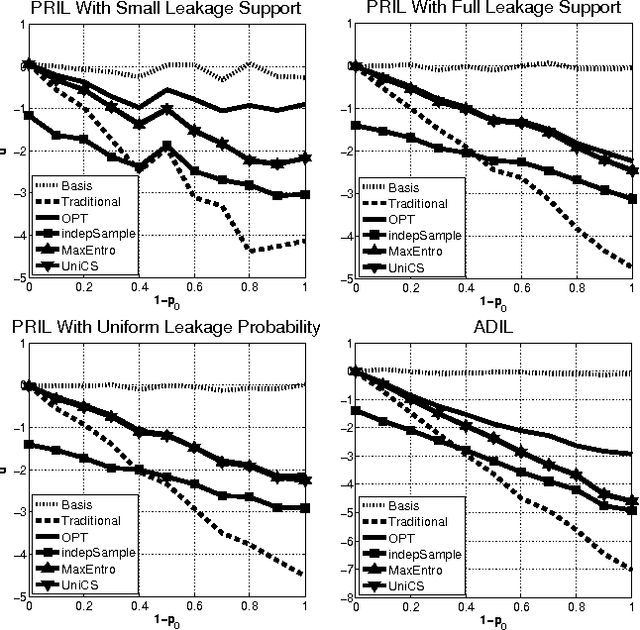
Most models of Stackelberg security games assume that the attacker only knows the defender's mixed strategy, but is not able to observe (even partially) the instantiated pure strategy. Such partial observation of the deployed pure strategy -- an issue we refer to as information leakage -- is a significant concern in practical applications. While previous research on patrolling games has considered the attacker's real-time surveillance, our settings, therefore models and techniques, are fundamentally different. More specifically, after describing the information leakage model, we start with an LP formulation to compute the defender's optimal strategy in the presence of leakage. Perhaps surprisingly, we show that a key subproblem to solve this LP (more precisely, the defender oracle) is NP-hard even for the simplest of security game models. We then approach the problem from three possible directions: efficient algorithms for restricted cases, approximation algorithms, and heuristic algorithms for sampling that improves upon the status quo. Our experiments confirm the necessity of handling information leakage and the advantage of our algorithms.

Dynamic Pricing with Limited Supply

We consider the problem of dynamic pricing with limited supply. A seller has $k$ identical items for sale and is facing $n$ potential buyers ("agents") that are arriving sequentially. Each agent is interested in buying one item. Each agent's value for an item is an IID sample from some fixed distribution with support $[0,1]$. The seller offers a take-it-or-leave-it price to each arriving agent (possibly different for different agents), and aims to maximize his expected revenue. We focus on "prior-independent" mechanisms -- ones that do not use any information about the distribution. They are desirable because knowing the distribution is unrealistic in many practical scenarios. We study how the revenue of such mechanisms compares to the revenue of the optimal offline mechanism that knows the distribution ("offline benchmark"). We present a prior-independent dynamic pricing mechanism whose revenue is at most $O((k \log n)^{2/3})$ less than the offline benchmark, for every distribution that is regular. In fact, this guarantee holds without *any* assumptions if the benchmark is relaxed to fixed-price mechanisms. Further, we prove a matching lower bound. The performance guarantee for the same mechanism can be improved to $O(\sqrt{k} \log n)$, with a distribution-dependent constant, if $k/n$ is sufficiently small. We show that, in the worst case over all demand distributions, this is essentially the best rate that can be obtained with a distribution-specific constant. On a technical level, we exploit the connection to multi-armed bandits (MAB). While dynamic pricing with unlimited supply can easily be seen as an MAB problem, the intuition behind MAB approaches breaks when applied to the setting with limited supply. Our high-level conceptual contribution is that even the limited supply setting can be fruitfully treated as a bandit problem.