Full Proportional Justified Representation

In multiwinner approval voting, forming a committee that proportionally represents voters' approval ballots is an essential task. The notion of justified representation (JR) demands that any large "cohesive" group of voters should be proportionally "represented". The "cohesiveness" is defined in different ways; two common ways are the following: (C1) demands that the group unanimously approves a set of candidates proportional to its size, while (C2) requires each member to approve at least a fixed fraction of such a set. Similarly, "representation" have been considered in different ways: (R1) the coalition's collective utility from the winning set exceeds that of any proportionally sized alternative, and (R2) for any proportionally sized alternative, at least one member of the coalition derives less utility from it than from the winning set. Three of the four possible combinations have been extensively studied: (C1)-(R1) defines Proportional Justified Representation (PJR), (C1)-(R2) defines Extended Justified Representation (EJR), (C2)-(R2) defines Full Justified Representation (FJR). All three have merits, but also drawbacks. PJR is the weakest notion, and perhaps not sufficiently demanding; EJR may not be compatible with perfect representation; and it is open whether a committee satisfying FJR can be found efficiently. We study the combination (C2)-(R1), which we call Full Proportional Justified Representation (FPJR). We investigate FPJR's properties and find that it shares PJR's advantages over EJR: several proportionality axioms (e.g. priceability, perfect representation) imply FPJR and PJR but not EJR. We also find that efficient rules like the greedy Monroe rule and the method of equal shares satisfy FPJR, matching a key advantage of EJR over FJR. However, the Proportional Approval Voting (PAV) rule may violate FPJR, so neither of EJR and FPJR implies the other.

Stability and Multigroup Fairness in Ranking with Uncertain Predictions

Rankings are ubiquitous across many applications, from search engines to hiring committees. In practice, many rankings are derived from the output of predictors. However, when predictors trained for classification tasks have intrinsic uncertainty, it is not obvious how this uncertainty should be represented in the derived rankings. Our work considers ranking functions: maps from individual predictions for a classification task to distributions over rankings. We focus on two aspects of ranking functions: stability to perturbations in predictions and fairness towards both individuals and subgroups. Not only is stability an important requirement for its own sake, but -- as we show -- it composes harmoniously with individual fairness in the sense of Dwork et al. (2012). While deterministic ranking functions cannot be stable aside from trivial scenarios, we show that the recently proposed uncertainty aware (UA) ranking functions of Singh et al. (2021) are stable. Our main result is that UA rankings also achieve multigroup fairness through successful composition with multiaccurate or multicalibrated predictors. Our work demonstrates that UA rankings naturally interpolate between group and individual level fairness guarantees, while simultaneously satisfying stability guarantees important whenever machine-learned predictions are used.

Proportional Representation in Metric Spaces and Low-Distortion Committee Selection

We introduce a novel definition for a small set R of k points being "representative" of a larger set in a metric space. Given a set V (e.g., documents or voters) to represent, and a set C of possible representatives, our criterion requires that for any subset S comprising a theta fraction of V, the average distance of S to their best theta*k points in R should not be more than a factor gamma compared to their average distance to the best theta*k points among all of C. This definition is a strengthening of proportional fairness and core fairness, but - different from those notions - requires that large cohesive clusters be represented proportionally to their size. Since there are instances for which - unless gamma is polynomially large - no solutions exist, we study this notion in a resource augmentation framework, implicitly stating the constraints for a set R of size k as though its size were only k/alpha, for alpha > 1. Furthermore, motivated by the application to elections, we mostly focus on the "ordinal" model, where the algorithm does not learn the actual distances; instead, it learns only for each point v in V and each candidate pairs c, c' which of c, c' is closer to v. Our main result is that the Expanding Approvals Rule (EAR) of Aziz and Lee is (alpha, gamma) representative with gamma <= 1 + 6.71 * (alpha)/(alpha-1). Our results lead to three notable byproducts. First, we show that the EAR achieves constant proportional fairness in the ordinal model, giving the first positive result on metric proportional fairness with ordinal information. Second, we show that for the core fairness objective, the EAR achieves the same asymptotic tradeoff between resource augmentation and approximation as the recent results of Li et al., which used full knowledge of the metric. Finally, our results imply a very simple single-winner voting rule with metric distortion at most 44.

Fairness in Matching under Uncertainty

The prevalence and importance of algorithmic two-sided marketplaces has drawn attention to the issue of fairness in such settings. Algorithmic decisions are used in assigning students to schools, users to advertisers, and applicants to job interviews. These decisions should heed the preferences of individuals, and simultaneously be fair with respect to their merits (synonymous with fit, future performance, or need). Merits conditioned on observable features are always uncertain, a fact that is exacerbated by the widespread use of machine learning algorithms to infer merit from the observables. As our key contribution, we carefully axiomatize a notion of individual fairness in the two-sided marketplace setting which respects the uncertainty in the merits; indeed, it simultaneously recognizes uncertainty as the primary potential cause of unfairness and an approach to address it. We design a linear programming framework to find fair utility-maximizing distributions over allocations, and we show that the linear program is robust to perturbations in the estimated parameters of the uncertain merit distributions, a key property in combining the approach with machine learning techniques.

Active Learning for Non-Parametric Choice Models

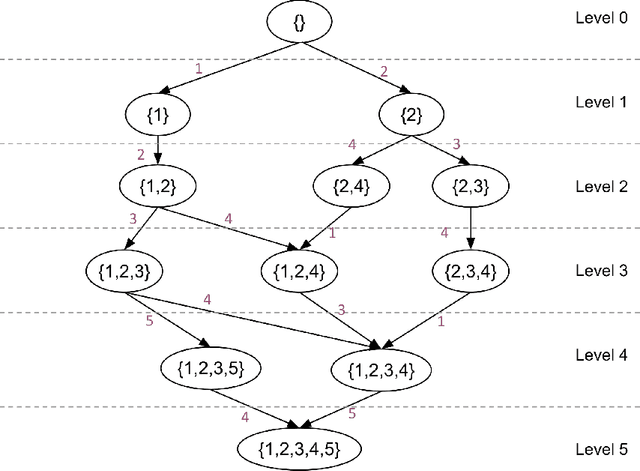
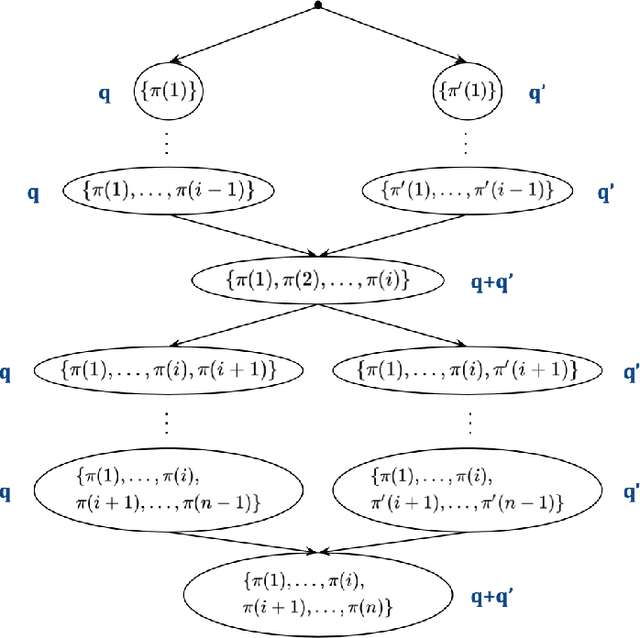
We study the problem of actively learning a non-parametric choice model based on consumers' decisions. We present a negative result showing that such choice models may not be identifiable. To overcome the identifiability problem, we introduce a directed acyclic graph (DAG) representation of the choice model, which in a sense captures as much information about the choice model as could information-theoretically be identified. We then consider the problem of learning an approximation to this DAG representation in an active-learning setting. We design an efficient active-learning algorithm to estimate the DAG representation of the non-parametric choice model, which runs in polynomial time when the set of frequent rankings is drawn uniformly at random. Our algorithm learns the distribution over the most popular items of frequent preferences by actively and repeatedly offering assortments of items and observing the item chosen. We show that our algorithm can better recover a set of frequent preferences on both a synthetic and publicly available dataset on consumers' preferences, compared to the corresponding non-active learning estimation algorithms. This demonstrates the value of our algorithm and active-learning approaches more generally.

Plurality Veto: A Simple Voting Rule Achieving Optimal Metric Distortion

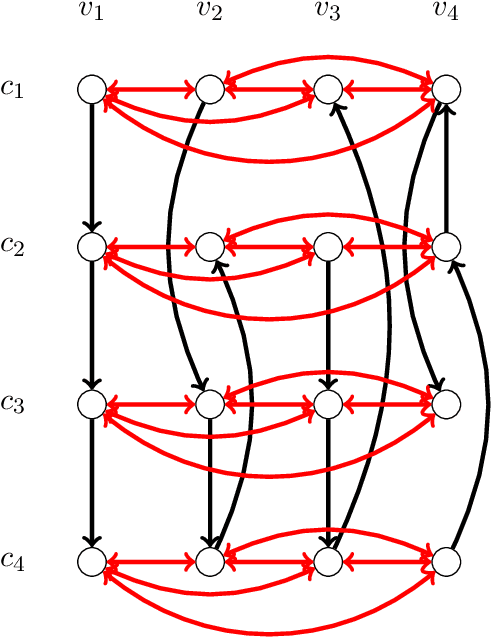
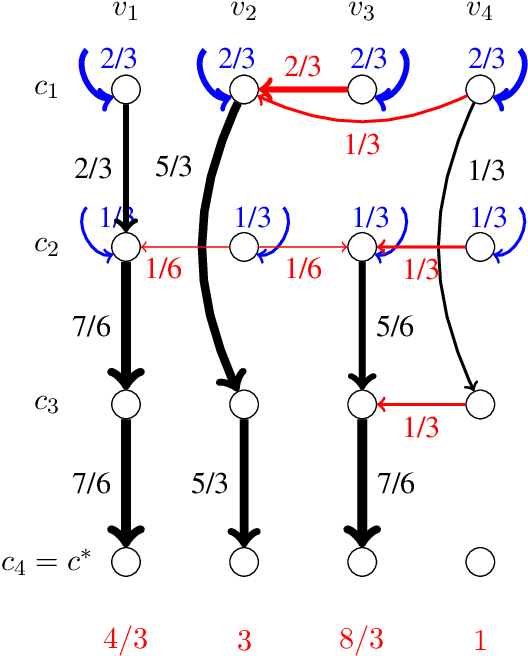
The metric distortion framework posits that n voters and m candidates are jointly embedded in a metric space such that voters rank candidates that are closer to them higher. A voting rule's purpose is to pick a candidate with minimum total distance to the voters, given only the rankings, but not the actual distances. As a result, in the worst case, each deterministic rule picks a candidate whose total distance is at least three times larger than that of an optimal one, i.e., has distortion at least 3. A recent breakthrough result showed that achieving this bound of 3 is possible; however, the proof is non-constructive, and the voting rule itself is a complicated exhaustive search. Our main result is an extremely simple voting rule, called Plurality Veto, which achieves the same optimal distortion of 3. Each candidate starts with a score equal to his number of first-place votes. These scores are then gradually decreased via an n-round veto process in which a candidate drops out when his score reaches zero. One after the other, voters decrement the score of their bottom choice among the standing candidates, and the last standing candidate wins. We give a one-paragraph proof that this voting rule achieves distortion 3. This rule is also immensely practical, and it only makes two queries to each voter, so it has low communication overhead. We also generalize Plurality Veto into a class of randomized voting rules in the following way: Plurality veto is run only for k < n rounds; then, a candidate is chosen with probability proportional to his residual score. This general rule interpolates between Random Dictatorship (for k=0) and Plurality Veto (for k=n-1), and k controls the variance of the output. We show that for all k, this rule has distortion at most 3.

Networked Restless Multi-Armed Bandits for Mobile Interventions

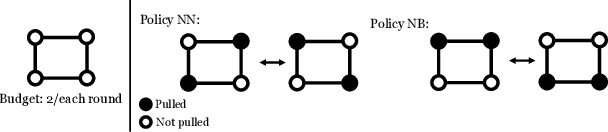
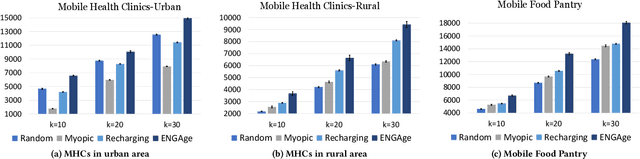
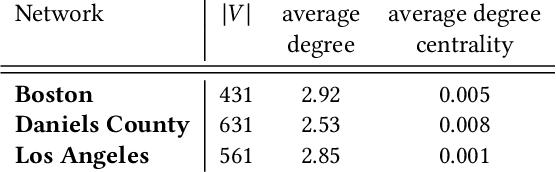
Motivated by a broad class of mobile intervention problems, we propose and study restless multi-armed bandits (RMABs) with network effects. In our model, arms are partially recharging and connected through a graph, so that pulling one arm also improves the state of neighboring arms, significantly extending the previously studied setting of fully recharging bandits with no network effects. In mobile interventions, network effects may arise due to regular population movements (such as commuting between home and work). We show that network effects in RMABs induce strong reward coupling that is not accounted for by existing solution methods. We propose a new solution approach for networked RMABs, exploiting concavity properties which arise under natural assumptions on the structure of intervention effects. We provide sufficient conditions for optimality of our approach in idealized settings and demonstrate that it empirically outperforms state-of-the art baselines in three mobile intervention domains using real-world graphs.

Fairness in Ranking under Uncertainty

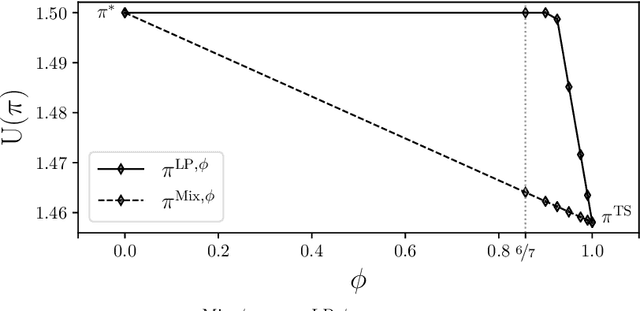
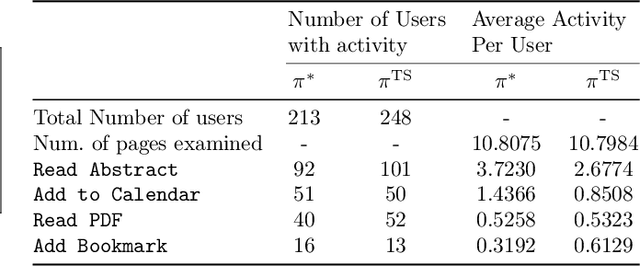
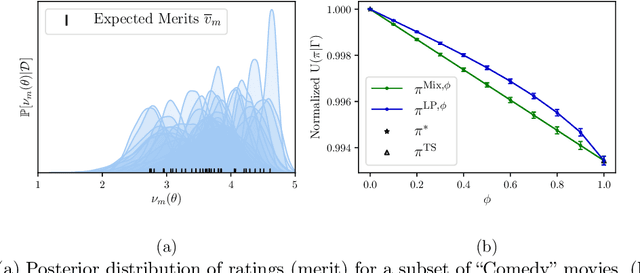
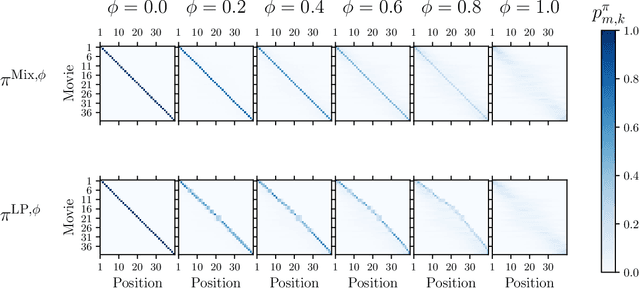
Fairness has emerged as an important consideration in algorithmic decision-making. Unfairness occurs when an agent with higher merit obtains a worse outcome than an agent with lower merit. Our central point is that a primary cause of unfairness is uncertainty. A principal or algorithm making decisions never has access to the agents' true merit, and instead uses proxy features that only imperfectly predict merit (e.g., GPA, star ratings, recommendation letters). None of these ever fully capture an agent's merit; yet existing approaches have mostly been defining fairness notions directly based on observed features and outcomes. Our primary point is that it is more principled to acknowledge and model the uncertainty explicitly. The role of observed features is to give rise to a posterior distribution of the agents' merits. We use this viewpoint to define a notion of approximate fairness in ranking. We call an algorithm $\phi$-fair (for $\phi \in [0,1]$) if it has the following property for all agents $x$ and all $k$: if agent $x$ is among the top $k$ agents with respect to merit with probability at least $\rho$ (according to the posterior merit distribution), then the algorithm places the agent among the top $k$ agents in its ranking with probability at least $\phi \rho$. We show how to compute rankings that optimally trade off approximate fairness against utility to the principal. In addition to the theoretical characterization, we present an empirical analysis of the potential impact of the approach in simulation studies. For real-world validation, we applied the approach in the context of a paper recommendation system that we built and fielded at a large conference.

Altruism Design in Networked Public Goods Games

Many collective decision-making settings feature a strategic tension between agents acting out of individual self-interest and promoting a common good. These include wearing face masks during a pandemic, voting, and vaccination. Networked public goods games capture this tension, with networks encoding strategic interdependence among agents. Conventional models of public goods games posit solely individual self-interest as a motivation, even though altruistic motivations have long been known to play a significant role in agents' decisions. We introduce a novel extension of public goods games to account for altruistic motivations by adding a term in the utility function that incorporates the perceived benefits an agent obtains from the welfare of others, mediated by an altruism graph. Most importantly, we view altruism not as immutable, but rather as a lever for promoting the common good. Our central algorithmic question then revolves around the computational complexity of modifying the altruism network to achieve desired public goods game investment profiles. We first show that the problem can be solved using linear programming when a principal can fractionally modify the altruism network. While the problem becomes in general intractable if the principal's actions are all-or-nothing, we exhibit several tractable special cases.

Adversarial Online Learning with Changing Action Sets: Efficient Algorithms with Approximate Regret Bounds

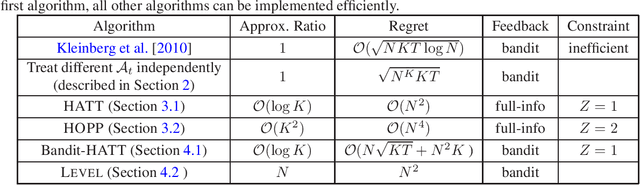
We revisit the problem of online learning with sleeping experts/bandits: in each time step, only a subset of the actions are available for the algorithm to choose from (and learn about). The work of Kleinberg et al. [2010] showed that there exist no-regret algorithms which perform no worse than the best ranking of actions asymptotically. Unfortunately, achieving this regret bound appears computationally hard: Kanade and Steinke [2014] showed that achieving this no-regret performance is at least as hard as PAC-learning DNFs, a notoriously difficult problem. In the present work, we relax the original problem and study computationally efficient no-approximate-regret algorithms: such algorithms may exceed the optimal cost by a multiplicative constant in addition to the additive regret. We give an algorithm that provides a no-approximate-regret guarantee for the general sleeping expert/bandit problems. For several canonical special cases of the problem, we give algorithms with significantly better approximation ratios; these algorithms also illustrate different techniques for achieving no-approximate-regret guarantees.