Polynomial-Time Relational Probabilistic Inference in Open Universes

Reasoning under uncertainty is a fundamental challenge in Artificial Intelligence. As with most of these challenges, there is a harsh dilemma between the expressive power of the language used, and the tractability of the computational problem posed by reasoning. Inspired by human reasoning, we introduce a method of first-order relational probabilistic inference that satisfies both criteria, and can handle hybrid (discrete and continuous) variables. Specifically, we extend sum-of-squares logic of expectation to relational settings, demonstrating that lifted reasoning in the bounded-degree fragment for knowledge bases of bounded quantifier rank can be performed in polynomial time, even with an a priori unknown and/or countably infinite set of objects. Crucially, our notion of tractability is framed in proof-theoretic terms, which extends beyond the syntactic properties of the language or queries. We are able to derive the tightest bounds provable by proofs of a given degree and size and establish completeness in our sum-of-squares refutations for fixed degrees.

Learning Linear Utility Functions From Pairwise Comparison Queries

We study learnability of linear utility functions from pairwise comparison queries. In particular, we consider two learning objectives. The first objective is to predict out-of-sample responses to pairwise comparisons, whereas the second is to approximately recover the true parameters of the utility function. We show that in the passive learning setting, linear utilities are efficiently learnable with respect to the first objective, both when query responses are uncorrupted by noise, and under Tsybakov noise when the distributions are sufficiently "nice". In contrast, we show that utility parameters are not learnable for a large set of data distributions without strong modeling assumptions, even when query responses are noise-free. Next, we proceed to analyze the learning problem in an active learning setting. In this case, we show that even the second objective is efficiently learnable, and present algorithms for both the noise-free and noisy query response settings. Our results thus exhibit a qualitative learnability gap between passive and active learning from pairwise preference queries, demonstrating the value of the ability to select pairwise queries for utility learning.

Safe Learning of PDDL Domains with Conditional Effects -- Extended Version

Powerful domain-independent planners have been developed to solve various types of planning problems. These planners often require a model of the acting agent's actions, given in some planning domain description language. Manually designing such an action model is a notoriously challenging task. An alternative is to automatically learn action models from observation. Such an action model is called safe if every plan created with it is consistent with the real, unknown action model. Algorithms for learning such safe action models exist, yet they cannot handle domains with conditional or universal effects, which are common constructs in many planning problems. We prove that learning non-trivial safe action models with conditional effects may require an exponential number of samples. Then, we identify reasonable assumptions under which such learning is tractable and propose SAM Learning of Conditional Effects (Conditional-SAM), the first algorithm capable of doing so. We analyze Conditional-SAM theoretically and evaluate it experimentally. Our results show that the action models learned by Conditional-SAM can be used to solve perfectly most of the test set problems in most of the experimented domains.

Polynomial time auditing of statistical subgroup fairness for Gaussian data

We study the problem of auditing classifiers with the notion of statistical subgroup fairness. Kearns et al. (2018) has shown that the problem of auditing combinatorial subgroups fairness is as hard as agnostic learning. Essentially all work on remedying statistical measures of discrimination against subgroups assumes access to an oracle for this problem, despite the fact that no efficient algorithms are known for it. If we assume the data distribution is Gaussian, or even merely log-concave, then a recent line of work has discovered efficient agnostic learning algorithms for halfspaces. Unfortunately, the boosting-style reductions given by Kearns et al. required the agnostic learning algorithm to succeed on reweighted distributions that may not be log-concave, even if the original data distribution was. In this work, we give positive and negative results on auditing for the Gaussian distribution: On the positive side, we an alternative approach to leverage these advances in agnostic learning and thereby obtain the first polynomial-time approximation scheme (PTAS) for auditing nontrivial combinatorial subgroup fairness: we show how to audit statistical notions of fairness over homogeneous halfspace subgroups when the features are Gaussian. On the negative side, we find that under cryptographic assumptions, no polynomial-time algorithm can guarantee any nontrivial auditing, even under Gaussian feature distributions, for general halfspace subgroups.

Learnability with PAC Semantics for Multi-agent Beliefs

The tension between deduction and induction is perhaps the most fundamental issue in areas such as philosophy, cognition and artificial intelligence. In an influential paper, Valiant recognised that the challenge of learning should be integrated with deduction. In particular, he proposed a semantics to capture the quality possessed by the output of Probably Approximately Correct (PAC) learning algorithms when formulated in a logic. Although weaker than classical entailment, it allows for a powerful model-theoretic framework for answering queries. In this paper, we provide a new technical foundation to demonstrate PAC learning with multi-agent epistemic logics. To circumvent the negative results in the literature on the difficulty of robust learning with the PAC semantics, we consider so-called implicit learning where we are able to incorporate observations to the background theory in service of deciding the entailment of an epistemic query. We prove correctness of the learning procedure and discuss results on the sample complexity, that is how many observations we will need to provably assert that the query is entailed given a user-specified error bound. Finally, we investigate under what circumstances this algorithm can be made efficient. On the last point, given that reasoning in epistemic logics especially in multi-agent epistemic logics is PSPACE-complete, it might seem like there is no hope for this problem. We leverage some recent results on the so-called Representation Theorem explored for single-agent and multi-agent epistemic logics with the only knowing operator to reduce modal reasoning to propositional reasoning.

Hardness of Maximum Likelihood Learning of DPPs

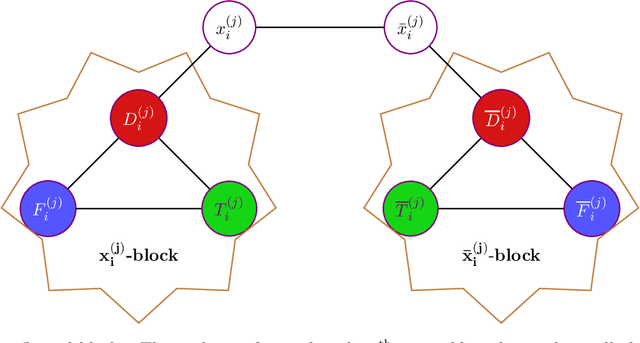
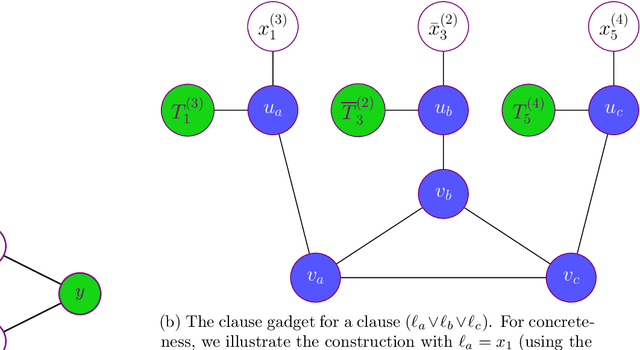
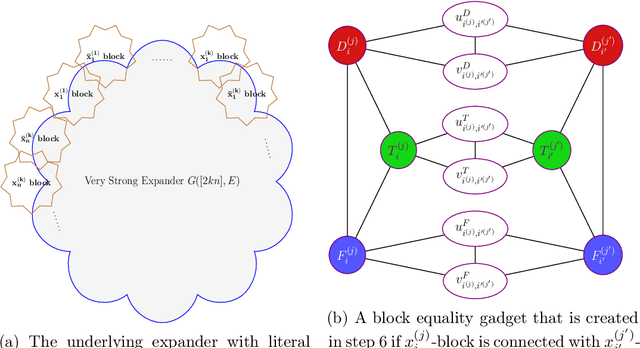
Determinantal Point Processes (DPPs) are a widely used probabilistic model for negatively correlated sets. DPPs have been successfully employed in Machine Learning applications to select a diverse, yet representative subset of data. In seminal work on DPPs in Machine Learning, Kulesza conjectured in his PhD Thesis (2011) that the problem of finding a maximum likelihood DPP model for a given data set is NP-complete. In this work we prove Kulesza's conjecture. In fact, we prove the following stronger hardness of approximation result: even computing a $\left(1-O(\frac{1}{\log^9{N}})\right)$-approximation to the maximum log-likelihood of a DPP on a ground set of $N$ elements is NP-complete. At the same time, we also obtain the first polynomial-time algorithm that achieves a nontrivial worst-case approximation to the optimal log-likelihood: the approximation factor is $\frac{1}{(1+o(1))\log{m}}$ unconditionally (for data sets that consist of $m$ subsets), and can be improved to $1-\frac{1+o(1)}{\log N}$ if all $N$ elements appear in a $O(1/N)$-fraction of the subsets. In terms of techniques, we reduce approximating the maximum log-likelihood of DPPs on a data set to solving a gap instance of a "vector coloring" problem on a hypergraph. Such a hypergraph is built on a bounded-degree graph construction of Bogdanov, Obata and Trevisan (FOCS 2002), and is further enhanced by the strong expanders of Alon and Capalbo (FOCS 2007) to serve our purposes.

An Example of the SAM+ Algorithm for Learning Action Models for Stochastic Worlds

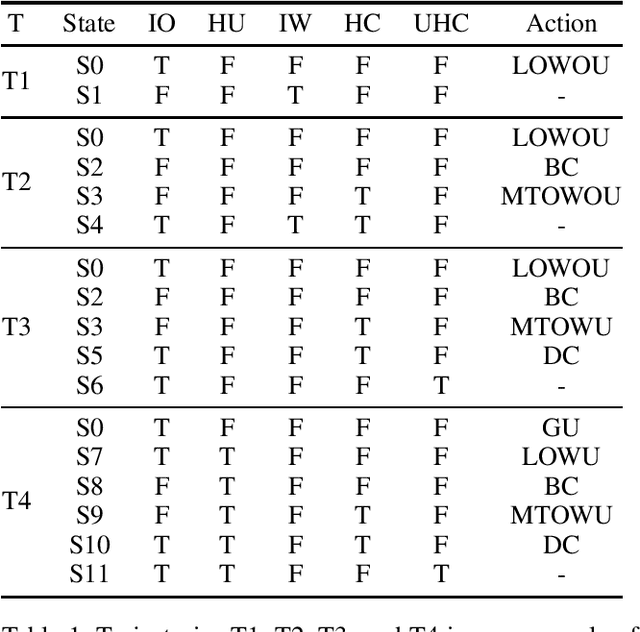
In this technical report, we provide a complete example of running the SAM+ algorithm, an algorithm for learning stochastic planning action models, on a simplified PPDDL version of the Coffee problem. We provide a very brief description of the SAM+ algorithm and detailed description of our simplified version of the Coffee domain, and then describe the results of running it on the simplified Coffee domain.

Provable Hierarchical Lifelong Learning with a Sketch-based Modular Architecture

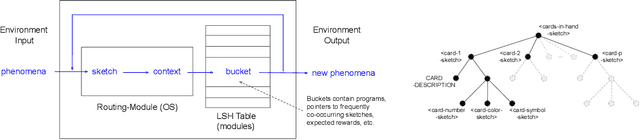
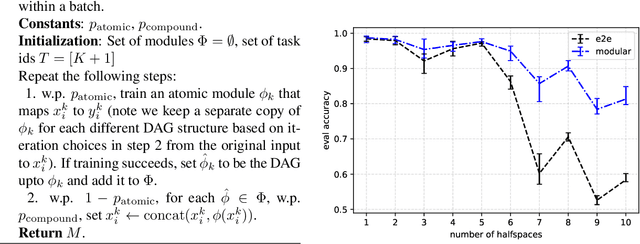
We propose a modular architecture for the lifelong learning of hierarchically structured tasks. Specifically, we prove that our architecture is theoretically able to learn tasks that can be solved by functions that are learnable given access to functions for other, previously learned tasks as subroutines. We empirically show that some tasks that we can learn in this way are not learned by standard training methods in practice; indeed, prior work suggests that some such tasks cannot be learned by any efficient method without the aid of the simpler tasks. We also consider methods for identifying the tasks automatically, without relying on explicitly given indicators.

Conditional Linear Regression for Heterogeneous Covariances

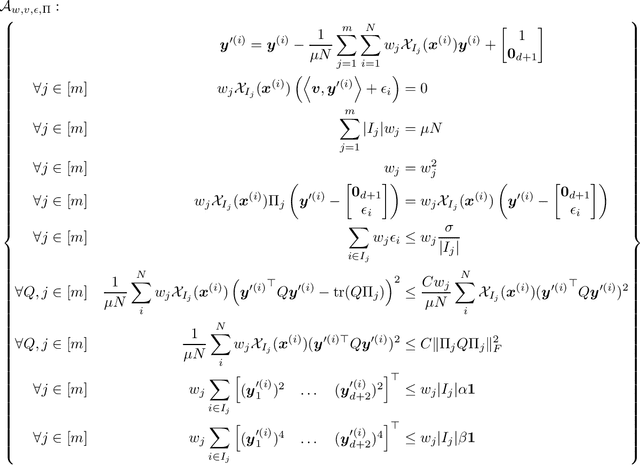
Often machine learning and statistical models will attempt to describe the majority of the data. However, there may be situations where only a fraction of the data can be fit well by a linear regression model. Here, we are interested in a case where such inliers can be identified by a Disjunctive Normal Form (DNF) formula. We give a polynomial time algorithm for the conditional linear regression task, which identifies a DNF condition together with the linear predictor on the corresponding portion of the data. In this work, we improve on previous algorithms by removing a requirement that the covariances of the data satisfying each of the terms of the condition have to all be very similar in spectral norm to the covariance of the overall condition.

Polynomial Time Reinforcement Learning in Correlated FMDPs with Linear Value Functions

Many reinforcement learning (RL) environments in practice feature enormous state spaces that may be described compactly by a "factored" structure, that may be modeled by Factored Markov Decision Processes (FMDPs). We present the first polynomial-time algorithm for RL with FMDPs that does not rely on an oracle planner, and instead of requiring a linear transition model, only requires a linear value function with a suitable local basis with respect to the factorization. With this assumption, we can solve FMDPs in polynomial time by constructing an efficient separation oracle for convex optimization. Importantly, and in contrast to prior work, we do not assume that the transitions on various factors are independent.