Inductive Biases and Variable Creation in Self-Attention Mechanisms

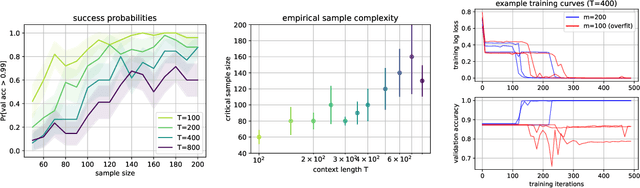
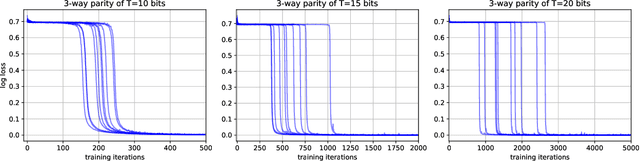
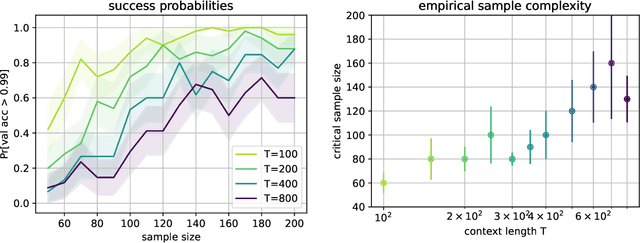
Self-attention, an architectural motif designed to model long-range interactions in sequential data, has driven numerous recent breakthroughs in natural language processing and beyond. This work provides a theoretical analysis of the inductive biases of self-attention modules, where our focus is to rigorously establish which functions and long-range dependencies self-attention blocks prefer to represent. Our main result shows that bounded-norm Transformer layers create sparse variables: they can represent sparse functions of the input sequence, with sample complexity scaling only logarithmically with the context length. Furthermore, we propose new experimental protocols to support this analysis and to guide the practice of training Transformers, built around the large body of work on provably learning sparse Boolean functions.

Sparsity in Partially Controllable Linear Systems

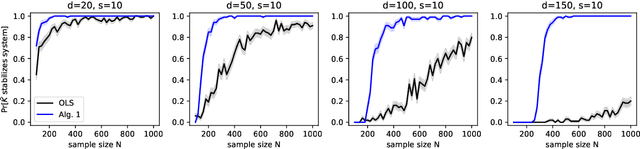
A fundamental concept in control theory is that of controllability, where any system state can be reached through an appropriate choice of control inputs. Indeed, a large body of classical and modern approaches are designed for controllable linear dynamical systems. However, in practice, we often encounter systems in which a large set of state variables evolve exogenously and independently of the control inputs; such systems are only \emph{partially controllable}. The focus of this work is on a large class of partially controllable linear dynamical systems, specified by an underlying sparsity pattern. Our main results establish structural conditions and finite-sample guarantees for learning to control such systems. In particular, our structural results characterize those state variables which are irrelevant for optimal control, an analysis which departs from classical control techniques. Our algorithmic results adapt techniques from high-dimensional statistics -- specifically soft-thresholding and semiparametric least-squares -- to exploit the underlying sparsity pattern in order to obtain finite-sample guarantees that significantly improve over those based on certainty-equivalence. We also corroborate these theoretical improvements over certainty-equivalent control through a simulation study.

Koopman Spectrum Nonlinear Regulator and Provably Efficient Online Learning

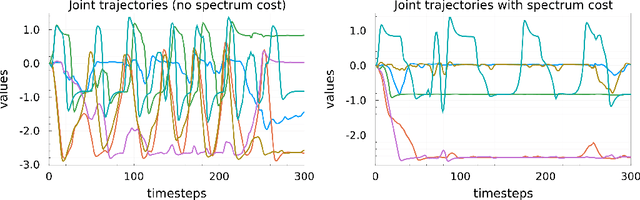
Most modern reinforcement learning algorithms optimize a cumulative single-step cost along a trajectory. The optimized motions are often 'unnatural', representing, for example, behaviors with sudden accelerations that waste energy and lack predictability. In this work, we present a novel paradigm of controlling nonlinear systems via the minimization of the Koopman spectrum cost: a cost over the Koopman operator of the controlled dynamics. This induces a broader class of dynamical behaviors that evolve over stable manifolds such as nonlinear oscillators, closed loops, and smooth movements. We demonstrate that some dynamics realizations that are not possible with a cumulative cost are feasible in this paradigm. Moreover, we present a provably efficient online learning algorithm for our problem that enjoys a sub-linear regret bound under some structural assumptions.

Gone Fishing: Neural Active Learning with Fisher Embeddings

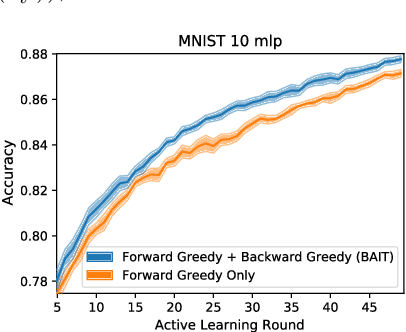
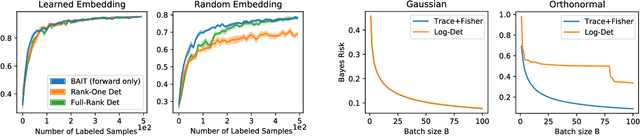
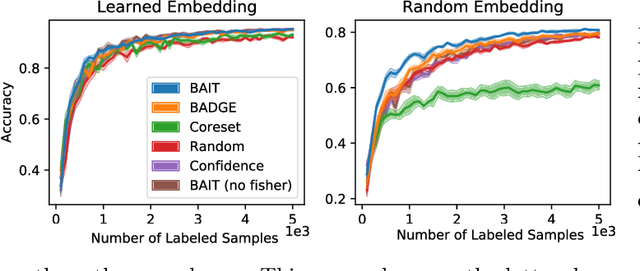
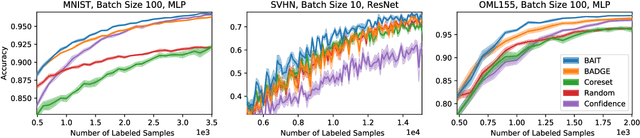
There is an increasing need for effective active learning algorithms that are compatible with deep neural networks. While there are many classic, well-studied sample selection methods, the non-convexity and varying internal representation of neural models make it unclear how to extend these approaches. This article introduces BAIT, a practical, tractable, and high-performing active learning algorithm for neural networks that addresses these concerns. BAIT draws inspiration from the theoretical analysis of maximum likelihood estimators (MLE) for parametric models. It selects batches of samples by optimizing a bound on the MLE error in terms of the Fisher information, which we show can be implemented efficiently at scale by exploiting linear-algebraic structure especially amenable to execution on modern hardware. Our experiments show that BAIT outperforms the previous state of the art on both classification and regression problems, and is flexible enough to be used with a variety of model architectures.

LLC: Accurate, Multi-purpose Learnt Low-dimensional Binary Codes

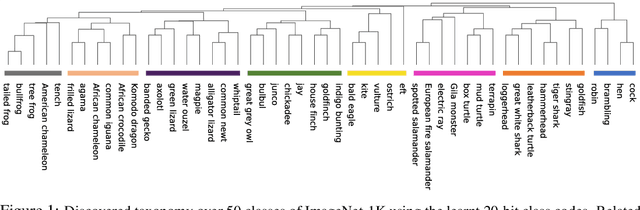
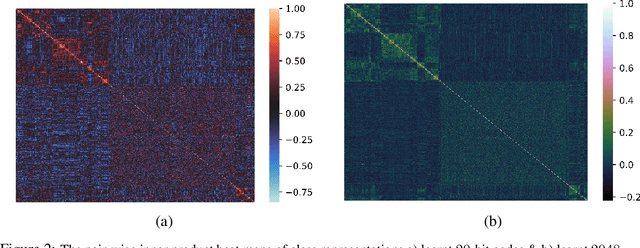
Learning binary representations of instances and classes is a classical problem with several high potential applications. In modern settings, the compression of high-dimensional neural representations to low-dimensional binary codes is a challenging task and often require large bit-codes to be accurate. In this work, we propose a novel method for Learning Low-dimensional binary Codes (LLC) for instances as well as classes. Our method does not require any side-information, like annotated attributes or label meta-data, and learns extremely low-dimensional binary codes (~20 bits for ImageNet-1K). The learnt codes are super-efficient while still ensuring nearly optimal classification accuracy for ResNet50 on ImageNet-1K. We demonstrate that the learnt codes capture intrinsically important features in the data, by discovering an intuitive taxonomy over classes. We further quantitatively measure the quality of our codes by applying it to the efficient image retrieval as well as out-of-distribution (OOD) detection problems. For ImageNet-100 retrieval problem, our learnt binary codes outperform 16 bit HashNet using only 10 bits and also are as accurate as 10 dimensional real representations. Finally, our learnt binary codes can perform OOD detection, out-of-the-box, as accurately as a baseline that needs ~3000 samples to tune its threshold, while we require none. Code and pre-trained models are available at https://github.com/RAIVNLab/LLC.

Robust and Differentially Private Mean Estimation

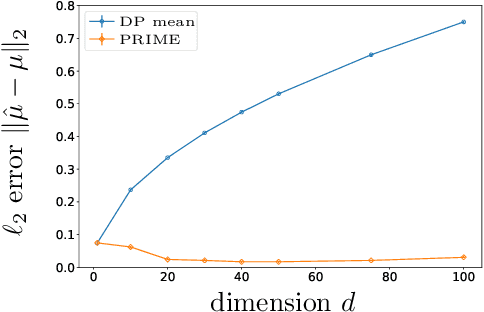
Differential privacy has emerged as a standard requirement in a variety of applications ranging from the U.S. Census to data collected in commercial devices, initiating an extensive line of research in accurately and privately releasing statistics of a database. An increasing number of such databases consist of data from multiple sources, not all of which can be trusted. This leaves existing private analyses vulnerable to attacks by an adversary who injects corrupted data. Despite the significance of designing algorithms that guarantee privacy and robustness (to a fraction of data being corrupted) simultaneously, even the simplest questions remain open. For the canonical problem of estimating the mean from i.i.d. samples, we introduce the first efficient algorithm that achieves both privacy and robustness for a wide range of distributions. This achieves optimal accuracy matching the known lower bounds for robustness, but the sample complexity has a factor of $d^{1/2}$ gap from known lower bounds. We further show that this gap is due to the computational efficiency; we introduce the first family of algorithms that close this gap but takes exponential time. The innovation is in exploiting resilience (a key property in robust estimation) to adaptively bound the sensitivity and improve privacy.

How Important is the Train-Validation Split in Meta-Learning?

Meta-learning aims to perform fast adaptation on a new task through learning a "prior" from multiple existing tasks. A common practice in meta-learning is to perform a train-validation split where the prior adapts to the task on one split of the data, and the resulting predictor is evaluated on another split. Despite its prevalence, the importance of the train-validation split is not well understood either in theory or in practice, particularly in comparison to the more direct non-splitting method, which uses all the per-task data for both training and evaluation. We provide a detailed theoretical study on whether and when the train-validation split is helpful on the linear centroid meta-learning problem, in the asymptotic setting where the number of tasks goes to infinity. We show that the splitting method converges to the optimal prior as expected, whereas the non-splitting method does not in general without structural assumptions on the data. In contrast, if the data are generated from linear models (the realizable regime), we show that both the splitting and non-splitting methods converge to the optimal prior. Further, perhaps surprisingly, our main result shows that the non-splitting method achieves a strictly better asymptotic excess risk under this data distribution, even when the regularization parameter and split ratio are optimally tuned for both methods. Our results highlight that data splitting may not always be preferable, especially when the data is realizable by the model. We validate our theories by experimentally showing that the non-splitting method can indeed outperform the splitting method, on both simulations and real meta-learning tasks.

PC-PG: Policy Cover Directed Exploration for Provable Policy Gradient Learning

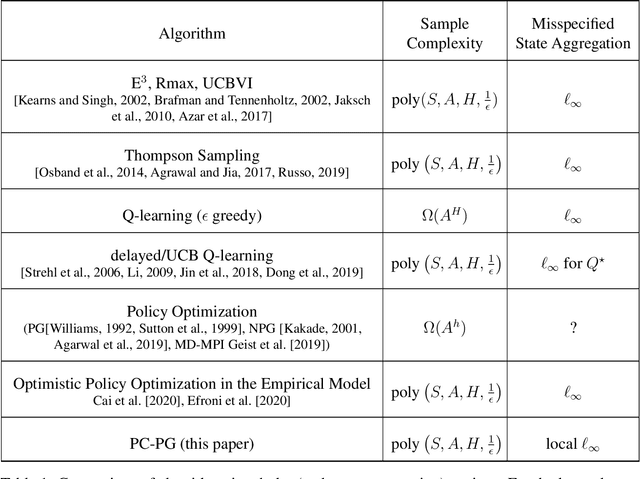
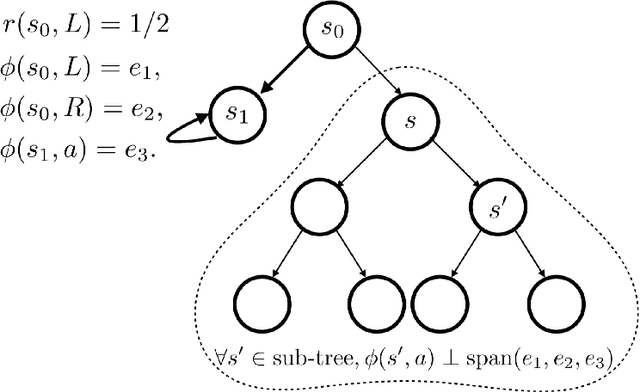
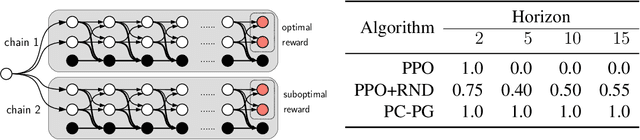
Direct policy gradient methods for reinforcement learning are a successful approach for a variety of reasons: they are model free, they directly optimize the performance metric of interest, and they allow for richly parameterized policies. Their primary drawback is that, by being local in nature, they fail to adequately explore the environment. In contrast, while model-based approaches and Q-learning directly handle exploration through the use of optimism, their ability to handle model misspecification and function approximation is far less evident. This work introduces the the Policy Cover-Policy Gradient (PC-PG) algorithm, which provably balances the exploration vs. exploitation tradeoff using an ensemble of learned policies (the policy cover). PC-PG enjoys polynomial sample complexity and run time for both tabular MDPs and, more generally, linear MDPs in an infinite dimensional RKHS. Furthermore, PC-PG also has strong guarantees under model misspecification that go beyond the standard worst case $\ell_{\infty}$ assumptions; this includes approximation guarantees for state aggregation under an average case error assumption, along with guarantees under a more general assumption where the approximation error under distribution shift is controlled. We complement the theory with empirical evaluation across a variety of domains in both reward-free and reward-driven settings.

Information Theoretic Regret Bounds for Online Nonlinear Control

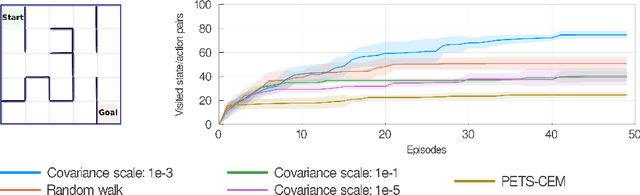
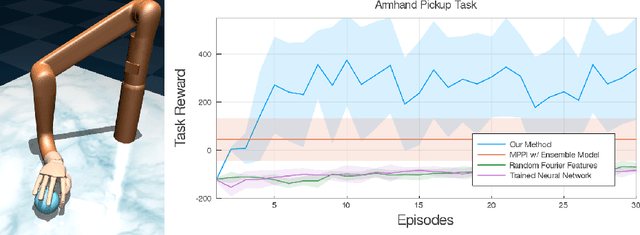
This work studies the problem of sequential control in an unknown, nonlinear dynamical system, where we model the underlying system dynamics as an unknown function in a known Reproducing Kernel Hilbert Space. This framework yields a general setting that permits discrete and continuous control inputs as well as non-smooth, non-differentiable dynamics. Our main result, the Lower Confidence-based Continuous Control ($LC^3$) algorithm, enjoys a near-optimal $O(\sqrt{T})$ regret bound against the optimal controller in episodic settings, where $T$ is the number of episodes. The bound has no explicit dependence on dimension of the system dynamics, which could be infinite, but instead only depends on information theoretic quantities. We empirically show its application to a number of nonlinear control tasks and demonstrate the benefit of exploration for learning model dynamics.

FLAMBE: Structural Complexity and Representation Learning of Low Rank MDPs

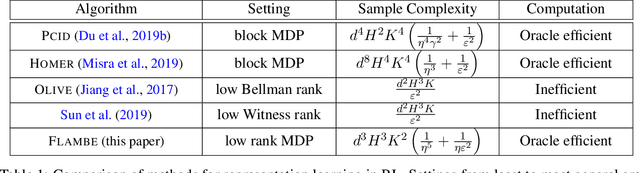
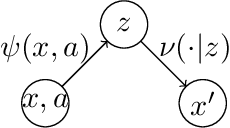
In order to deal with the curse of dimensionality in reinforcement learning (RL), it is common practice to make parametric assumptions where values or policies are functions of some low dimensional feature space. This work focuses on the representation learning question: how can we learn such features? Under the assumption that the underlying (unknown) dynamics correspond to a low rank transition matrix, we show how the representation learning question is related to a particular non-linear matrix decomposition problem. Structurally, we make precise connections between these low rank MDPs and latent variable models, showing how they significantly generalize prior formulations for representation learning in RL. Algorithmically, we develop FLAMBE, which engages in exploration and representation learning for provably efficient RL in low rank transition models.