DeepMath-Creative: A Benchmark for Evaluating Mathematical Creativity of Large Language Models

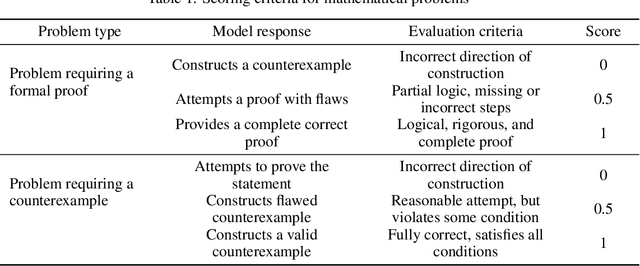
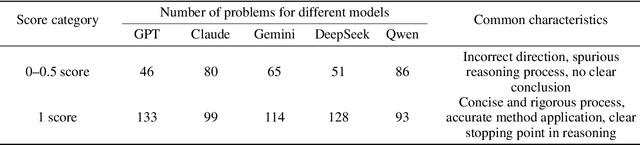
To advance the mathematical proficiency of large language models (LLMs), the DeepMath team has launched an open-source initiative aimed at developing an open mathematical LLM and systematically evaluating its mathematical creativity. This paper represents the initial contribution of this initiative. While recent developments in mathematical LLMs have predominantly emphasized reasoning skills, as evidenced by benchmarks on elementary to undergraduate-level mathematical tasks, the creative capabilities of these models have received comparatively little attention, and evaluation datasets remain scarce. To address this gap, we propose an evaluation criteria for mathematical creativity and introduce DeepMath-Creative, a novel, high-quality benchmark comprising constructive problems across algebra, geometry, analysis, and other domains. We conduct a systematic evaluation of mainstream LLMs' creative problem-solving abilities using this dataset. Experimental results show that even under lenient scoring criteria -- emphasizing core solution components and disregarding minor inaccuracies, such as small logical gaps, incomplete justifications, or redundant explanations -- the best-performing model, O3 Mini, achieves merely 70% accuracy, primarily on basic undergraduate-level constructive tasks. Performance declines sharply on more complex problems, with models failing to provide substantive strategies for open problems. These findings suggest that, although current LLMs display a degree of constructive proficiency on familiar and lower-difficulty problems, such performance is likely attributable to the recombination of memorized patterns rather than authentic creative insight or novel synthesis.

RWKV-7 "Goose" with Expressive Dynamic State Evolution

We present RWKV-7 "Goose", a new sequence modeling architecture, along with pre-trained language models that establish a new state-of-the-art in downstream performance at the 3 billion parameter scale on multilingual tasks, and match current SoTA English language performance despite being trained on dramatically fewer tokens than other top 3B models. Nevertheless, RWKV-7 models require only constant memory usage and constant inference time per token. RWKV-7 introduces a newly generalized formulation of the delta rule with vector-valued gating and in-context learning rates, as well as a relaxed value replacement rule. We show that RWKV-7 can perform state tracking and recognize all regular languages, while retaining parallelizability of training. This exceeds the capabilities of Transformers under standard complexity conjectures, which are limited to $\mathsf{TC}^0$. To demonstrate RWKV-7's language modeling capability, we also present an extended open source 3.1 trillion token multilingual corpus, and train four RWKV-7 models ranging from 0.19 billion to 2.9 billion parameters on this dataset. To foster openness, reproduction, and adoption, we release our models and dataset component listing at https://huggingface.co/RWKV, and our training and inference code at https://github.com/RWKV/RWKV-LM all under the Apache 2.0 License.

Eagle and Finch: RWKV with Matrix-Valued States and Dynamic Recurrence

We present Eagle (RWKV-5) and Finch (RWKV-6), sequence models improving upon the RWKV (RWKV-4) architecture. Our architectural design advancements include multi-headed matrix-valued states and a dynamic recurrence mechanism that improve expressivity while maintaining the inference efficiency characteristics of RNNs. We introduce a new multilingual corpus with 1.12 trillion tokens and a fast tokenizer based on greedy matching for enhanced multilinguality. We trained four Eagle models, ranging from 0.46 to 7.5 billion parameters, and two Finch models with 1.6 and 3.1 billion parameters and find that they achieve competitive performance across a wide variety of benchmarks. We release all our models on HuggingFace under the Apache 2.0 license. Models at: https://huggingface.co/RWKV Training code at: https://github.com/RWKV/RWKV-LM Inference code at: https://github.com/RWKV/ChatRWKV Time-parallel training code at: https://github.com/RWKV/RWKV-infctx-trainer

Cramer Type Distances for Learning Gaussian Mixture Models by Gradient Descent

The learning of Gaussian Mixture Models (also referred to simply as GMMs) plays an important role in machine learning. Known for their expressiveness and interpretability, Gaussian mixture models have a wide range of applications, from statistics, computer vision to distributional reinforcement learning. However, as of today, few known algorithms can fit or learn these models, some of which include Expectation-Maximization algorithms and Sliced Wasserstein Distance. Even fewer algorithms are compatible with gradient descent, the common learning process for neural networks. In this paper, we derive a closed formula of two GMMs in the univariate, one-dimensional case, then propose a distance function called Sliced Cram\'er 2-distance for learning general multivariate GMMs. Our approach has several advantages over many previous methods. First, it has a closed-form expression for the univariate case and is easy to compute and implement using common machine learning libraries (e.g., PyTorch and TensorFlow). Second, it is compatible with gradient descent, which enables us to integrate GMMs with neural networks seamlessly. Third, it can fit a GMM not only to a set of data points, but also to another GMM directly, without sampling from the target model. And fourth, it has some theoretical guarantees like global gradient boundedness and unbiased sampling gradient. These features are especially useful for distributional reinforcement learning and Deep Q Networks, where the goal is to learn a distribution over future rewards. We will also construct a Gaussian Mixture Distributional Deep Q Network as a toy example to demonstrate its effectiveness. Compared with previous models, this model is parameter efficient in terms of representing a distribution and possesses better interpretability.

RWKV: Reinventing RNNs for the Transformer Era

Transformers have revolutionized almost all natural language processing (NLP) tasks but suffer from memory and computational complexity that scales quadratically with sequence length. In contrast, recurrent neural networks (RNNs) exhibit linear scaling in memory and computational requirements but struggle to match the same performance as Transformers due to limitations in parallelization and scalability. We propose a novel model architecture, Receptance Weighted Key Value (RWKV), that combines the efficient parallelizable training of Transformers with the efficient inference of RNNs. Our approach leverages a linear attention mechanism and allows us to formulate the model as either a Transformer or an RNN, which parallelizes computations during training and maintains constant computational and memory complexity during inference, leading to the first non-transformer architecture to be scaled to tens of billions of parameters. Our experiments reveal that RWKV performs on par with similarly sized Transformers, suggesting that future work can leverage this architecture to create more efficient models. This work presents a significant step towards reconciling the trade-offs between computational efficiency and model performance in sequence processing tasks.