Learning Mixtures of Gaussians in High Dimensions

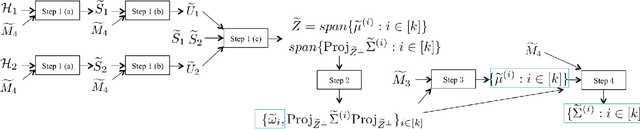
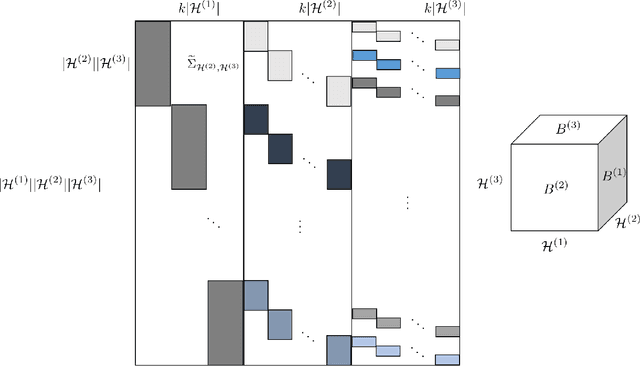
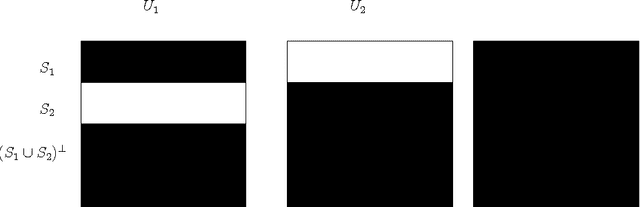
Efficiently learning mixture of Gaussians is a fundamental problem in statistics and learning theory. Given samples coming from a random one out of k Gaussian distributions in Rn, the learning problem asks to estimate the means and the covariance matrices of these Gaussians. This learning problem arises in many areas ranging from the natural sciences to the social sciences, and has also found many machine learning applications. Unfortunately, learning mixture of Gaussians is an information theoretically hard problem: in order to learn the parameters up to a reasonable accuracy, the number of samples required is exponential in the number of Gaussian components in the worst case. In this work, we show that provided we are in high enough dimensions, the class of Gaussian mixtures is learnable in its most general form under a smoothed analysis framework, where the parameters are randomly perturbed from an adversarial starting point. In particular, given samples from a mixture of Gaussians with randomly perturbed parameters, when n > {\Omega}(k^2), we give an algorithm that learns the parameters with polynomial running time and using polynomial number of samples. The central algorithmic ideas consist of new ways to decompose the moment tensor of the Gaussian mixture by exploiting its structural properties. The symmetries of this tensor are derived from the combinatorial structure of higher order moments of Gaussian distributions (sometimes referred to as Isserlis' theorem or Wick's theorem). We also develop new tools for bounding smallest singular values of structured random matrices, which could be useful in other smoothed analysis settings.

Escaping From Saddle Points --- Online Stochastic Gradient for Tensor Decomposition

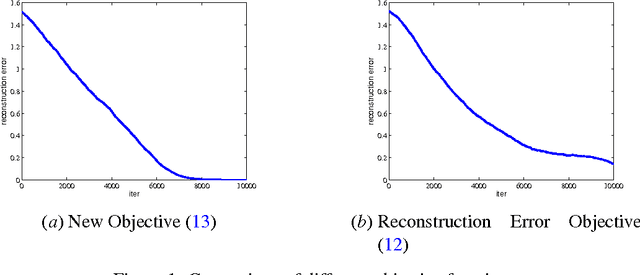
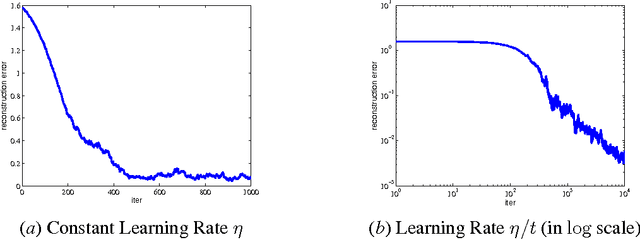
We analyze stochastic gradient descent for optimizing non-convex functions. In many cases for non-convex functions the goal is to find a reasonable local minimum, and the main concern is that gradient updates are trapped in saddle points. In this paper we identify strict saddle property for non-convex problem that allows for efficient optimization. Using this property we show that stochastic gradient descent converges to a local minimum in a polynomial number of iterations. To the best of our knowledge this is the first work that gives global convergence guarantees for stochastic gradient descent on non-convex functions with exponentially many local minima and saddle points. Our analysis can be applied to orthogonal tensor decomposition, which is widely used in learning a rich class of latent variable models. We propose a new optimization formulation for the tensor decomposition problem that has strict saddle property. As a result we get the first online algorithm for orthogonal tensor decomposition with global convergence guarantee.

Guaranteed Non-Orthogonal Tensor Decomposition via Alternating Rank-$1$ Updates

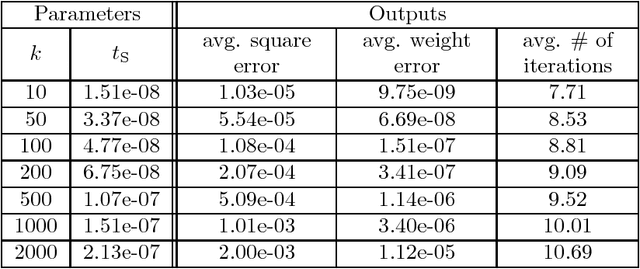
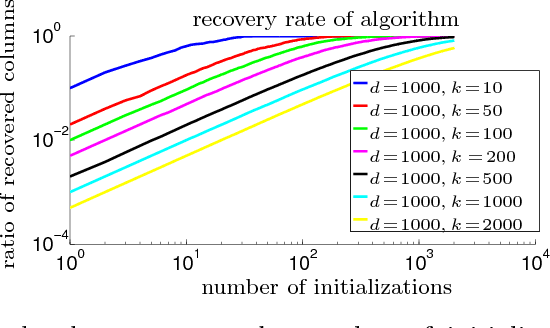
In this paper, we provide local and global convergence guarantees for recovering CP (Candecomp/Parafac) tensor decomposition. The main step of the proposed algorithm is a simple alternating rank-$1$ update which is the alternating version of the tensor power iteration adapted for asymmetric tensors. Local convergence guarantees are established for third order tensors of rank $k$ in $d$ dimensions, when $k=o \bigl( d^{1.5} \bigr)$ and the tensor components are incoherent. Thus, we can recover overcomplete tensor decomposition. We also strengthen the results to global convergence guarantees under stricter rank condition $k \le \beta d$ (for arbitrary constant $\beta > 1$) through a simple initialization procedure where the algorithm is initialized by top singular vectors of random tensor slices. Furthermore, the approximate local convergence guarantees for $p$-th order tensors are also provided under rank condition $k=o \bigl( d^{p/2} \bigr)$. The guarantees also include tight perturbation analysis given noisy tensor.

Simple, Efficient, and Neural Algorithms for Sparse Coding

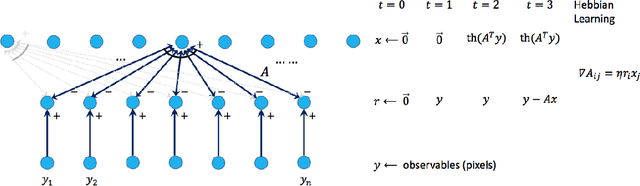
Sparse coding is a basic task in many fields including signal processing, neuroscience and machine learning where the goal is to learn a basis that enables a sparse representation of a given set of data, if one exists. Its standard formulation is as a non-convex optimization problem which is solved in practice by heuristics based on alternating minimization. Re- cent work has resulted in several algorithms for sparse coding with provable guarantees, but somewhat surprisingly these are outperformed by the simple alternating minimization heuristics. Here we give a general framework for understanding alternating minimization which we leverage to analyze existing heuristics and to design new ones also with provable guarantees. Some of these algorithms seem implementable on simple neural architectures, which was the original motivation of Olshausen and Field (1997a) in introducing sparse coding. We also give the first efficient algorithm for sparse coding that works almost up to the information theoretic limit for sparse recovery on incoherent dictionaries. All previous algorithms that approached or surpassed this limit run in time exponential in some natural parameter. Finally, our algorithms improve upon the sample complexity of existing approaches. We believe that our analysis framework will have applications in other settings where simple iterative algorithms are used.

Competing with the Empirical Risk Minimizer in a Single Pass

In many estimation problems, e.g. linear and logistic regression, we wish to minimize an unknown objective given only unbiased samples of the objective function. Furthermore, we aim to achieve this using as few samples as possible. In the absence of computational constraints, the minimizer of a sample average of observed data -- commonly referred to as either the empirical risk minimizer (ERM) or the $M$-estimator -- is widely regarded as the estimation strategy of choice due to its desirable statistical convergence properties. Our goal in this work is to perform as well as the ERM, on every problem, while minimizing the use of computational resources such as running time and space usage. We provide a simple streaming algorithm which, under standard regularity assumptions on the underlying problem, enjoys the following properties: * The algorithm can be implemented in linear time with a single pass of the observed data, using space linear in the size of a single sample. * The algorithm achieves the same statistical rate of convergence as the empirical risk minimizer on every problem, even considering constant factors. * The algorithm's performance depends on the initial error at a rate that decreases super-polynomially. * The algorithm is easily parallelizable. Moreover, we quantify the (finite-sample) rate at which the algorithm becomes competitive with the ERM.

Sample Complexity Analysis for Learning Overcomplete Latent Variable Models through Tensor Methods

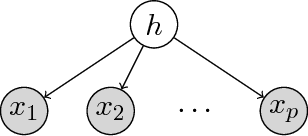
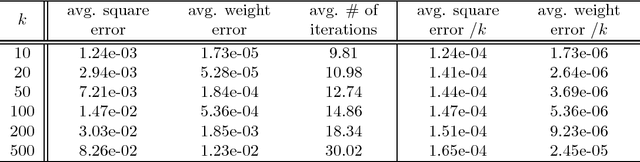
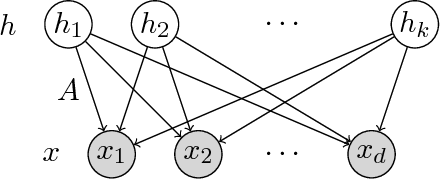
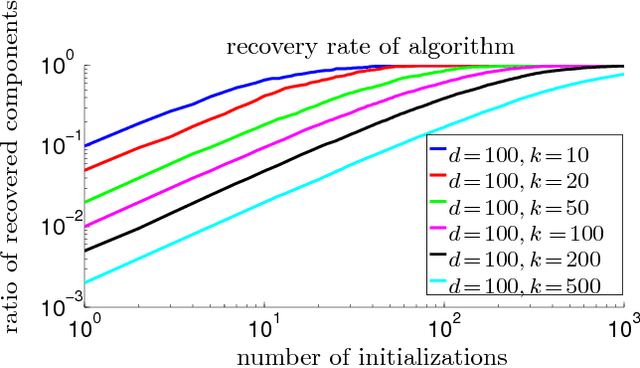
We provide guarantees for learning latent variable models emphasizing on the overcomplete regime, where the dimensionality of the latent space can exceed the observed dimensionality. In particular, we consider multiview mixtures, spherical Gaussian mixtures, ICA, and sparse coding models. We provide tight concentration bounds for empirical moments through novel covering arguments. We analyze parameter recovery through a simple tensor power update algorithm. In the semi-supervised setting, we exploit the label or prior information to get a rough estimate of the model parameters, and then refine it using the tensor method on unlabeled samples. We establish that learning is possible when the number of components scales as $k=o(d^{p/2})$, where $d$ is the observed dimension, and $p$ is the order of the observed moment employed in the tensor method. Our concentration bound analysis also leads to minimax sample complexity for semi-supervised learning of spherical Gaussian mixtures. In the unsupervised setting, we use a simple initialization algorithm based on SVD of the tensor slices, and provide guarantees under the stricter condition that $k\le \beta d$ (where constant $\beta$ can be larger than $1$), where the tensor method recovers the components under a polynomial running time (and exponential in $\beta$). Our analysis establishes that a wide range of overcomplete latent variable models can be learned efficiently with low computational and sample complexity through tensor decomposition methods.

Tensor decompositions for learning latent variable models

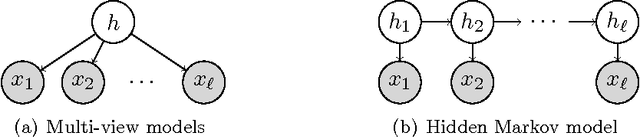
This work considers a computationally and statistically efficient parameter estimation method for a wide class of latent variable models---including Gaussian mixture models, hidden Markov models, and latent Dirichlet allocation---which exploits a certain tensor structure in their low-order observable moments (typically, of second- and third-order). Specifically, parameter estimation is reduced to the problem of extracting a certain (orthogonal) decomposition of a symmetric tensor derived from the moments; this decomposition can be viewed as a natural generalization of the singular value decomposition for matrices. Although tensor decompositions are generally intractable to compute, the decomposition of these specially structured tensors can be efficiently obtained by a variety of approaches, including power iterations and maximization approaches (similar to the case of matrices). A detailed analysis of a robust tensor power method is provided, establishing an analogue of Wedin's perturbation theorem for the singular vectors of matrices. This implies a robust and computationally tractable estimation approach for several popular latent variable models.

New Algorithms for Learning Incoherent and Overcomplete Dictionaries

In sparse recovery we are given a matrix $A$ (the dictionary) and a vector of the form $A X$ where $X$ is sparse, and the goal is to recover $X$. This is a central notion in signal processing, statistics and machine learning. But in applications such as sparse coding, edge detection, compression and super resolution, the dictionary $A$ is unknown and has to be learned from random examples of the form $Y = AX$ where $X$ is drawn from an appropriate distribution --- this is the dictionary learning problem. In most settings, $A$ is overcomplete: it has more columns than rows. This paper presents a polynomial-time algorithm for learning overcomplete dictionaries; the only previously known algorithm with provable guarantees is the recent work of Spielman, Wang and Wright who gave an algorithm for the full-rank case, which is rarely the case in applications. Our algorithm applies to incoherent dictionaries which have been a central object of study since they were introduced in seminal work of Donoho and Huo. In particular, a dictionary is $\mu$-incoherent if each pair of columns has inner product at most $\mu / \sqrt{n}$. The algorithm makes natural stochastic assumptions about the unknown sparse vector $X$, which can contain $k \leq c \min(\sqrt{n}/\mu \log n, m^{1/2 -\eta})$ non-zero entries (for any $\eta > 0$). This is close to the best $k$ allowable by the best sparse recovery algorithms even if one knows the dictionary $A$ exactly. Moreover, both the running time and sample complexity depend on $\log 1/\epsilon$, where $\epsilon$ is the target accuracy, and so our algorithms converge very quickly to the true dictionary. Our algorithm can also tolerate substantial amounts of noise provided it is incoherent with respect to the dictionary (e.g., Gaussian). In the noisy setting, our running time and sample complexity depend polynomially on $1/\epsilon$, and this is necessary.

More Algorithms for Provable Dictionary Learning

In dictionary learning, also known as sparse coding, the algorithm is given samples of the form $y = Ax$ where $x\in \mathbb{R}^m$ is an unknown random sparse vector and $A$ is an unknown dictionary matrix in $\mathbb{R}^{n\times m}$ (usually $m > n$, which is the overcomplete case). The goal is to learn $A$ and $x$. This problem has been studied in neuroscience, machine learning, visions, and image processing. In practice it is solved by heuristic algorithms and provable algorithms seemed hard to find. Recently, provable algorithms were found that work if the unknown feature vector $x$ is $\sqrt{n}$-sparse or even sparser. Spielman et al. \cite{DBLP:journals/jmlr/SpielmanWW12} did this for dictionaries where $m=n$; Arora et al. \cite{AGM} gave an algorithm for overcomplete ($m >n$) and incoherent matrices $A$; and Agarwal et al. \cite{DBLP:journals/corr/AgarwalAN13} handled a similar case but with weaker guarantees. This raised the problem of designing provable algorithms that allow sparsity $\gg \sqrt{n}$ in the hidden vector $x$. The current paper designs algorithms that allow sparsity up to $n/poly(\log n)$. It works for a class of matrices where features are individually recoverable, a new notion identified in this paper that may motivate further work. The algorithm runs in quasipolynomial time because they use limited enumeration.

A Tensor Approach to Learning Mixed Membership Community Models

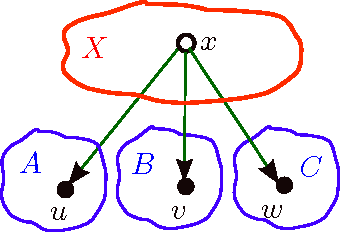
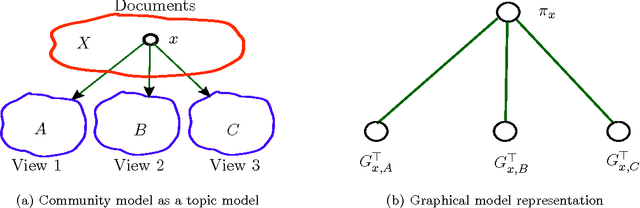
Community detection is the task of detecting hidden communities from observed interactions. Guaranteed community detection has so far been mostly limited to models with non-overlapping communities such as the stochastic block model. In this paper, we remove this restriction, and provide guaranteed community detection for a family of probabilistic network models with overlapping communities, termed as the mixed membership Dirichlet model, first introduced by Airoldi et al. This model allows for nodes to have fractional memberships in multiple communities and assumes that the community memberships are drawn from a Dirichlet distribution. Moreover, it contains the stochastic block model as a special case. We propose a unified approach to learning these models via a tensor spectral decomposition method. Our estimator is based on low-order moment tensor of the observed network, consisting of 3-star counts. Our learning method is fast and is based on simple linear algebraic operations, e.g. singular value decomposition and tensor power iterations. We provide guaranteed recovery of community memberships and model parameters and present a careful finite sample analysis of our learning method. As an important special case, our results match the best known scaling requirements for the (homogeneous) stochastic block model.