Sample Complexity Analysis for Learning Overcomplete Latent Variable Models through Tensor Methods
Paper and Code
Dec 16, 2014
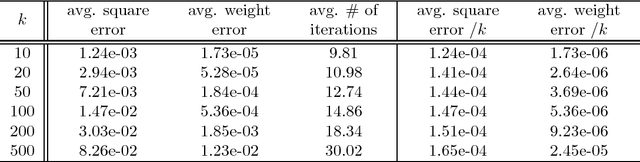
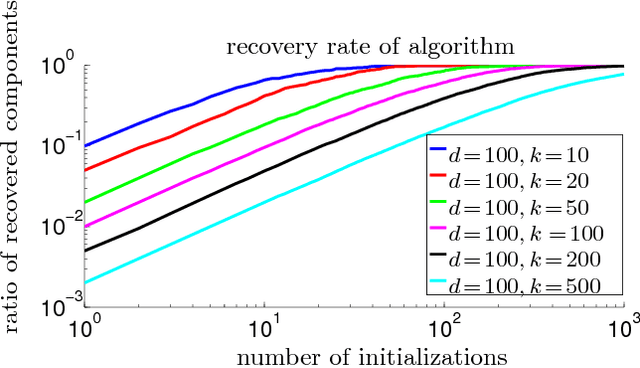
We provide guarantees for learning latent variable models emphasizing on the overcomplete regime, where the dimensionality of the latent space can exceed the observed dimensionality. In particular, we consider multiview mixtures, spherical Gaussian mixtures, ICA, and sparse coding models. We provide tight concentration bounds for empirical moments through novel covering arguments. We analyze parameter recovery through a simple tensor power update algorithm. In the semi-supervised setting, we exploit the label or prior information to get a rough estimate of the model parameters, and then refine it using the tensor method on unlabeled samples. We establish that learning is possible when the number of components scales as $k=o(d^{p/2})$, where $d$ is the observed dimension, and $p$ is the order of the observed moment employed in the tensor method. Our concentration bound analysis also leads to minimax sample complexity for semi-supervised learning of spherical Gaussian mixtures. In the unsupervised setting, we use a simple initialization algorithm based on SVD of the tensor slices, and provide guarantees under the stricter condition that $k\le \beta d$ (where constant $\beta$ can be larger than $1$), where the tensor method recovers the components under a polynomial running time (and exponential in $\beta$). Our analysis establishes that a wide range of overcomplete latent variable models can be learned efficiently with low computational and sample complexity through tensor decomposition methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge