Customizing ML Predictions for Online Algorithms

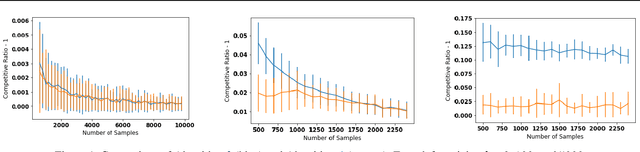
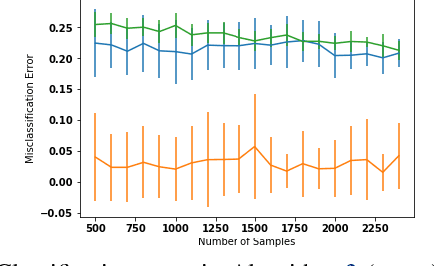
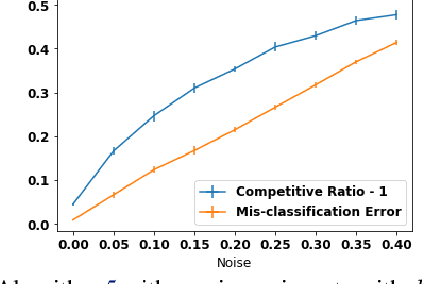
A popular line of recent research incorporates ML advice in the design of online algorithms to improve their performance in typical instances. These papers treat the ML algorithm as a black-box, and redesign online algorithms to take advantage of ML predictions. In this paper, we ask the complementary question: can we redesign ML algorithms to provide better predictions for online algorithms? We explore this question in the context of the classic rent-or-buy problem, and show that incorporating optimization benchmarks in ML loss functions leads to significantly better performance, while maintaining a worst-case adversarial result when the advice is completely wrong. We support this finding both through theoretical bounds and numerical simulations.

Online Algorithms with Multiple Predictions

This paper studies online algorithms augmented with multiple machine-learned predictions. While online algorithms augmented with a single prediction have been extensively studied in recent years, the literature for the multiple predictions setting is sparse. In this paper, we give a generic algorithmic framework for online covering problems with multiple predictions that obtains an online solution that is competitive against the performance of the best predictor. Our algorithm incorporates the use of predictions in the classic potential-based analysis of online algorithms. We apply our algorithmic framework to solve classical problems such as online set cover, (weighted) caching, and online facility location in the multiple predictions setting. Our algorithm can also be robustified, i.e., the algorithm can be simultaneously made competitive against the best prediction and the performance of the best online algorithm (without prediction).

Towards Understanding the Data Dependency of Mixup-style Training

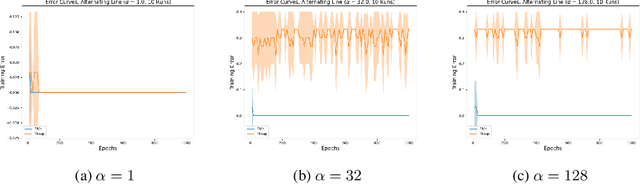
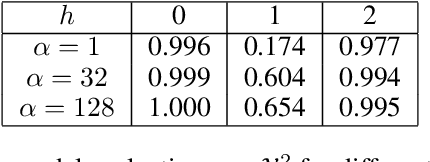
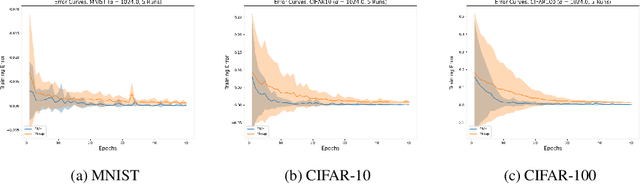
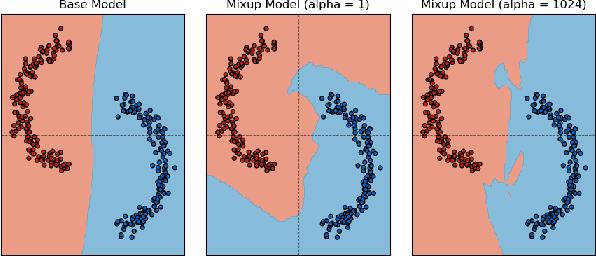
In the Mixup training paradigm, a model is trained using convex combinations of data points and their associated labels. Despite seeing very few true data points during training, models trained using Mixup seem to still minimize the original empirical risk and exhibit better generalization and robustness on various tasks when compared to standard training. In this paper, we investigate how these benefits of Mixup training rely on properties of the data in the context of classification. For minimizing the original empirical risk, we compute a closed form for the Mixup-optimal classification, which allows us to construct a simple dataset on which minimizing the Mixup loss can provably lead to learning a classifier that does not minimize the empirical loss on the data. On the other hand, we also give sufficient conditions for Mixup training to also minimize the original empirical risk. For generalization, we characterize the margin of a Mixup classifier, and use this to understand why the decision boundary of a Mixup classifier can adapt better to the full structure of the training data when compared to standard training. In contrast, we also show that, for a large class of linear models and linearly separable datasets, Mixup training leads to learning the same classifier as standard training.

Outlier-Robust Sparse Estimation via Non-Convex Optimization

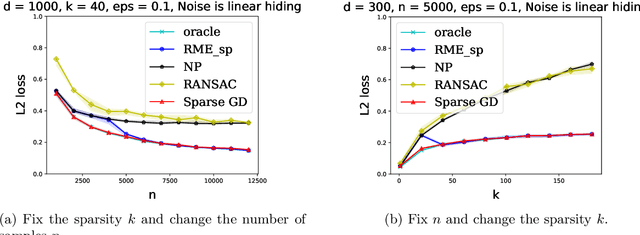
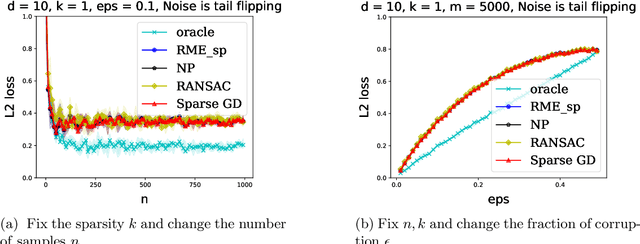
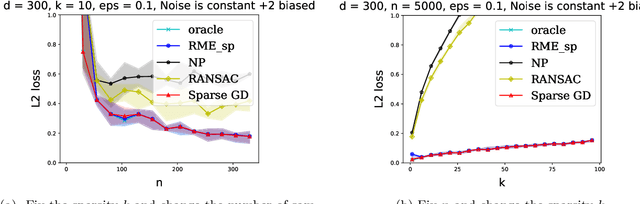
We explore the connection between outlier-robust high-dimensional statistics and non-convex optimization in the presence of sparsity constraints, with a focus on the fundamental tasks of robust sparse mean estimation and robust sparse PCA. We develop novel and simple optimization formulations for these problems such that any approximate stationary point of the associated optimization problem yields a near-optimal solution for the underlying robust estimation task. As a corollary, we obtain that any first-order method that efficiently converges to stationarity yields an efficient algorithm for these tasks. The obtained algorithms are simple, practical, and succeed under broader distributional assumptions compared to prior work.

Understanding Deflation Process in Over-parametrized Tensor Decomposition

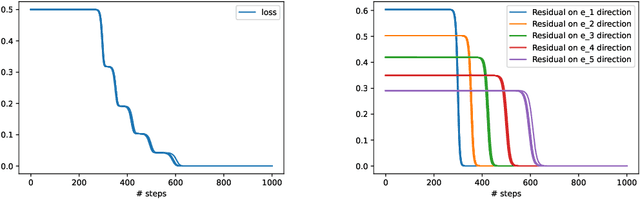
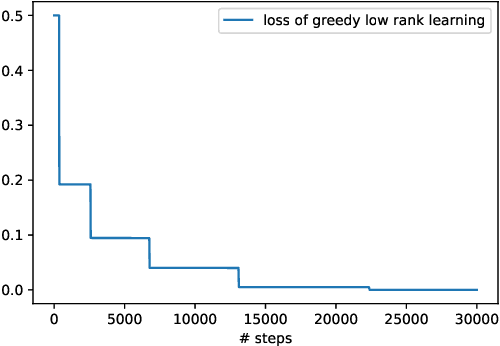
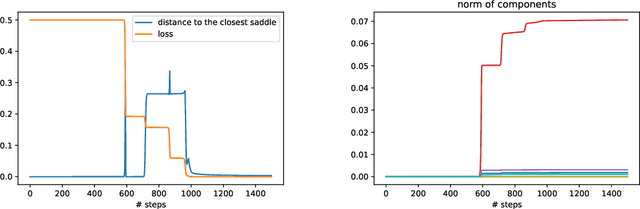
In this paper we study the training dynamics for gradient flow on over-parametrized tensor decomposition problems. Empirically, such training process often first fits larger components and then discovers smaller components, which is similar to a tensor deflation process that is commonly used in tensor decomposition algorithms. We prove that for orthogonally decomposable tensor, a slightly modified version of gradient flow would follow a tensor deflation process and recover all the tensor components. Our proof suggests that for orthogonal tensors, gradient flow dynamics works similarly as greedy low-rank learning in the matrix setting, which is a first step towards understanding the implicit regularization effect of over-parametrized models for low-rank tensors.

A Local Convergence Theory for Mildly Over-Parameterized Two-Layer Neural Network

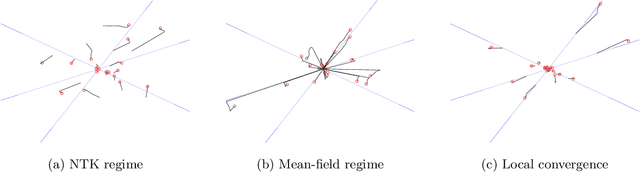
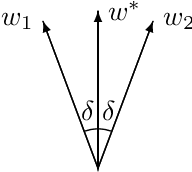
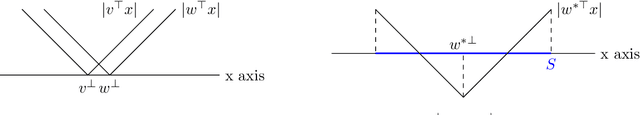
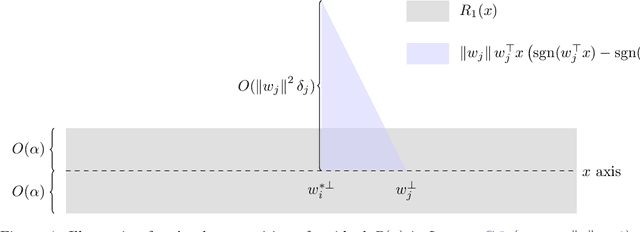
While over-parameterization is widely believed to be crucial for the success of optimization for the neural networks, most existing theories on over-parameterization do not fully explain the reason -- they either work in the Neural Tangent Kernel regime where neurons don't move much, or require an enormous number of neurons. In practice, when the data is generated using a teacher neural network, even mildly over-parameterized neural networks can achieve 0 loss and recover the directions of teacher neurons. In this paper we develop a local convergence theory for mildly over-parameterized two-layer neural net. We show that as long as the loss is already lower than a threshold (polynomial in relevant parameters), all student neurons in an over-parameterized two-layer neural network will converge to one of teacher neurons, and the loss will go to 0. Our result holds for any number of student neurons as long as it is at least as large as the number of teacher neurons, and our convergence rate is independent of the number of student neurons. A key component of our analysis is the new characterization of local optimization landscape -- we show the gradient satisfies a special case of Lojasiewicz property which is different from local strong convexity or PL conditions used in previous work.

Beyond Lazy Training for Over-parameterized Tensor Decomposition

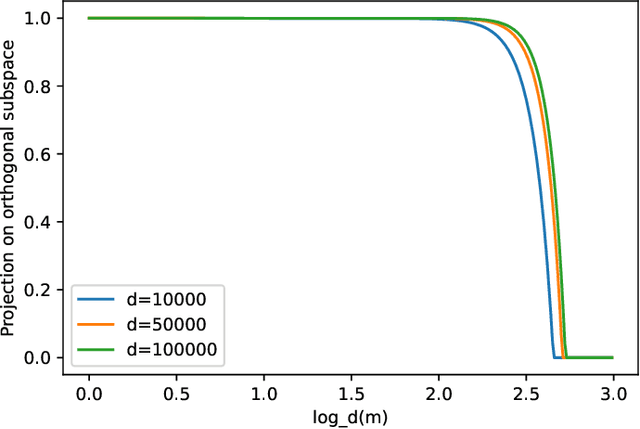
Over-parametrization is an important technique in training neural networks. In both theory and practice, training a larger network allows the optimization algorithm to avoid bad local optimal solutions. In this paper we study a closely related tensor decomposition problem: given an $l$-th order tensor in $(R^d)^{\otimes l}$ of rank $r$ (where $r\ll d$), can variants of gradient descent find a rank $m$ decomposition where $m > r$? We show that in a lazy training regime (similar to the NTK regime for neural networks) one needs at least $m = \Omega(d^{l-1})$, while a variant of gradient descent can find an approximate tensor when $m = O^*(r^{2.5l}\log d)$. Our results show that gradient descent on over-parametrized objective could go beyond the lazy training regime and utilize certain low-rank structure in the data.

Dissecting Hessian: Understanding Common Structure of Hessian in Neural Networks

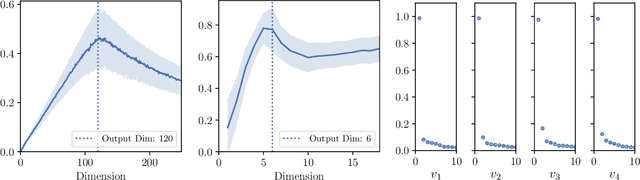
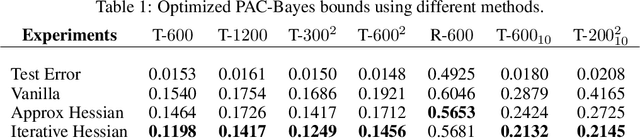
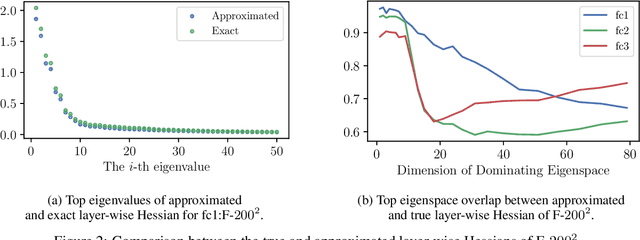
Hessian captures important properties of the deep neural network loss landscape. We observe that eigenvectors and eigenspaces of the layer-wise Hessian for neural network objective have several interesting structures -- top eigenspaces for different models have high overlap, and top eigenvectors form low rank matrices when they are reshaped into the same shape as the corresponding weight matrix. These structures, as well as the low rank structure of the Hessian observed in previous studies, can be explained by approximating the Hessian using Kronecker factorization. Our new understanding can also explain why some of these structures become weaker when the network is trained with batch normalization. Finally, we show that the Kronecker factorization can be combined with PAC-Bayes techniques to get better explicit generalization bounds.

Efficient sampling from the Bingham distribution

We give a algorithm for exact sampling from the Bingham distribution $p(x)\propto \exp(x^\top A x)$ on the sphere $\mathcal S^{d-1}$ with expected runtime of $\operatorname{poly}(d, \lambda_{\max}(A)-\lambda_{\min}(A))$. The algorithm is based on rejection sampling, where the proposal distribution is a polynomial approximation of the pdf, and can be sampled from by explicitly evaluating integrals of polynomials over the sphere. Our algorithm gives exact samples, assuming exact computation of an inverse function of a polynomial. This is in contrast with Markov Chain Monte Carlo algorithms, which are not known to enjoy rapid mixing on this problem, and only give approximate samples. As a direct application, we use this to sample from the posterior distribution of a rank-1 matrix inference problem in polynomial time.

Guarantees for Tuning the Step Size using a Learning-to-Learn Approach

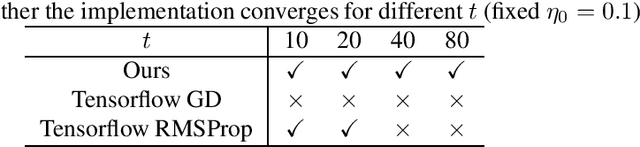
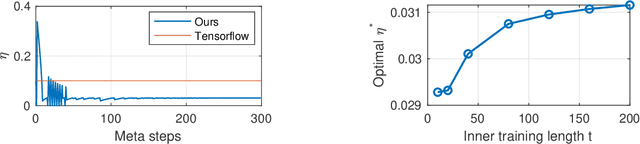
Learning-to-learn (using optimization algorithms to learn a new optimizer) has successfully trained efficient optimizers in practice. This approach relies on meta-gradient descent on a meta-objective based on the trajectory that the optimizer generates. However, there were few theoretical guarantees on how to avoid meta-gradient explosion/vanishing problems, or how to train an optimizer with good generalization performance. In this paper, we study the learning-to-learn approach on a simple problem of tuning the step size for quadratic loss. Our results show that although there is a way to design the meta-objective so that the meta-gradient remain polynomially bounded, computing the meta-gradient directly using backpropagation leads to numerical issues that look similar to gradient explosion/vanishing problems. We also characterize when it is necessary to compute the meta-objective on a separate validation set instead of the original training set. Finally, we verify our results empirically and show that a similar phenomenon appears even for more complicated learned optimizers parametrized by neural networks.